Revision as of 16:43, 4 December 2020

Application of Leibniz's Rule in Electrostatics

From what we've seen about the Feynman/Leibniz rule of integration, we now have an additional method of integrating that will be able to find us solutions for various complex integrals that would have been much more difficult to solve before. This, however, doesn't apply solely to the field of mathematics. Since many areas of study utilize the helpfulness of integration and calculating values through derivates, it can be assumed that they will also benefit a lot from the Feynman technique. Physics in particular has a lot of use for these concepts, with velocity and acceleration being important aspects of the field, and its use continues throughout the rest of the topics. For example, one of these topics is electrostatics, which deals with the idea of calculation charge on a particle.

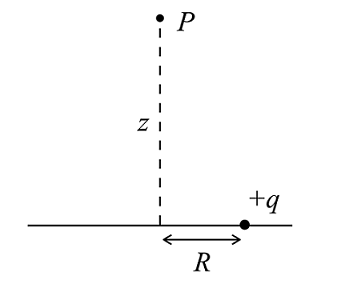
The simple equation for finding the charge would be

Back to Feynman Integrals