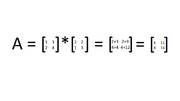| Line 6: | Line 6: | ||
# Introduction | # Introduction | ||
# The Basics | # The Basics | ||
| − | # Deeper Understanding | + | # Deeper Understanding |
| + | # Example | ||
# Applications | # Applications | ||
# References | # References | ||
| Line 12: | Line 13: | ||
Introduction: | Introduction: | ||
| − | Singular Value Decomposition has many names, such as factor analysis, empirical orthogonal function analysis, and principal component decomposition. In this discussion, I will refer to it as SVD. To put it simply, Singular Value Decomposition is decomposing a | + | Singular Value Decomposition has many names, such as factor analysis, empirical orthogonal function analysis, and principal component decomposition. In this discussion, I will refer to it as SVD. To put it simply, Singular Value Decomposition is decomposing a matrix into three parts so that it is easier to understand and transform. The three parts that it decomposes to can give more information about the original matrix and the relationships that its rows and columns have to one another. This has many applications in data science when displaying a set of information in a matrix. SVD is mainly used in linear algebra, but it can be understood in its most basic form as early as Calculus or even in Physics classes when breaking down vectors into components and projections. SVD was discovered by many different mathematicians in the late 1800s, namely Eugenio Beltrami and Camille Jordan, but would later become very important with the development of computers and big data. |
The Basics: | The Basics: | ||
| Line 22: | Line 23: | ||
[[File:Graphically.png|thumbnail]] | [[File:Graphically.png|thumbnail]] | ||
| − | + | Deeper Understanding: | |
| + | |||
| + | To dive deeper into what SVD does mathematically, one must understand eigenvalues and eigenvectors. Essentially, an eigenvalue is a scalar quantity that is used to linearly transform a vector or matrix. This is seen often in linear algebra and can be very important for engineering and physics to understand how objects behave. For further understanding of what eigenvalues truly are, see these references: | ||
| + | * https://mathworld.wolfram.com/Eigenvalue.html | ||
| + | * https://lpsa.swarthmore.edu/MtrxVibe/EigMat/MatrixEigen.html | ||
| + | * https://math.mit.edu/~gs/linearalgebra/ila0601.pdf | ||
| + | |||
| + | So, if we want to truly calculate the SVD, we need to used eigenvectors to find V and U from our given A. We know that the columns of V come from the eigenvectors A<sup>T</sup>A and the columns of U come from the eigenvectors of AA<sup>T</sup>. S indicates the sum of these matrices, where the values come from square-rooting the eigenvalues of V and U and go down in order from highest to lowest along the diagonal matrix for S. The website [http://web.mit.edu/course/other/be.400/OldFiles/www/SVD/Singular_Value_Decomposition.htm Singular Value Decomposition (SVD) tutorial] has a clear example on using eigenvectors and eigenvalues to find U, V, and S for a real matrix A. | ||
| + | |||
| + | Example: | ||
| + | |||
[[File:Moviedata.png|thumbnail|https://www.youtube.com/watch?v=P5mlg91as1c]] | [[File:Moviedata.png|thumbnail|https://www.youtube.com/watch?v=P5mlg91as1c]] | ||
To gain a better understanding of how we can use SVD, let’s look at an example from the video about Singular Value Decomposition from Stanford University. In the example, there is a data set of 7 people and 5 different movies that they watched. Each person rated each movie, and the matrix arranges this data to show who liked which movie. From the movie options, we can see that there were two main genres of movies watched- Romance and Sci-Fi. By taking the SVD to analyze this data, we find this output: | To gain a better understanding of how we can use SVD, let’s look at an example from the video about Singular Value Decomposition from Stanford University. In the example, there is a data set of 7 people and 5 different movies that they watched. Each person rated each movie, and the matrix arranges this data to show who liked which movie. From the movie options, we can see that there were two main genres of movies watched- Romance and Sci-Fi. By taking the SVD to analyze this data, we find this output: | ||
Revision as of 11:48, 4 December 2020
Singular Value Decomposition
Katie Wilson
Table of Contents:
- Introduction
- The Basics
- Deeper Understanding
- Example
- Applications
- References
Introduction:
Singular Value Decomposition has many names, such as factor analysis, empirical orthogonal function analysis, and principal component decomposition. In this discussion, I will refer to it as SVD. To put it simply, Singular Value Decomposition is decomposing a matrix into three parts so that it is easier to understand and transform. The three parts that it decomposes to can give more information about the original matrix and the relationships that its rows and columns have to one another. This has many applications in data science when displaying a set of information in a matrix. SVD is mainly used in linear algebra, but it can be understood in its most basic form as early as Calculus or even in Physics classes when breaking down vectors into components and projections. SVD was discovered by many different mathematicians in the late 1800s, namely Eugenio Beltrami and Camille Jordan, but would later become very important with the development of computers and big data.
The Basics:
Before we get into what SVD really means, it is important to understand some basic concepts. Firstly, SVD deals with matrices, which are a collection of values put into rows and columns. Matrices can be described by the number of rows (n) and columns (m) that they have in the form n x m, which is important to understand when performing operations on them. Matrices can be added, subtracted, multiplied, and divided just like functions, but the processes are a little different. For example, to multiply a matrix by another, you must take the dot product of the two. This is when you multiply each value in the row of the first matrix by each value in the column of the second matrix. For example:
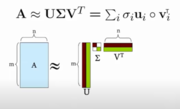
Additionally, to divide matrices, you are actually multiplying by the inverse. However, this is not as important when it comes to SVD. The main equation for SVD is A=USV^T, where: “A is an m × n matrix, U is an m × n orthogonal matrix, S is an n × n diagonal matrix, and V is an n × n orthogonal matrix,” (1). An orthogonal matrix is when the columns and rows are perpendicular unit vectors, and a diagonal matrix contains all values that are zero except in the diagonal line down from the top left to the bottom right. Additionally, in the equation, the ^T stands for “transpose” of the matrix which basically flips the original matrix. We know that U^TU and V^TV both give the identity matrix because U and V are orthogonal. Another way of viewing this equation is by looking at it graphically: (7)
Deeper Understanding:
To dive deeper into what SVD does mathematically, one must understand eigenvalues and eigenvectors. Essentially, an eigenvalue is a scalar quantity that is used to linearly transform a vector or matrix. This is seen often in linear algebra and can be very important for engineering and physics to understand how objects behave. For further understanding of what eigenvalues truly are, see these references:
- https://mathworld.wolfram.com/Eigenvalue.html
- https://lpsa.swarthmore.edu/MtrxVibe/EigMat/MatrixEigen.html
- https://math.mit.edu/~gs/linearalgebra/ila0601.pdf
So, if we want to truly calculate the SVD, we need to used eigenvectors to find V and U from our given A. We know that the columns of V come from the eigenvectors ATA and the columns of U come from the eigenvectors of AAT. S indicates the sum of these matrices, where the values come from square-rooting the eigenvalues of V and U and go down in order from highest to lowest along the diagonal matrix for S. The website Singular Value Decomposition (SVD) tutorial has a clear example on using eigenvectors and eigenvalues to find U, V, and S for a real matrix A.
Example:
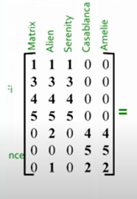
To gain a better understanding of how we can use SVD, let’s look at an example from the video about Singular Value Decomposition from Stanford University. In the example, there is a data set of 7 people and 5 different movies that they watched. Each person rated each movie, and the matrix arranges this data to show who liked which movie. From the movie options, we can see that there were two main genres of movies watched- Romance and Sci-Fi. By taking the SVD to analyze this data, we find this output:
The first matrix U represents how each person responded to the different genres, where the first column represents the Sci-Fi genre and the second relates to the Romance concept. We can see that the first four people responded more strongly to the Sci-Fi genre as there is a higher correlation in that matrix, while the last three more towards Romance. The second diagonal matrix S shows the strength of each genre, or how many people liked it. So, Sci-Fi was the most popular genre because it has a strength of 12.4. The last value (1.3) shows that the third column does not have a large strength on the data, so it does not represent a significant genre and we can ignore it. The last matrix V relates to how strongly each movie corresponds to the two concepts. From this, we can see that “Casablanca” and “Amelie” are more strongly related to romance, while the other three movies are closer to the Sci-Fi category. So, by using SVD we can learn more about each individual person and their preferences for the movies as well as how the movies relate to each genre presented.
References:
- https://blog.statsbot.co/singular-value-decomposition-tutorial-52c695315254
- https://towardsdatascience.com/svd-8c2f72e264f
- https://towardsdatascience.com/understanding-singular-value-decomposition-and-its-application-in-data-science-388a54be95d
- http://web.mit.edu/course/other/be.400/OldFiles/www/SVD/Singular_Value_Decomposition.htm
- https://mathinsight.org/matrix_transpose
- https://www.youtube.com/watch?v=mBcLRGuAFUk
- https://www.youtube.com/watch?v=P5mlg91as1c