| (14 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
This makes sense logically, as our brains classify different phonemes and speech to be different ranges of frequencies in order to process speech signals, otherwise all sounds would mean the same thing! | This makes sense logically, as our brains classify different phonemes and speech to be different ranges of frequencies in order to process speech signals, otherwise all sounds would mean the same thing! | ||
| − | In order for our brains to have universally recognized phonemes, it follows that a phoneme | + | In order for our brains to have universally recognized phonemes, it follows that a phoneme has roughly the same formant frequencies for everyone, e.g. "you" sounds like "yoo" for everyone. |
Interestingly enough, this implies that the variations between individual pitch caused by differences in vocal cord size (which affects the frequency of the vocal folds when voicing signals) does NOT affect the resonant frequencies of the vocal tract. | Interestingly enough, this implies that the variations between individual pitch caused by differences in vocal cord size (which affects the frequency of the vocal folds when voicing signals) does NOT affect the resonant frequencies of the vocal tract. | ||
Think of the vocal tract as a garden hose with a variable-spray nozzle. The water pressure/flow is your vocal cords applying an input to your nozzle, or vocal tract. Your nozzle (vocal tract) then selects which spray settings it wants to shape the water flow into before it spreads out from the end of the hose, which is seen the same by both yourself and the outside world: the same as your speech! | Think of the vocal tract as a garden hose with a variable-spray nozzle. The water pressure/flow is your vocal cords applying an input to your nozzle, or vocal tract. Your nozzle (vocal tract) then selects which spray settings it wants to shape the water flow into before it spreads out from the end of the hose, which is seen the same by both yourself and the outside world: the same as your speech! | ||
| + | |||
| + | Keeping these concepts in mind, we will use a spectogram-based approach to identify formant frequencies in my speech and compare them to known formant frequencies to both demonstrate how to identify formant frequencies, and to show that formant frequencies are universal. | ||
----- | ----- | ||
| Line 40: | Line 42: | ||
# Plot time-domain representations of voiced phonemes | # Plot time-domain representations of voiced phonemes | ||
# Create Spectographic Representations of each signal by applying a shifting N-point DFT window along the length of the input signal and converting the resulting DFT into a column of an output matrix (wideband spectogram) | # Create Spectographic Representations of each signal by applying a shifting N-point DFT window along the length of the input signal and converting the resulting DFT into a column of an output matrix (wideband spectogram) | ||
| − | # Identify formant frequencies F1 and F2 at the beginning and end of speech | + | # Identify formant frequencies F1 and F2 and record their respective frequencies at the beginning and end of speech (heads and tails of formant "streaks") |
# Compare formant frequencies of custom signals to commonly accepted values of voiced phonemes | # Compare formant frequencies of custom signals to commonly accepted values of voiced phonemes | ||
----- | ----- | ||
==Matlab Code== | ==Matlab Code== | ||
| − | 1#- DFT Window Function: | + | 1#- DFT Window Function: This allows us to create the column vectors of our spectogram by performing multiple DFTs across the signal. |
function [X] = DFTwin(x,L,m,N) | function [X] = DFTwin(x,L,m,N) | ||
| Line 57: | Line 59: | ||
end | end | ||
| − | 2#- Spectogram Function (16kHz compatibility): | + | 2#- Spectogram Function (16kHz compatibility): This allows us to generate our spectogram by piecing together our DFTs using a chosen window length L, window overlap value, and value of N for our N-pt dft. Note that These values can be varied to affect the final appearance of the spectogram, but the values below were chosen/tweaked to balance ease of viewing, computation time, and signal detail. |
function [A] = Specgm2(x,L,overlap,N) | function [A] = Specgm2(x,L,overlap,N) | ||
| Line 82: | Line 84: | ||
end | end | ||
| − | 3#- Main Project Script: [[ | + | '''Crude Diagram of How the Spectogram is Generated:''' |
| + | |||
| + | [[Image:crudeSpectogram.png]] | ||
| + | |||
| + | 3#- Main Project Script: | ||
| + | %{ | ||
| + | ECE438 Bonus Project - Brandon Henman | ||
| + | Date: 11/15/2019 | ||
| + | Note: Code takes a while to run on slower computers due to the sampling | ||
| + | rate & the multiple signals being processed. | ||
| + | %} | ||
| + | |||
| + | format rat %fractions are better than decimals | ||
| + | clear %clear vars | ||
| + | close all %refresh all figures | ||
| + | %Load Audio Signals, 16kHz Sampling Rate | ||
| + | audio_a = transpose(audioread('vowels_voiced_a.wav')); | ||
| + | audio_e = transpose(audioread('vowels_voiced_e.wav')); | ||
| + | audio_i = transpose(audioread('vowels_voiced_i.wav')); | ||
| + | audio_o = transpose(audioread('vowels_voiced_o.wav')); | ||
| + | audio_u = transpose(audioread('vowels_voiced_u.wav')); | ||
| + | %convert to single-channel audio (2-channel) | ||
| + | audio_a = audio_a(1,:); | ||
| + | audio_e = audio_e(1,:); | ||
| + | audio_i = audio_i(1,:); | ||
| + | audio_o = audio_o(1,:); | ||
| + | audio_u = audio_u(1,:); | ||
| + | %Play Audio Signals | ||
| + | %sound(audio_a,16000); | ||
| + | %sound(audio_e,16000); | ||
| + | %sound(audio_i,16000); | ||
| + | %sound(audio_o,16000); | ||
| + | %sound(audio_u,16000); | ||
| + | |||
| + | %time plotting vectors | ||
| + | fs = 16000; %sampling frequency | ||
| + | N = 1024; %DFT samples | ||
| + | ta = 1:1:length(audio_a); | ||
| + | ta = ta./ fs; | ||
| + | te = 1:1:length(audio_e); | ||
| + | te = te./ fs; | ||
| + | ti = 1:1:length(audio_i); | ||
| + | ti = ti./ fs; | ||
| + | to = 1:1:length(audio_o); | ||
| + | to = to./ fs; | ||
| + | tu = 1:1:length(audio_u); | ||
| + | tu = tu./ fs; | ||
| + | |||
| + | %speech signal plots | ||
| + | figure(1) | ||
| + | subplot(5,1,1) | ||
| + | plot(ta,audio_a) | ||
| + | xlabel('t, sec') | ||
| + | ylabel('Amplitude') | ||
| + | title('Speech: "a"') | ||
| + | xlim([1.05 1.35]) | ||
| + | subplot(5,1,2) | ||
| + | plot(te,audio_e) | ||
| + | xlabel('t, sec') | ||
| + | ylabel('Amplitude') | ||
| + | title('Speech: "e"') | ||
| + | xlim([1.1 1.45]) | ||
| + | subplot(5,1,3) | ||
| + | plot(ti,audio_i) | ||
| + | xlabel('t, sec') | ||
| + | ylabel('Amplitude') | ||
| + | title('Speech: "i"') | ||
| + | xlim([1 1.35]) | ||
| + | subplot(5,1,4) | ||
| + | plot(to,audio_o) | ||
| + | xlabel('t, sec') | ||
| + | ylabel('Amplitude') | ||
| + | title('Speech: "o"') | ||
| + | xlim([1 1.3]) | ||
| + | subplot(5,1,5) | ||
| + | plot(tu,audio_u) | ||
| + | xlabel('t, sec') | ||
| + | ylabel('Amplitude') | ||
| + | title('Speech: "u"') | ||
| + | xlim([1.1 1.45]) | ||
| + | |||
| + | %plotting spectograms | ||
| + | |||
| + | %wideband spec a | ||
| + | figure(2) | ||
| + | Specgm2(audio_a,100,80,N); | ||
| + | xlabel('t') | ||
| + | ylabel('Hz') | ||
| + | xlim([1 1.5]) | ||
| + | title('Wideband Spectogram of "a"') | ||
| + | |||
| + | %wideband spec e | ||
| + | figure(3) | ||
| + | Specgm2(audio_e,100,80,N); | ||
| + | xlabel('t') | ||
| + | ylabel('Hz') | ||
| + | xlim([1.07 1.56]) | ||
| + | title('Wideband Spectogram of "e"') | ||
| + | |||
| + | %wideband spec i | ||
| + | figure(4) | ||
| + | Specgm2(audio_i,100,80,N); | ||
| + | xlabel('t') | ||
| + | ylabel('Hz') | ||
| + | xlim([0.98 1.49]) | ||
| + | title('Wideband Spectogram of "i"') | ||
| + | |||
| + | %wideband spec o | ||
| + | figure(5) | ||
| + | Specgm2(audio_o,100,80,N); | ||
| + | xlabel('t') | ||
| + | ylabel('Hz') | ||
| + | xlim([0.99 1.35]) | ||
| + | title('Wideband Spectogram of "o"') | ||
| + | |||
| + | %wideband spec u | ||
| + | figure(6) | ||
| + | Specgm2(audio_u,100,80,N); | ||
| + | xlabel('t') | ||
| + | ylabel('Hz') | ||
| + | xlim([1.05 1.48]) | ||
| + | title('Wideband Spectogram of "u"') | ||
| + | |||
| + | |||
----- | ----- | ||
==Spectogram Results & Formant Analysis== | ==Spectogram Results & Formant Analysis== | ||
| − | Wideband Spectogram of A: | + | Due to the relatively short window size used to make the wideband spectogram, it is straightforward to identify high-magnitude frequencies across duration of the signal. Additionally, the short window size provides more detail of how the frequency of the signal changes over time, at the cost of less accuracy (a wider formant streak/band) when trying to determine the exact frequency of formants. Here, we approximate formant frequencies to be the approximate center(s) of each formant "streak" on the spectogram, which correspond to resonances in the vocal tract. |
| + | |||
| + | Formant frequencies F1 and F2 are the first two streaks (resonances) starting from the bottom of the plot, and are measured near the head and tail ends of each formant "streak" to observe how the formant frequencies shift over the pronunciation of an english vowel. | ||
| + | |||
| + | Note that each spectogram has a streak near the zero-frequency: this is not a speech formant, but rather noise from the input signals and noise due to windowing effects of the spectogram. | ||
| + | |||
| + | '''Wideband Spectogram of A:''' | ||
| + | |||
| + | Note the formant frequencies: | ||
| + | |||
| + | - F1: 563 -> 438 Hz | ||
| + | |||
| + | - F2: 1785 -> 2004 Hz | ||
[[Image:WbSpec_a.png]] | [[Image:WbSpec_a.png]] | ||
| − | Wideband Spectogram of E: | + | '''Wideband Spectogram of E:''' |
| + | |||
| + | Note the formant frequencies: | ||
| + | |||
| + | - F1: 391 -> 344 Hz | ||
| + | |||
| + | - F2: 1988 -> 2207 Hz | ||
[[Image:WbSpec_e.png]] | [[Image:WbSpec_e.png]] | ||
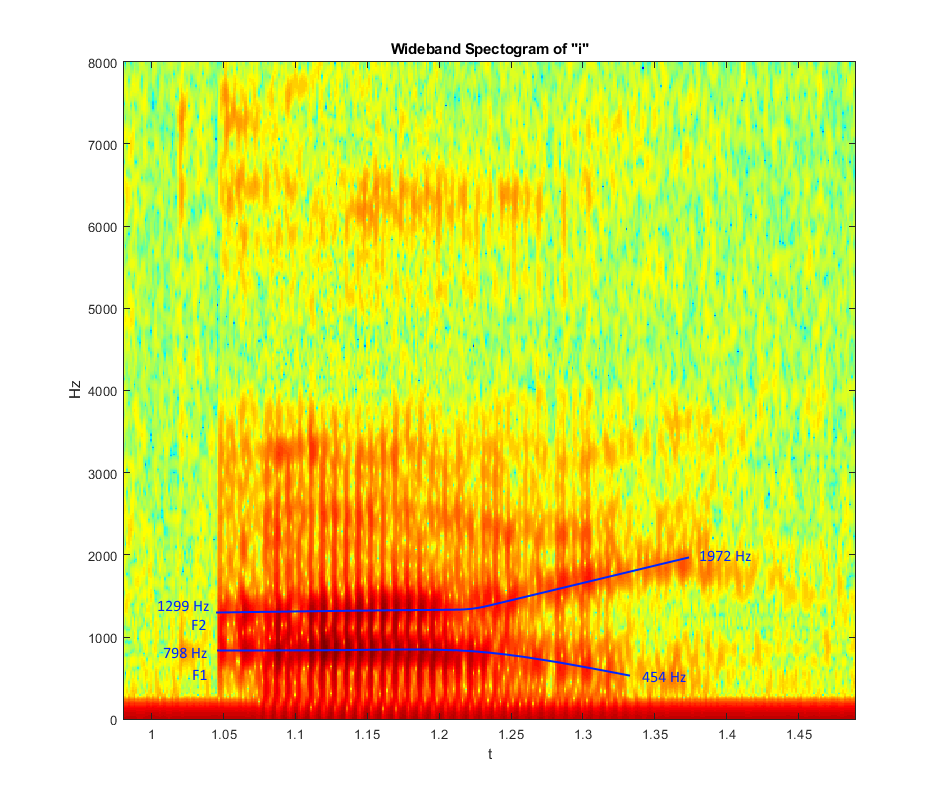
| − | Wideband Spectogram of I: | + | '''Wideband Spectogram of I:''' |
| + | |||
| + | Note the formant frequencies: | ||
| + | |||
| + | - F1: 798 -> 454 Hz | ||
| + | |||
| + | - F2: 1299 -> 1972 Hz | ||
[[Image:WbSpec_i.png]] | [[Image:WbSpec_i.png]] | ||
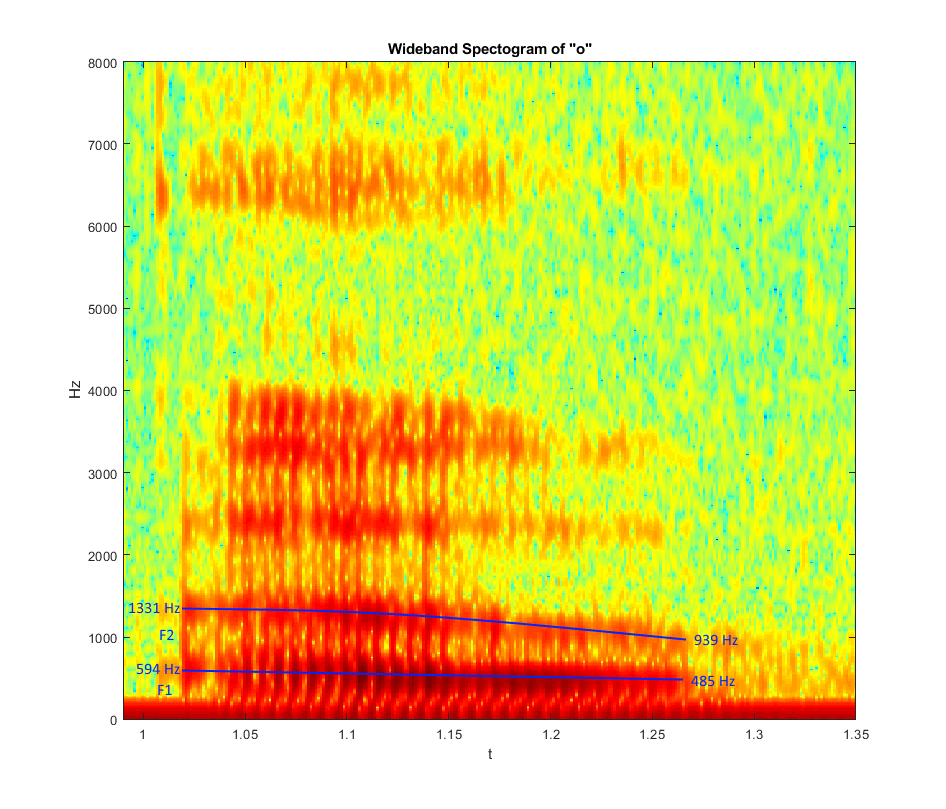
| − | Wideband Spectogram of O: | + | '''Wideband Spectogram of O:''' |
| + | |||
| + | Note the formant frequencies: | ||
| + | |||
| + | - F1: 594 -> 485 Hz | ||
| + | |||
| + | - F2: 1331 -> 939 Hz | ||
[[Image:WbSpec_o.png]] | [[Image:WbSpec_o.png]] | ||
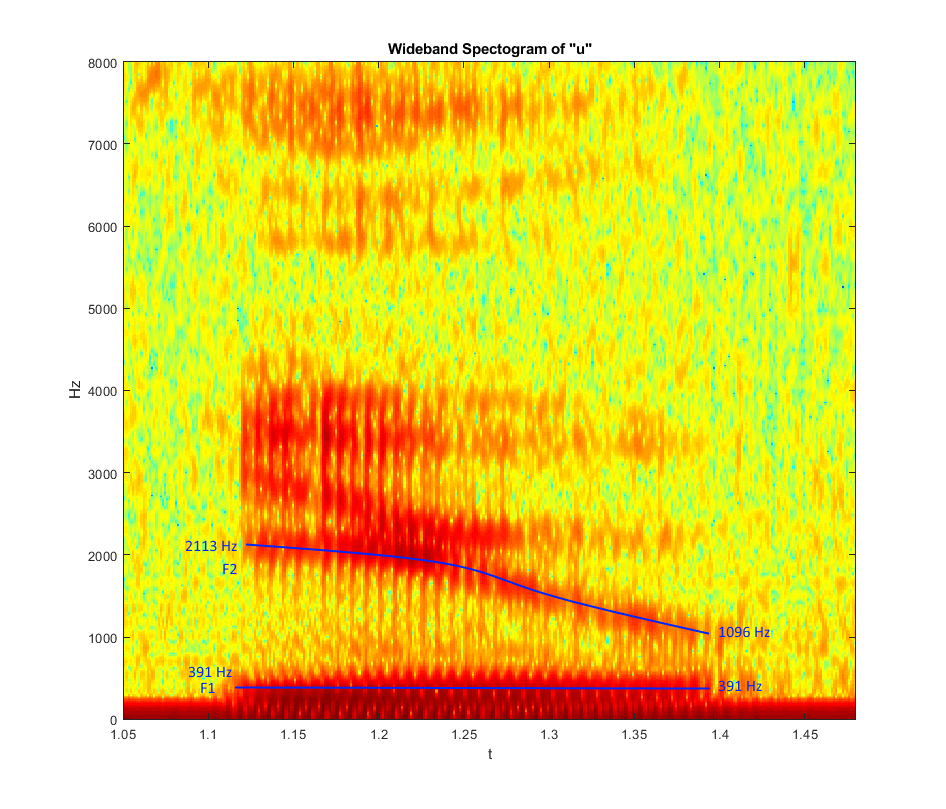
| − | Wideband Spectogram of U: | + | '''Wideband Spectogram of U:''' |
| + | |||
| + | Note the formant frequencies: | ||
| + | |||
| + | - F1: 391 -> 391 Hz | ||
| + | |||
| + | - F2: 2113 -> 1096 Hz | ||
[[Image:WbSpec_u.png]] | [[Image:WbSpec_u.png]] | ||
| + | |||
| + | |||
| + | '''Comparing to Known Formants:''' | ||
| + | |||
| + | Now we will compare the results of english phonemes with the IPA vowel frequencies. A link with sounds to compare yourself is here: [https://en.wikipedia.org/wiki/IPA_vowel_chart_with_audio [IPA Vowel Chart<nowiki>]</nowiki>] | ||
| + | |||
| + | Comparing both the sounds from the audio reference and the IPA chart on: [https://en.wikipedia.org/wiki/Formant IPA Formant Frequency Chart] | ||
| + | |||
| + | -The pronunciation of "a" starts at IPA "œ" and shifts close to IPA "e" | ||
| + | |||
| + | -The pronunciation of "e" starts similar to IPA "ø" and shifts close to IPA "e" | ||
| + | |||
| + | -The pronunciation of "i" starts similar to IPA "ɶ" (different from "œ") and shifts close to IPA "ø" | ||
| + | |||
| + | -The pronunciation of "o" starts similar to IPA "ʌ" and shifts close to IPA "ɔ" | ||
| + | |||
| + | -The pronunciation of "u" starts between IPA "ø & e" and shifts to IPA "ʊ" (not shown on plot) | ||
| + | |||
| + | Note that many IPA formant frequencies are not shown on the chart, so sounds are matched to similar-frequency IPA-chart formant frequencies so the numerical proximity can be seen. Carefully listening to the recorded sounds provided in this project do yield similar sounds that sometimes match some sounds not on the chart, but in the IPA audio library in the provided link. | ||
----- | ----- | ||
==Summary== | ==Summary== | ||
| + | We were able to identify and compare formant frequencies in pronounced english vowels with relative ease and accuracy, though several sources of error included the sampling rate of the audio, the resolution of the spectogram, and the approximation of spectogram formant frequencies for the sake of comparison to well-known IPA vowel sounds. | ||
| + | |||
| + | |||
| + | In conclusion, there is some variance when comparing english vowel pronunciations to more well-known frequencies, though through approximation and training such phonemes could be easily identified, particularly through machine learning and many training sets of test audio. | ||
| + | |||
| + | Ultimately, gathering many sets of english vowel pronunciations would (and do) yield similar-frequency results with slight variation. Through comparing the results to the IPA vowels we can confirm that similar sounds across small segments of time share similar resonant frequencies when voiced, even if the complete signal is of different composition. | ||
| + | |||
| + | This implies that speech could be sampled at a very high rate to capture smaller windows of time, which could be used to analyze the shifts in formant frequencies in real-time to perform speech recognition using FFT methods. | ||
----- | ----- | ||
| + | ==References== | ||
| + | - Lecture Notes for ECE438. F19 ed., 2019. | ||
| + | |||
| + | - ECE438 Lab #9: Speech Processing | ||
| + | |||
| + | -https://en.wikipedia.org/wiki/Formant | ||
| + | |||
| + | -https://en.wikipedia.org/wiki/IPA_vowel_chart_with_audio | ||
Latest revision as of 09:53, 28 November 2019
Contents
Formant Analysis Using Wideband Spectographic Representation
By user:BJH (Brandon Henman)
Topic Background
Like most systems in the real world, the human vocal tract can be broken down and modeled as a system that takes real inputs (vibration of vocal cords) and transforms them (via the vocal tract) into real outputs (human speech).
The vocal system itself resonates certain frequencies, called formant frequencies, depending on how a person changes the shape of their vocal tract in order to pronounce certain phonemes, or "building blocks" of sounds.
This makes sense logically, as our brains classify different phonemes and speech to be different ranges of frequencies in order to process speech signals, otherwise all sounds would mean the same thing!
In order for our brains to have universally recognized phonemes, it follows that a phoneme has roughly the same formant frequencies for everyone, e.g. "you" sounds like "yoo" for everyone.
Interestingly enough, this implies that the variations between individual pitch caused by differences in vocal cord size (which affects the frequency of the vocal folds when voicing signals) does NOT affect the resonant frequencies of the vocal tract.
Think of the vocal tract as a garden hose with a variable-spray nozzle. The water pressure/flow is your vocal cords applying an input to your nozzle, or vocal tract. Your nozzle (vocal tract) then selects which spray settings it wants to shape the water flow into before it spreads out from the end of the hose, which is seen the same by both yourself and the outside world: the same as your speech!
Keeping these concepts in mind, we will use a spectogram-based approach to identify formant frequencies in my speech and compare them to known formant frequencies to both demonstrate how to identify formant frequencies, and to show that formant frequencies are universal.
Audio Files
Here are some examples of voiced phonemes that will be analyzed for their formant frequencies:
-Custom-recorded, 16kHz sampling rate
Me saying "a" :Media:Vowels_voiced_a.wav ("ay")
Me saying "e" :Media:Vowels_voiced_e.wav ("ee")
Me saying "i" :Media:Vowels_voiced_i.wav ("eye")
Me saying "o" :Media:Vowels_voiced_o.wav ("oh")
Me saying "u" :Media:Vowels_voiced_u.wav ("yoo")
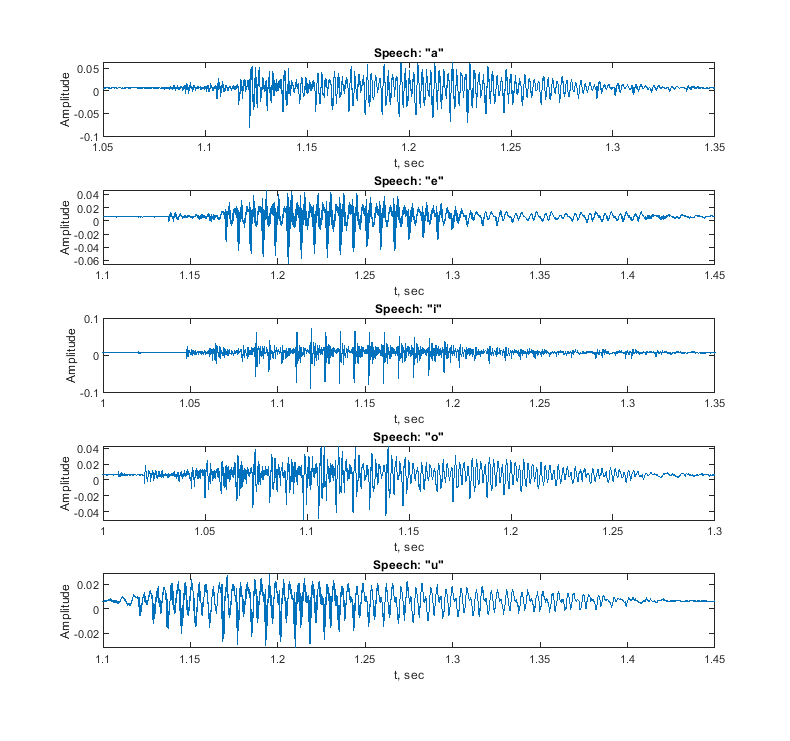
Time Domain Representation of Recorded Signals:
Methodology
- Convert the audio to single-channel
- Plot time-domain representations of voiced phonemes
- Create Spectographic Representations of each signal by applying a shifting N-point DFT window along the length of the input signal and converting the resulting DFT into a column of an output matrix (wideband spectogram)
- Identify formant frequencies F1 and F2 and record their respective frequencies at the beginning and end of speech (heads and tails of formant "streaks")
- Compare formant frequencies of custom signals to commonly accepted values of voiced phonemes
Matlab Code
1#- DFT Window Function: This allows us to create the column vectors of our spectogram by performing multiple DFTs across the signal.
function [X] = DFTwin(x,L,m,N)
%DFTwin computes the DFT of a windowed length L segment of vector x
window = hamming(L); %hamming window of desired length L
x1 = x(m:length(window)+m); %segment of x we want to DFT
signal = zeros(1,L);
for z =1:1:length(window)
signal(z) = x1(z) .* window(z);
end
X = fft(signal,N);
end
2#- Spectogram Function (16kHz compatibility): This allows us to generate our spectogram by piecing together our DFTs using a chosen window length L, window overlap value, and value of N for our N-pt dft. Note that These values can be varied to affect the final appearance of the spectogram, but the values below were chosen/tweaked to balance ease of viewing, computation time, and signal detail.
function [A] = Specgm2(x,L,overlap,N)
%Specgm creates a spectogram using DFTwin via a matrix of windowed DFTs
%create a matrix
for n = 1:1:length(x)
m = (((n-1) * L) - ((n-1) *overlap)) + 1;
if ((m+L) > length(x)) %if m + length of window exceeds the signal bounds
break
end
A(:,n) = transpose(DFTwin(x,L,m,N));
end
for z = 1:1:(N/2)
A(1,:) = []; %clear half of the matrix
end
A = 20*log10(abs(A)); %convert to dB
A = flip(A);
[l,k] = size(A); %#columns and rows in matrix A
y1 = 0:(1/(length(l))):8000 - (1/(length(k))); %0 to 8kHz
x1 = 0:(1/16000):length(x)/16000; %16kHz sampling rate
imagesc(x1,y1,A); %define x and y time/freq. vectors to plot
colormap(jet)
axis xy
end
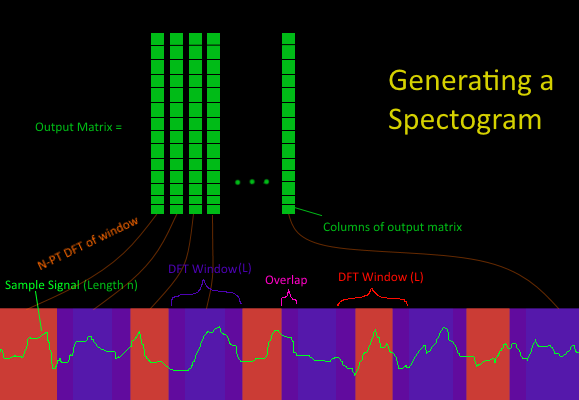
Crude Diagram of How the Spectogram is Generated:
3#- Main Project Script:
%{
ECE438 Bonus Project - Brandon Henman
Date: 11/15/2019
Note: Code takes a while to run on slower computers due to the sampling
rate & the multiple signals being processed.
%}
format rat %fractions are better than decimals
clear %clear vars
close all %refresh all figures
%Load Audio Signals, 16kHz Sampling Rate
audio_a = transpose(audioread('vowels_voiced_a.wav'));
audio_e = transpose(audioread('vowels_voiced_e.wav'));
audio_i = transpose(audioread('vowels_voiced_i.wav'));
audio_o = transpose(audioread('vowels_voiced_o.wav'));
audio_u = transpose(audioread('vowels_voiced_u.wav'));
%convert to single-channel audio (2-channel)
audio_a = audio_a(1,:);
audio_e = audio_e(1,:);
audio_i = audio_i(1,:);
audio_o = audio_o(1,:);
audio_u = audio_u(1,:);
%Play Audio Signals
%sound(audio_a,16000);
%sound(audio_e,16000);
%sound(audio_i,16000);
%sound(audio_o,16000);
%sound(audio_u,16000);
%time plotting vectors fs = 16000; %sampling frequency N = 1024; %DFT samples ta = 1:1:length(audio_a); ta = ta./ fs; te = 1:1:length(audio_e); te = te./ fs; ti = 1:1:length(audio_i); ti = ti./ fs; to = 1:1:length(audio_o); to = to./ fs; tu = 1:1:length(audio_u); tu = tu./ fs;
%speech signal plots
figure(1)
subplot(5,1,1)
plot(ta,audio_a)
xlabel('t, sec')
ylabel('Amplitude')
title('Speech: "a"')
xlim([1.05 1.35])
subplot(5,1,2)
plot(te,audio_e)
xlabel('t, sec')
ylabel('Amplitude')
title('Speech: "e"')
xlim([1.1 1.45])
subplot(5,1,3)
plot(ti,audio_i)
xlabel('t, sec')
ylabel('Amplitude')
title('Speech: "i"')
xlim([1 1.35])
subplot(5,1,4)
plot(to,audio_o)
xlabel('t, sec')
ylabel('Amplitude')
title('Speech: "o"')
xlim([1 1.3])
subplot(5,1,5)
plot(tu,audio_u)
xlabel('t, sec')
ylabel('Amplitude')
title('Speech: "u"')
xlim([1.1 1.45])
%plotting spectograms
%wideband spec a
figure(2)
Specgm2(audio_a,100,80,N);
xlabel('t')
ylabel('Hz')
xlim([1 1.5])
title('Wideband Spectogram of "a"')
%wideband spec e
figure(3)
Specgm2(audio_e,100,80,N);
xlabel('t')
ylabel('Hz')
xlim([1.07 1.56])
title('Wideband Spectogram of "e"')
%wideband spec i
figure(4)
Specgm2(audio_i,100,80,N);
xlabel('t')
ylabel('Hz')
xlim([0.98 1.49])
title('Wideband Spectogram of "i"')
%wideband spec o
figure(5)
Specgm2(audio_o,100,80,N);
xlabel('t')
ylabel('Hz')
xlim([0.99 1.35])
title('Wideband Spectogram of "o"')
%wideband spec u
figure(6)
Specgm2(audio_u,100,80,N);
xlabel('t')
ylabel('Hz')
xlim([1.05 1.48])
title('Wideband Spectogram of "u"')
Spectogram Results & Formant Analysis
Due to the relatively short window size used to make the wideband spectogram, it is straightforward to identify high-magnitude frequencies across duration of the signal. Additionally, the short window size provides more detail of how the frequency of the signal changes over time, at the cost of less accuracy (a wider formant streak/band) when trying to determine the exact frequency of formants. Here, we approximate formant frequencies to be the approximate center(s) of each formant "streak" on the spectogram, which correspond to resonances in the vocal tract.
Formant frequencies F1 and F2 are the first two streaks (resonances) starting from the bottom of the plot, and are measured near the head and tail ends of each formant "streak" to observe how the formant frequencies shift over the pronunciation of an english vowel.
Note that each spectogram has a streak near the zero-frequency: this is not a speech formant, but rather noise from the input signals and noise due to windowing effects of the spectogram.
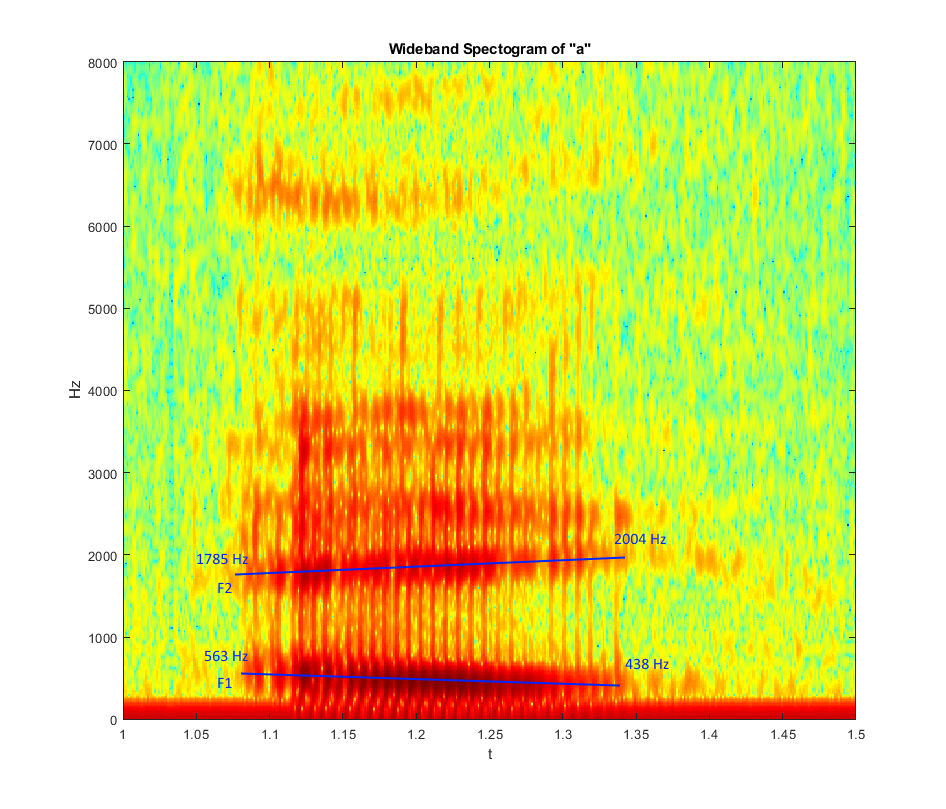
Wideband Spectogram of A:
Note the formant frequencies:
- F1: 563 -> 438 Hz
- F2: 1785 -> 2004 Hz
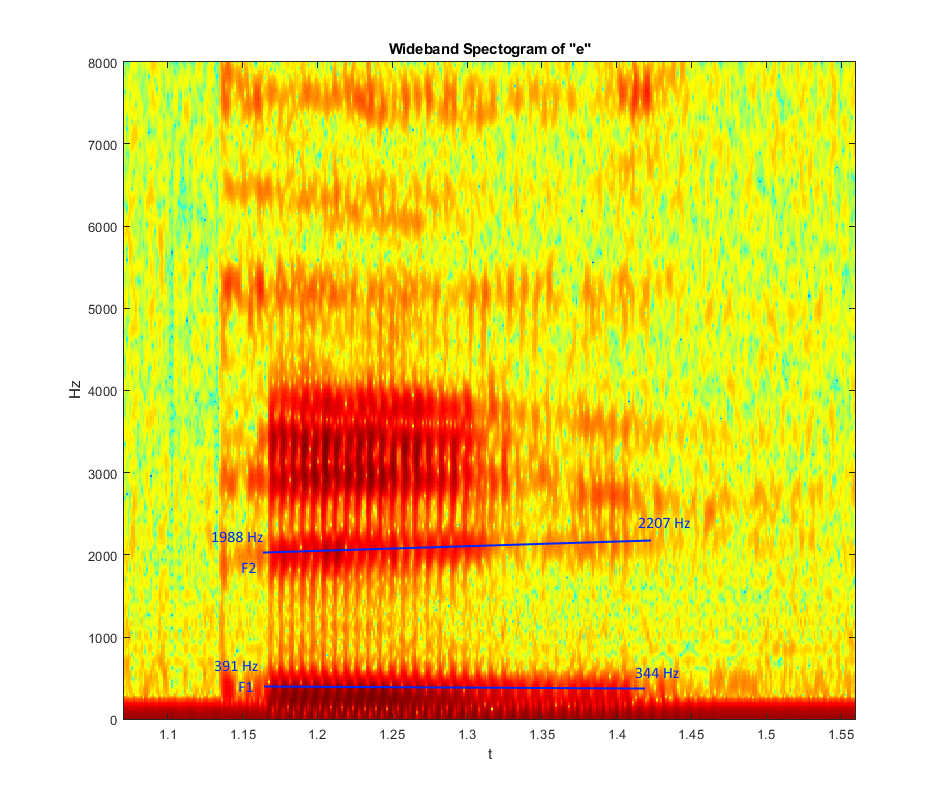
Wideband Spectogram of E:
Note the formant frequencies:
- F1: 391 -> 344 Hz
- F2: 1988 -> 2207 Hz
Wideband Spectogram of I:
Note the formant frequencies:
- F1: 798 -> 454 Hz
- F2: 1299 -> 1972 Hz
Wideband Spectogram of O:
Note the formant frequencies:
- F1: 594 -> 485 Hz
- F2: 1331 -> 939 Hz
Wideband Spectogram of U:
Note the formant frequencies:
- F1: 391 -> 391 Hz
- F2: 2113 -> 1096 Hz
Comparing to Known Formants:
Now we will compare the results of english phonemes with the IPA vowel frequencies. A link with sounds to compare yourself is here: [IPA Vowel Chart]
Comparing both the sounds from the audio reference and the IPA chart on: IPA Formant Frequency Chart
-The pronunciation of "a" starts at IPA "œ" and shifts close to IPA "e"
-The pronunciation of "e" starts similar to IPA "ø" and shifts close to IPA "e"
-The pronunciation of "i" starts similar to IPA "ɶ" (different from "œ") and shifts close to IPA "ø"
-The pronunciation of "o" starts similar to IPA "ʌ" and shifts close to IPA "ɔ"
-The pronunciation of "u" starts between IPA "ø & e" and shifts to IPA "ʊ" (not shown on plot)
Note that many IPA formant frequencies are not shown on the chart, so sounds are matched to similar-frequency IPA-chart formant frequencies so the numerical proximity can be seen. Carefully listening to the recorded sounds provided in this project do yield similar sounds that sometimes match some sounds not on the chart, but in the IPA audio library in the provided link.
Summary
We were able to identify and compare formant frequencies in pronounced english vowels with relative ease and accuracy, though several sources of error included the sampling rate of the audio, the resolution of the spectogram, and the approximation of spectogram formant frequencies for the sake of comparison to well-known IPA vowel sounds.
In conclusion, there is some variance when comparing english vowel pronunciations to more well-known frequencies, though through approximation and training such phonemes could be easily identified, particularly through machine learning and many training sets of test audio.
Ultimately, gathering many sets of english vowel pronunciations would (and do) yield similar-frequency results with slight variation. Through comparing the results to the IPA vowels we can confirm that similar sounds across small segments of time share similar resonant frequencies when voiced, even if the complete signal is of different composition.
This implies that speech could be sampled at a very high rate to capture smaller windows of time, which could be used to analyze the shifts in formant frequencies in real-time to perform speech recognition using FFT methods.
References
- Lecture Notes for ECE438. F19 ed., 2019.
- ECE438 Lab #9: Speech Processing