(add solution of question 1) |
(finish_ac1-2007_1) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 23: | Line 23: | ||
1. (10 pts) Find the transfer function <math> X(s)/U(s) </math> of the block diagram, shown in Figure 1. <br/> | 1. (10 pts) Find the transfer function <math> X(s)/U(s) </math> of the block diagram, shown in Figure 1. <br/> | ||
<center><math> X(s)/U(s)= ? </math></center><br/> | <center><math> X(s)/U(s)= ? </math></center><br/> | ||
| − | + | <center> https://www.projectrhea.org/rhea/dropbox_/40c5d9059656d63a4b7544531047c681/Chang534_f1.png </center><br/> | |
| − | Solution 1 : | + | Solution of question 1 : |
<center><math> H(s) = 2s+1 </math></center><br/> | <center><math> H(s) = 2s+1 </math></center><br/> | ||
<center><math> G(s) = \frac{10}{s+1} \cdot \frac{1}{s} = \frac{10}{s(s+1)} </math></center><br/> | <center><math> G(s) = \frac{10}{s+1} \cdot \frac{1}{s} = \frac{10}{s(s+1)} </math></center><br/> | ||
<center><math> \frac{X(s)}{U(s)} = \frac{G(s)}{1+G(s)H(s)} = \frac{\frac{10}{s(s+1)}}{1+\frac{10}{s(s+1)} \cdot (2s+1)} = \frac{10}{s(s+1) + 10(2s+1)} </math></center><br/> | <center><math> \frac{X(s)}{U(s)} = \frac{G(s)}{1+G(s)H(s)} = \frac{\frac{10}{s(s+1)}}{1+\frac{10}{s(s+1)} \cdot (2s+1)} = \frac{10}{s(s+1) + 10(2s+1)} </math></center><br/> | ||
| − | <center><math> = \ | + | <center><math> = \frac{10}{s^{2}+s+20s+10} = \frac{10}{s^{2}+21s+10} </math></center><br/> |
---- | ---- | ||
2. (15 pts) For the closed-loop system, shown in Figure 2, find the settling time, using the 2% criterion (in secs). <br/> | 2. (15 pts) For the closed-loop system, shown in Figure 2, find the settling time, using the 2% criterion (in secs). <br/> | ||
<center><math> t_{s} = ? </math></center><br/> | <center><math> t_{s} = ? </math></center><br/> | ||
| + | |||
| + | <center>https://www.projectrhea.org/rhea/dropbox_/40c5d9059656d63a4b7544531047c681/Chang534_f2.png </center> | ||
| + | Solution of question 2: | ||
| + | <center><math> \frac{C(s)}{R(s)}=\frac{16/s^{2}}{1+ \frac{11}{S^{2}} (\frac{1}{4} s + 1)} = \frac{16}{s^{2}+4s+16} </math></center><br/> | ||
| + | <center><math> W_{n}^{2} = 16, \ \ then \ \ W_{n} = 4 </math></center><br/> | ||
| + | <center><math> 2 \xi w_{n} = 8 \xi = 4, \ \ then \xi =\frac{1}{2} </math></center><br/> | ||
| + | <center><math> t_{s} = \frac{4}{\xi W_{n}} =\frac{4}{\frac{1}{2} \cdot 4} = 2 \ s </math></center><br/> | ||
| + | |||
| + | |||
---- | ---- | ||
| Line 38: | Line 47: | ||
<center><math> G(s) = \frac{3}{s(s+1)^{2}} </math></center><br/> | <center><math> G(s) = \frac{3}{s(s+1)^{2}} </math></center><br/> | ||
Find the gain margin, <math> K_{g} </math>, of the closed-loop systems in numbers. <br/> | Find the gain margin, <math> K_{g} </math>, of the closed-loop systems in numbers. <br/> | ||
| − | <center> K_{g} = ? </center><br/> | + | <center><math> K_{g} = ? </math></center><br/> |
| + | |||
| + | Solution of question 3: | ||
| + | <center><math> G(jw) = \frac{3}{s^{3}+2s^{2}+s} |_{s=jw} = \frac{3}{-jw^{3}-2w^{2}+jw} = \frac{3}{-2w^{2} + j(w-w^{3})} </math></center><br/> | ||
| + | <center><math> w - w^{3} = 0</math></center><br/> | ||
| + | Thus, <center><math> w=1</math></center><br/> | ||
| + | <center><math> | G(j1) |=| \frac{3}{-2} | = \frac{3}{2}</math></center><br/> | ||
| + | Thus, <center><math> Kg = \frac{1}{|G(j1)|} = \frac{2}{3}</math></center><br/> | ||
| + | |||
| + | |||
---- | ---- | ||
| Line 44: | Line 62: | ||
<center><math> G_{c}(s) = K_{c}(1+T_{d}s) </math></center><br/> | <center><math> G_{c}(s) = K_{c}(1+T_{d}s) </math></center><br/> | ||
Find <math> T_{d} </math> that achieves this design goals. <br/> | Find <math> T_{d} </math> that achieves this design goals. <br/> | ||
| − | <center> T_{d} = ?</center> <br/> | + | <center><math> T_{d} = ? </math></center> <br/> |
| + | |||
| + | Solution of question4: | ||
| + | <center><math>p_{1} = -1 + j2</math></center><br/> | ||
| + | <center><math>G_{c}(p_{1}) = Kc[1+Td(-1+j2)] </math></center><br/> | ||
| + | <center><math>= Kc[1-Td+j(2Td)]</math></center><br/> | ||
| + | Thus, | ||
| + | <center><math>\frac{2Td}{1-Td} = tan 45^{\circ} = 1 </math></center><br/> | ||
| + | Thus, | ||
| + | <center><math>p_{1} = -1 + j2</math></center><br/> | ||
| + | <center><math>2Td = 1-Td</math></center><br/> | ||
| + | <center><math>Td = \frac{1}{3}</math></center><br/> | ||
---- | ---- | ||
5. (15 pts) We wish the dominant complex conjugate poles of the closed-loop system to be located at <math> -4 \pm j 2 \sqrt{3} </math>. The argument of the open loop-transfer function evaluated at the upper dominant pole is 150 degree. We use a lead compensator in the forward path. The transfer function of the compensator is <br/> | 5. (15 pts) We wish the dominant complex conjugate poles of the closed-loop system to be located at <math> -4 \pm j 2 \sqrt{3} </math>. The argument of the open loop-transfer function evaluated at the upper dominant pole is 150 degree. We use a lead compensator in the forward path. The transfer function of the compensator is <br/> | ||
| − | <center> G_{c}(s) = K_{c} \frac{s-z_{c}}{s-p_{c}} </center> <br/> | + | <center><math> G_{c}(s) = K_{c} \frac{s-z_{c}}{s-p_{c}} </math></center> <br/> |
We set <math> z_{c} = -4 </math>, Find <math> p_{c} </math> <br/> | We set <math> z_{c} = -4 </math>, Find <math> p_{c} </math> <br/> | ||
| − | |||
| + | Solution of question5: | ||
| + | <center><math>S_{1} = -4+j2 \sqrt{3} </math></center><br/> | ||
| + | <center><math> \phi = 180^{\circ} - 180^{\circ} = 30^{\circ} </math></center><br/> | ||
| + | <center><math> Gc(s)=Kc \cdot \frac{s+4}{s-p_{c}} </math></center><br/> | ||
| + | <center><math> Gc(s_{1})=Kc \cdot \frac{-4+j2 \sqrt{3}+4}{-4+j2 \sqrt{3}-p_{c}} = \frac{j2 \sqrt{3}}{-4-p_{c}+j2 \sqrt{3}} </math></center><br/> | ||
| + | <center><math>90^{\circ} - arctan(-\frac{2 \sqrt{3}}{4+p_{c}}) = 30^{\circ} </math></center><br/> | ||
| + | Thus, | ||
| + | <center><math> arctan(\frac{2 \sqrt{3}}{4+p_{c}}) = 30^{\circ}</math></center><br/> | ||
| + | <center><math> arctan(\frac{2 \sqrt{3}}{4+p_{c}}) = 60^{\circ} </math></center><br/> | ||
| + | <center><math> p_{c} = -6 </math></center><br/> | ||
---- | ---- | ||
| Line 60: | Line 98: | ||
<center><math> \beta = ? </math></center><br/> | <center><math> \beta = ? </math></center><br/> | ||
| + | Solution of question 6: | ||
| + | <center><math> Kv \cdot \hat{Kc} \cdot \beta = \hat{Kv} </math></center><br/> | ||
| + | Then, | ||
| + | <center><math> 2.5 \times 2 \times \beta = 40 </math></center><br/> | ||
| + | <center><math> \beta = 8 </math></center><br/> | ||
---- | ---- | ||
7. (15 pts) In Figure 3, Bode diagrams are shown of the uncompensated open-loop system with the gain adjusted for the desired error coefficient. It is required that the phase margin of the compensator closed-loop system, using a lag compensator, be 55 degree. Add 5 deg to compensator for the phase lag of the compensator. Select the corner frequency corresponding to the zero of the compensator one decade below the new gain crossover frequency. Find the location the zero of the lag compensator. <br/> | 7. (15 pts) In Figure 3, Bode diagrams are shown of the uncompensated open-loop system with the gain adjusted for the desired error coefficient. It is required that the phase margin of the compensator closed-loop system, using a lag compensator, be 55 degree. Add 5 deg to compensator for the phase lag of the compensator. Select the corner frequency corresponding to the zero of the compensator one decade below the new gain crossover frequency. Find the location the zero of the lag compensator. <br/> | ||
<center><math> z_{c} = ? </math></center><br/> | <center><math> z_{c} = ? </math></center><br/> | ||
| + | |||
| + | <center>https://www.projectrhea.org/rhea/dropbox_/40c5d9059656d63a4b7544531047c681/Chang534_f3.png </center><br/> | ||
| + | Solution of question 7: | ||
| + | <center><math> (-0.3) </math></center><br/> | ||
| + | <center><math> 55^{\circ} + 5^{\circ} = 60^{\circ} </math></center><br/> | ||
| + | <center><math> 180^{\circ} - 120^{\circ} = 60^{\circ} </math></center><br/> | ||
| + | <center><math> -120^{\circ} -> 3 -> 0.3 </math></center><br/> | ||
| + | Thus, | ||
| + | <center><math> (s + 0.3) </math></center><br/> | ||
| + | |||
| + | |||
Latest revision as of 23:58, 23 February 2019
Automatic Control (AC)
Question 1: Feedback Control Systems
August 2007
1. (10 pts) Find the transfer function $ X(s)/U(s) $ of the block diagram, shown in Figure 1.
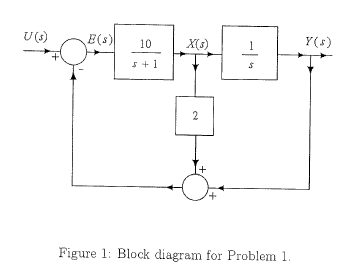
Solution of question 1 :
2. (15 pts) For the closed-loop system, shown in Figure 2, find the settling time, using the 2% criterion (in secs).
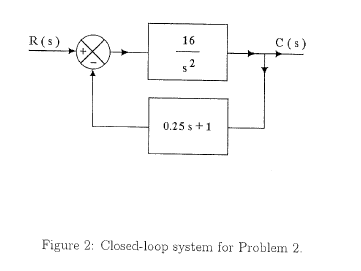
Solution of question 2:
3. (15 pts) A negative unity feedback closed-loop system has the open-loop transfer function
Find the gain margin, $ K_{g} $, of the closed-loop systems in numbers.
Solution of question 3:
Thus,
Thus,
4. (15 pts) We wish the dominant complex conjugate poles of the closed-loop system to be located at $ -1 \pm j2 $. The deficiency angle of the uncompensated closed-loop system at the upper dominant pole is 45 degree. We use a PD compensator in the forward path. The transfer function of the compensator is
Find $ T_{d} $ that achieves this design goals.
Solution of question4:
Thus,
Thus,
5. (15 pts) We wish the dominant complex conjugate poles of the closed-loop system to be located at $ -4 \pm j 2 \sqrt{3} $. The argument of the open loop-transfer function evaluated at the upper dominant pole is 150 degree. We use a lead compensator in the forward path. The transfer function of the compensator is
We set $ z_{c} = -4 $, Find $ p_{c} $
Solution of question5:
Thus,
6. (15 pts) The velocity error coefficient of an uncompensated unity feedback closed-loop system is $ K_{v} =2.5 $. We wish to improve the steady-state performance of the closed-loop system by placing a lag compensator in the forward path. The transfer function of the compensator is
To keep the dominant closed-loop poles in the desired location, we use the gain $ K_{c}=2 $. The desired velocity error coefficient of the compensated closed-loop system is $ K_{v}=40 $. Find $ \beta $ that achieves this design goal.
Solution of question 6:
Then,
7. (15 pts) In Figure 3, Bode diagrams are shown of the uncompensated open-loop system with the gain adjusted for the desired error coefficient. It is required that the phase margin of the compensator closed-loop system, using a lag compensator, be 55 degree. Add 5 deg to compensator for the phase lag of the compensator. Select the corner frequency corresponding to the zero of the compensator one decade below the new gain crossover frequency. Find the location the zero of the lag compensator.
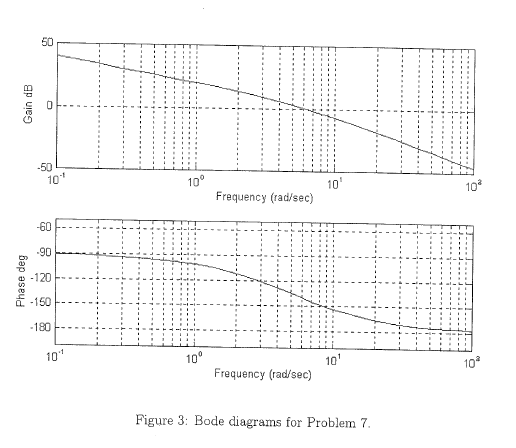
Solution of question 7:
Thus,

