| (14 intermediate revisions by 2 users not shown) | |||
| Line 11: | Line 11: | ||
<center> <math> \frac{a}{b} = \frac{a+b}{a} = \frac{360^o}{\theta} = \frac{1}{\phi} </math> </center> | <center> <math> \frac{a}{b} = \frac{a+b}{a} = \frac{360^o}{\theta} = \frac{1}{\phi} </math> </center> | ||
<center> <math> \theta = \phi \cdot 360^o \approx 137.5^o </math> </center> | <center> <math> \theta = \phi \cdot 360^o \approx 137.5^o </math> </center> | ||
| − | This angle minimizes the amount of overlap between the layers of leaves, maximizing the amount of sunlight the plan can receive. One method of seeing why this is the case is to consider the graph <math> y = \frac{1}{\phi} x </math>, plotted in Figure 3. | + | This angle minimizes the amount of overlap between the layers of leaves, maximizing the amount of sunlight the plan can receive <sup>[http://gofiguremath.org/natures-favorite-math/the-golden-ratio/the-golden-angle/ (12)]</sup>. One method of seeing why this is the case is to consider the graph <math> y = \frac{1}{\phi} x </math>, plotted in Figure 3. |
<center> [[File: Graph.png]] </center> | <center> [[File: Graph.png]] </center> | ||
<center> Figure 3: Plot of <math> y = \frac{1}{\phi} </math> with Pairs of Consecutive Fibonacci Numbers </center> | <center> Figure 3: Plot of <math> y = \frac{1}{\phi} </math> with Pairs of Consecutive Fibonacci Numbers </center> | ||
| + | Since the golden ratio is irrational, it will never intersect any of the points on the grid, which represent integer pairs. In fact, this line will miss the grid points better than a line with any other slope; in some sense it is the “most irrational” number. To understand why, it is useful to consider the definition of an irrational number, and how the golden ratio can be related to this definition. | ||
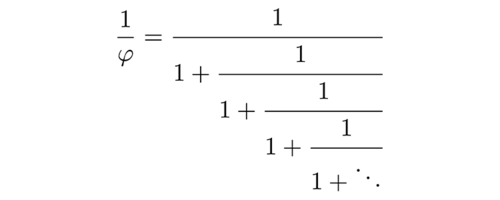
| + | An irrational number is one which cannot be expressed by a fraction. One way of considering the meaning of the "most irrational" number is to find a number that is the hardest to approximate with a fraction. For example, pi, while irrational, is fairly well approximated by <math> \frac{22}{7} </math>. To more closely study the process of approximating irrationals, it is useful to look at continued fractions. The best way to explain a continued fraction is via an example. Consider the continued fraction for <math> \sqrt{2} </math>: | ||
| + | <center> https://www.math.temple.edu/~yury/calendar/img10.png </center> | ||
| + | In a continued fraction, each denominator is given by the sum of an integer and another fraction, continuing infinitely. By cutting off the continued fraction at a given point, the result is a fraction that approximated the given irrational. For example, <math> \sqrt{2} </math> is approximated by: | ||
| + | <center> <math> \sqrt{2} = 1.4142... \approx 1 + \frac{1}{2} = \frac{3}{2} = 1.5 </math> </center> | ||
| + | <center> <math> \sqrt{2} = 1.4142... \approx 1 + \frac{1}{2 + \frac{1}{2}} = \frac{7}{5} = 1.4 </math> </center> | ||
| + | |||
| + | By taking more terms of the continued fraction, the resulting rational number better approximates <math> \sqrt{2} </math>. To see what makes a number have a poor rational approximation, consider the size of the denominator of each fraction. For a large denominator, the fraction is closed to zero, so the cutoff is more accurate. The most irrational number would then be the number whose continued fraction has the largest denominator possible, which is <math> 1 </math>. In fact, the golden ratio is this number <sup>[http://curiosamathematica.tumblr.com/post/114294953296/golden-ratio-in-phyllotaxis (14)]</sup> (Note that <math> \phi = 1 + \frac{1}{\phi} </math>: | ||
| + | <center> https://66.media.tumblr.com/b785e47663d0bf7b010698b5dc9069a9/tumblr_inline_pbiu0tUpnc1s0x50x_500.png </center> | ||
| + | |||
| + | Since fractions so poorly approximate the golden ratio, progressing by multiples of the golden ratio is the best choice to avoid nearing integers. For example, if plant leaves used pi instead of the golden ratio, the <math>7^{th}</math> and <math>7 \cdot 22 = 154^{th}</math> leaves would closely overlap since their ratio is close to pi. Since the number of plant leaves must be an integer, arranging them using the golden ratio minimizes their overlap. This concept is discussed in more depth in [https://www.youtube.com/watch?v=sj8Sg8qnjOg "The Golden Ratio (why it is so irrational)"] on the YouTube channel Numberphile. | ||
| + | |||
| + | Often the leaves themselves can be related to the Fibonacci sequence. For example, the veins of some leaves are roughly spaced by the golden ratio. The leaves of the Ginko Tree also have been found to grow with dimensions that include the golden ratio <sup>[http://ginkgopages.blogspot.com/2005/12/ginkgo-golden-number.html (11)]</sup>. Examples of these phenomena are shown in Figures 4 and 5. | ||
| + | |||
| + | <center> https://i.pinimg.com/originals/b7/fd/af/b7fdaf12eb4839e7be7afb9b7c75d8be.png </center> | ||
| + | <center> Figure 4: Organization of Venation of a Leaf </center> | ||
| + | <center> http://photos1.blogger.com/blogger/1708/1872/320/ginkgo_golden_number3.jpg </center> | ||
| + | <center> Figure 5: The Ginko Tree's Leaf and the Fibonacci Ratio </center> | ||
| + | |||
| + | |||
| + | |||
| + | [[Walther MA279 Fall2018 topic1|Back to Home]] | ||
<br><br>[[Category:MA279Fall2018Walther]] | <br><br>[[Category:MA279Fall2018Walther]] | ||
Latest revision as of 23:44, 2 December 2018
The Fibonacci Sequence in Leaves
The Fibonacci sequence is present in both the structure and arrangement of leaves in many plants. Since plants rely on photosynthesis, they want to maximize the amount of sunlight that strikes their leaves. The vertical growth of many plants means that leaves can cover up each other. To minimize this effect, the leaves are grown such that the angle between each successive leaf is the golden angle, as shown in Figure 2.

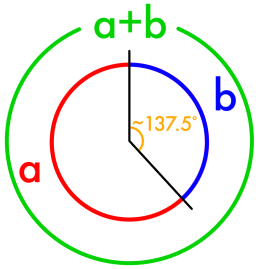
The golden angle is simply the golden ratio applied to a circle: it is the smaller angle formed by two arcs that are related by the golden ratio.
This angle minimizes the amount of overlap between the layers of leaves, maximizing the amount of sunlight the plan can receive (12). One method of seeing why this is the case is to consider the graph $ y = \frac{1}{\phi} x $, plotted in Figure 3.
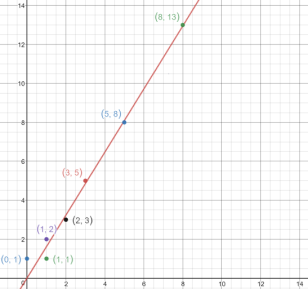
Since the golden ratio is irrational, it will never intersect any of the points on the grid, which represent integer pairs. In fact, this line will miss the grid points better than a line with any other slope; in some sense it is the “most irrational” number. To understand why, it is useful to consider the definition of an irrational number, and how the golden ratio can be related to this definition.
An irrational number is one which cannot be expressed by a fraction. One way of considering the meaning of the "most irrational" number is to find a number that is the hardest to approximate with a fraction. For example, pi, while irrational, is fairly well approximated by $ \frac{22}{7} $. To more closely study the process of approximating irrationals, it is useful to look at continued fractions. The best way to explain a continued fraction is via an example. Consider the continued fraction for $ \sqrt{2} $:

In a continued fraction, each denominator is given by the sum of an integer and another fraction, continuing infinitely. By cutting off the continued fraction at a given point, the result is a fraction that approximated the given irrational. For example, $ \sqrt{2} $ is approximated by:
By taking more terms of the continued fraction, the resulting rational number better approximates $ \sqrt{2} $. To see what makes a number have a poor rational approximation, consider the size of the denominator of each fraction. For a large denominator, the fraction is closed to zero, so the cutoff is more accurate. The most irrational number would then be the number whose continued fraction has the largest denominator possible, which is $ 1 $. In fact, the golden ratio is this number (14) (Note that $ \phi = 1 + \frac{1}{\phi} $:
Since fractions so poorly approximate the golden ratio, progressing by multiples of the golden ratio is the best choice to avoid nearing integers. For example, if plant leaves used pi instead of the golden ratio, the $ 7^{th} $ and $ 7 \cdot 22 = 154^{th} $ leaves would closely overlap since their ratio is close to pi. Since the number of plant leaves must be an integer, arranging them using the golden ratio minimizes their overlap. This concept is discussed in more depth in "The Golden Ratio (why it is so irrational)" on the YouTube channel Numberphile.
Often the leaves themselves can be related to the Fibonacci sequence. For example, the veins of some leaves are roughly spaced by the golden ratio. The leaves of the Ginko Tree also have been found to grow with dimensions that include the golden ratio (11). Examples of these phenomena are shown in Figures 4 and 5.



