(→Periodic Functions) |
(→Non-periodic Functions) |
||
| Line 20: | Line 20: | ||
Here is what the function looks like when graphed: | Here is what the function looks like when graphed: | ||
| + | |||
| + | [[Image:np_exp_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 09:39, 5 September 2008
Periodic Functions
A Continuous Time signal is said to be periodic if there exists $ T > 0 $ such that $ x(t+T)=x(t) $
A Discrete Time signal is said to be periodic if there exists $ N > 0 $ (where N is an integer) such that $ x[n+N]=x[n] $
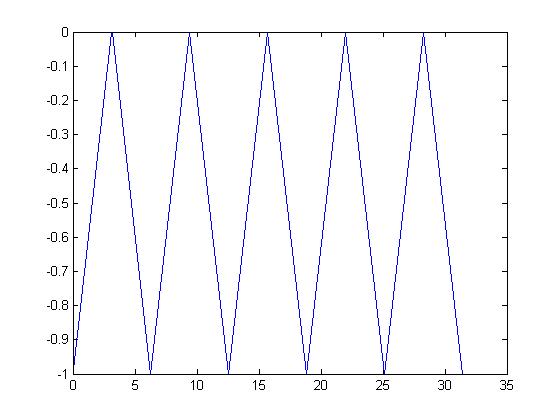
An example of a CT periodic signal is $ x(t) = sawtooth(t) $:
As you can see the function has a fundamental period of two Pi. Therefore any multiple of two Pi is a period.
Non-periodic Functions
A Continuous Time signal is said to be non-periodic if there is no value of $ T > 0 $ that satisfies $ x(t+T)=x(t) $
A Discrete Time signal is said to be non-periodic if there is no value of $ N > 0 $ (where N is an integer) that satisfies$ x[n+N]=x[n] $
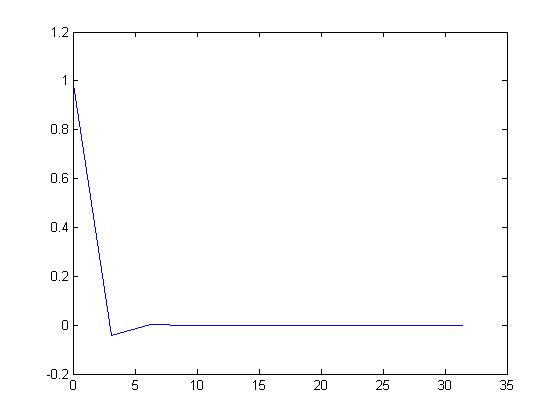
An example of a non-periodic continuous time signal would be $ \ x(t) = e^{(-1 + j)t} $. This goes to show that not all complex exponential functions are periodic.
Here is what the function looks like when graphed: