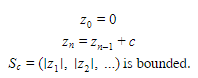| Line 26: | Line 26: | ||
Fractals can also be generated from abstract mathematical constructs. Two famous examples of these are the Mandelbrot and the Cantor set, which are both briefly explored below: | Fractals can also be generated from abstract mathematical constructs. Two famous examples of these are the Mandelbrot and the Cantor set, which are both briefly explored below: | ||
| − | [[File:Pff2:PNG]] | + | [[File:Pff2.PNG]] |
| + | |||
| + | The Mandelbrot Set is the set of all complex numbers c such that the recursively defined sequence S<sub>c</sub>: | ||
| + | |||
| + | [[File:Pfe1.PNG]] | ||
| + | |||
| + | In Figure 2, the Mandelbrot set is visually depicted on the complex plane in black, while the other colors depict values of c for with S<sub>c</sub> diverges from a predetermined neighborhood n in k iterations, i.e. z<sub>k</sub> > n. The visual format of the Mandelbrot Set sparked interest amongst many mathematicians, and hence was formally defined as a fractal. | ||
| + | |||
| + | The Cantor Comb, generated by the Cantor Set, is another famous example of a fractal generated from abstract mathematics. Surprisingly, a similar variant of this fractal is observed in various forms of music, one of which we will analyze and discover in greater detail. The Cantor comb can be generated as shown: | ||
Revision as of 20:07, 2 December 2018
PDF Version: File:Proj.pdf
MA 279, Fall 2018: Fractals and Music
Daksh Jotwani, Daniel Atallah, Noah Talbot, Zoe Phillips
Introduction
“If music is invented to mimic a certain harmony in nature, the mountains are sounds; rivers are lyrics” - Zhi-Yuan Su and Tzuyin Wu
We have always been fascinated by the infinite number of patterns surrounding our environment. Patterns are a huge part of our daily observations; from uniformly distributed branches on a tree, to clouds colliding to form familiar objects, we seek to find structure in everything we see, hear, and feel around us.
A subset of patterns that we observe has been classified as fractals. Fractals are generally depicted visually, since we primarily rely on vision to observe our surroundings. These patterns, however, are also observed in a multitude of natural phenomena, and we seek to explore aural examples of them.
Music is a sequence of temporally structured sounds which are sonically appealing to the human ear. Since music is sequential, aural, and possesses a well-defined structure, we believe that exploring the structural patterns of music could lead to observation of some interesting fractals and applications of them. Therefore, we have chosen to explore and document some fascinating fractals which have been observed in the field of music.
Background
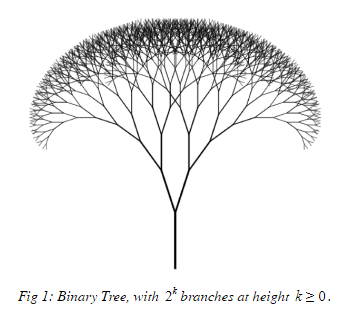
Fractals are infinite self-similar patterns. These patterns are generated by non-terminating sequences, and are usually defined recursively. Fractals are well-observed in nature, and hence are very familiar, as shown by the example below:
The tree above is self-similar, since a new tree can be formed by snapping a branch off the tree. The tree can also be infinitely generated using the following procedure: each branch must split into two new branches. This procedure is also recursive, and is defined concretely as a binary tree in many applications of modern mathematics and computer science.
Fractals can also be generated from abstract mathematical constructs. Two famous examples of these are the Mandelbrot and the Cantor set, which are both briefly explored below:
The Mandelbrot Set is the set of all complex numbers c such that the recursively defined sequence Sc:
In Figure 2, the Mandelbrot set is visually depicted on the complex plane in black, while the other colors depict values of c for with Sc diverges from a predetermined neighborhood n in k iterations, i.e. zk > n. The visual format of the Mandelbrot Set sparked interest amongst many mathematicians, and hence was formally defined as a fractal.
The Cantor Comb, generated by the Cantor Set, is another famous example of a fractal generated from abstract mathematics. Surprisingly, a similar variant of this fractal is observed in various forms of music, one of which we will analyze and discover in greater detail. The Cantor comb can be generated as shown: