| Line 17: | Line 17: | ||
What is most shocking, though, is that Penrose tilings were deliberately constructed; they are man-made. Quasicrystals, however, exist in nature, and yet one may wonder how the atypical symmetries were formed by a force other than man. In 2014, Penrose himself theorized that quasicrystals may be the result of quantum forces acting upon the structure, though this is unfounded as of yet. Penrose tilings, of course, will start from a central point or shape and move outwards, dictated by the hand of man but limited by the golden ratio. How, then, do quasicrystals keep a “memory,” so to speak, of the shapes and structures that “work” to create a lattice like that observed by Schechtman? This question has yet to be answered satisfactorily. | What is most shocking, though, is that Penrose tilings were deliberately constructed; they are man-made. Quasicrystals, however, exist in nature, and yet one may wonder how the atypical symmetries were formed by a force other than man. In 2014, Penrose himself theorized that quasicrystals may be the result of quantum forces acting upon the structure, though this is unfounded as of yet. Penrose tilings, of course, will start from a central point or shape and move outwards, dictated by the hand of man but limited by the golden ratio. How, then, do quasicrystals keep a “memory,” so to speak, of the shapes and structures that “work” to create a lattice like that observed by Schechtman? This question has yet to be answered satisfactorily. | ||
| + | |||
| + | References/further reading: | ||
| + | https://www.pbs.org/newshour/science/quasicrystals-win-chemistry-nobel Marder, Jenny. “What Are Quasicrystals, and What Makes Them Nobel-Worthy?” PBS, Public Broadcasting Service, 5 Oct. 2011, www.pbs.org/newshour/science/quasicrystals-win-chemistry-nobel. | ||
| + | |||
| + | https://www.britannica.com/science/crystal Mahan, Gerald D. “Crystal.” Encyclopædia Britannica, Encyclopædia Britannica, Inc., 12 Oct. 2017, www.britannica.com/science/crystal. | ||
| + | |||
| + | http://www.xtal.iqfr.csic.es/Cristalografia/parte_03_1_1-en.html Ripoll, Martin Martinez. Crystallography. The Symmetry of Crystals, www.xtal.iqfr.csic.es/Cristalografia/parte_03_1_1-en.html. | ||
| + | |||
| + | https://motherboard.vice.com/en_us/article/4x3me3/quasicrystals-are-natures-impossible-matter Oberhaus, Daniel. “Quasicrystals Are Nature's Impossible Matter.” Motherboard, VICE, 3 May 2015, motherboard.vice.com/en_us/article/4x3me3/quasicrystals-are-natures-impossible-matter. | ||
| + | |||
| + | https://physics.aps.org/story/v28/st14 Monroe, Don. “Focus: Nobel Prize–Discovery of Quasicrystals.” Physics, American Physical Society, 7 Oct. 2011, physics.aps.org/story/v28/st14. | ||
[[Category:MA279Fall2018Walther]] | [[Category:MA279Fall2018Walther]] | ||
Revision as of 16:34, 2 December 2018
While Penrose tilings certainly prove interesting within the realm of mathematical abstraction itself, now that we have related methods to develop them and their connection to the golden ratio, let us now discuss a notable analogue in the realm of the physical. In physics and chemistry, a crystal has historically been postulated as any solid with its structure, i.e. of atoms and molecules, displaying a “long-range order;” that is, it retains a repeating latticed structure or motif. These can be contrasted with amorphous solids, which have no such repeating structures or motifs.
 https://www.acs.org/content/acs/en/education/resources/highschool/chemmatters/past-issues/archive-2014-2015/candymaking.html
https://www.acs.org/content/acs/en/education/resources/highschool/chemmatters/past-issues/archive-2014-2015/candymaking.html
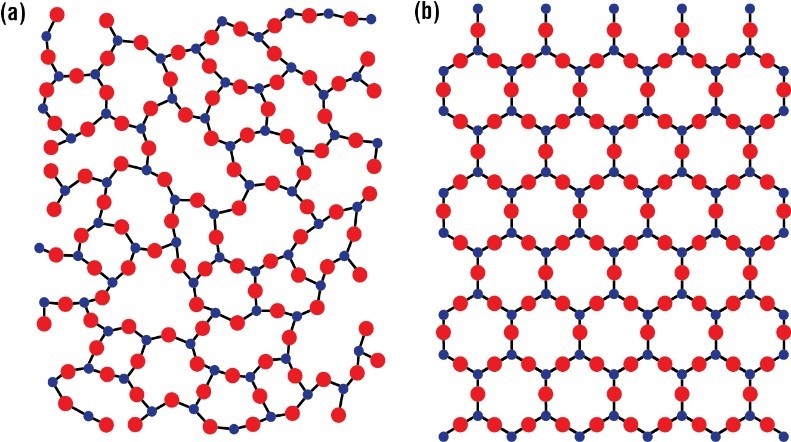
The above image clearly displays a crystalline pattern on the right, while the lattice on the left is clearly amorphous. While both of these displayed lattices are two-dimensional, they will realistically extend into three; they could, for instance, exist in a cubic form. To picture this, one only has to imagine the patterns seen above to extend into or out of this page. It is apparently clear that the repeating motifs historically required of a crystalline solid readily lend themselves to translational and rotational symmetry of different flavors. Crystals as defined in this way quite clearly have translational symmetry; they are intrinsically periodic. One can move the lattice in any direction and it will quite easily fit back into the originating pattern. The rotational symmetries of classically-defined crystals; however, have been considered quite restrictive. Much like tilings, since crystals are periodic by this definition, they can only have three-, four-, or six-fold symmetry, as mentioned previously in this work. In fact, from an intuitive standpoint, one can almost consider crystals as defined in this way as “layers” of tilings. Because of this, properties of tilings very readily carry over to crystals.
Defining crystals in this hard and fast way was regarded as dogma until April 8, 1982, when Israeli professor Dan Schechtman made a Nobel-Prize-winning discovery that startled both him and the scientific world, drawing an interesting parallel to the concept of Penrose tilings. Studying a rapidly-cooled aluminum and manganese alloy, through diffraction, Schechtman found a structure that, notably, had five-fold rotational symmetry but no translational symmetry. The “gaps” one would usually find in such a structure were filled by what scientists today call “glue atoms,” arranged in novel shapes.
Schechtman had discovered what are today called “quasicrystals,” crystals that have no periodic structure or repeating motif but nonetheless have a sense of order due to their unusual rotational symmetries. He was so taken aback by his discovery and its paradigm-shifting potential that he was reported to have said to himself “there can be no such creature” upon looking at the diffraction pattern. He waited two years to publish his work for fear of backlash from the scientific community.
It is apparent that quasicrystals have several connections to Penrose tilings. Certainly, for one, there are conceptual and historical framework parallels. Both Penrose and Schechtman made discoveries that allowed for unconventional rotational symmetries and types of order; Penrose’s tilings did this for the two-dimensional plane, while Schechtman did this for the three-dimensional plane with quasicrystals. In a way, quasicrystals represent the three-dimensional extension of Penrose tilings. This especially seems obvious considering that Penrose first and foremost proved that tilings could have five-fold rotational symmetry, albeit only in tilings that are aperiodic, while Schechtman proved the exact same thing for crystals. One can quite easily conceptualize the quasicrystal under the framework of Penrose tilings; both account for a sense of order but a lack of periodicity.
What is most shocking, though, is that Penrose tilings were deliberately constructed; they are man-made. Quasicrystals, however, exist in nature, and yet one may wonder how the atypical symmetries were formed by a force other than man. In 2014, Penrose himself theorized that quasicrystals may be the result of quantum forces acting upon the structure, though this is unfounded as of yet. Penrose tilings, of course, will start from a central point or shape and move outwards, dictated by the hand of man but limited by the golden ratio. How, then, do quasicrystals keep a “memory,” so to speak, of the shapes and structures that “work” to create a lattice like that observed by Schechtman? This question has yet to be answered satisfactorily.
References/further reading: https://www.pbs.org/newshour/science/quasicrystals-win-chemistry-nobel Marder, Jenny. “What Are Quasicrystals, and What Makes Them Nobel-Worthy?” PBS, Public Broadcasting Service, 5 Oct. 2011, www.pbs.org/newshour/science/quasicrystals-win-chemistry-nobel.
https://www.britannica.com/science/crystal Mahan, Gerald D. “Crystal.” Encyclopædia Britannica, Encyclopædia Britannica, Inc., 12 Oct. 2017, www.britannica.com/science/crystal.
http://www.xtal.iqfr.csic.es/Cristalografia/parte_03_1_1-en.html Ripoll, Martin Martinez. Crystallography. The Symmetry of Crystals, www.xtal.iqfr.csic.es/Cristalografia/parte_03_1_1-en.html.
https://motherboard.vice.com/en_us/article/4x3me3/quasicrystals-are-natures-impossible-matter Oberhaus, Daniel. “Quasicrystals Are Nature's Impossible Matter.” Motherboard, VICE, 3 May 2015, motherboard.vice.com/en_us/article/4x3me3/quasicrystals-are-natures-impossible-matter.
https://physics.aps.org/story/v28/st14 Monroe, Don. “Focus: Nobel Prize–Discovery of Quasicrystals.” Physics, American Physical Society, 7 Oct. 2011, physics.aps.org/story/v28/st14.


