| Line 3: | Line 3: | ||
=Approximating Periodic Signals with Finite Fourier Series= | =Approximating Periodic Signals with Finite Fourier Series= | ||
| − | + | In this project, a matlab function will be used to show how a finite number of Fourier Series coefficients can approximate a periodic signal. | |
| + | |||
| + | <gallery> | ||
| + | File:code.png|Caption1 | ||
| + | File:Example.jpg|Caption2 | ||
| + | </gallery> | ||
| + | |||
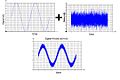
| + | When there are only 1 non-zero term, the time and frequency domain are shown below: | ||
| + | |||
| + | |||
| + | When 2 non-zero terms | ||
| + | |||
| + | |||
| + | When 5 non-zeros terms | ||
| + | |||
| + | |||
| + | When there are 25 non-zero terms | ||
| + | |||
| + | |||
| + | Conclusion: From the above diagrams we are able to distinguish that: As the number of Fourier Series Coefficients increases, the output of approximated periodic signal is more accurate. | ||
| + | |||
| + | |||
| + | |||
| + | A circuit is built to measure the Fourier series of a Square wave | ||
| + | |||
| + | For example, we set s(t) to be square wave with A = 3V, T0 = 0.5*10^-6s | ||
| + | The frequency domain of output shown in spectrum analyzer will be: | ||
| + | |||
| + | The time domain of output shown in oscilloscope will be: | ||
| + | |||
| + | |||
Revision as of 15:15, 21 April 2018
Approximating Periodic Signals with Finite Fourier Series
In this project, a matlab function will be used to show how a finite number of Fourier Series coefficients can approximate a periodic signal.
When there are only 1 non-zero term, the time and frequency domain are shown below:
When 2 non-zero terms
When 5 non-zeros terms
When there are 25 non-zero terms
Conclusion: From the above diagrams we are able to distinguish that: As the number of Fourier Series Coefficients increases, the output of approximated periodic signal is more accurate.
A circuit is built to measure the Fourier series of a Square wave
For example, we set s(t) to be square wave with A = 3V, T0 = 0.5*10^-6s The frequency domain of output shown in spectrum analyzer will be:
The time domain of output shown in oscilloscope will be: