(Created page for ECE QE ES-1, Question 1, part b) |
m (Disambiguate terms by having problems within questions) |
||
| Line 13: | Line 13: | ||
---- | ---- | ||
---- | ---- | ||
| − | == | + | ==Problem 1, part b== |
A developed diagram approach is used, "unrolling" the machine such that increasing <math>\phi</math> (counterclockwise as drawn) is to the left. | A developed diagram approach is used, "unrolling" the machine such that increasing <math>\phi</math> (counterclockwise as drawn) is to the left. | ||
Revision as of 12:48, 16 January 2018
Answers and Discussions for
Problem 1, part b
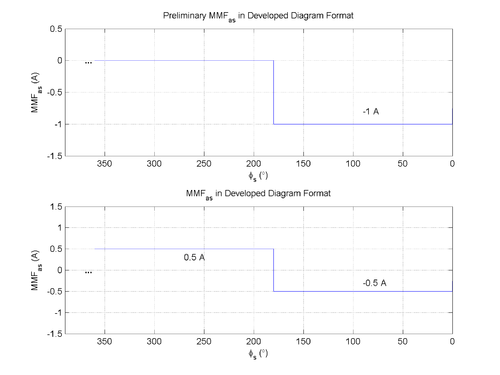
A developed diagram approach is used, "unrolling" the machine such that increasing $ \phi $ (counterclockwise as drawn) is to the left.
Magnetomotive force (MMF) for a machine with concentrated windings may be found as $ \mathbb{F} = \int_{\phi = 0}^{360^\circ} N(\phi) i \, d\phi $.
It is given that $ N_{as} = \mp 1 $ at an inferred position of $ \phi_s = 0^\circ $ and $ \phi_s = 180^\circ $. The current is $ i_{as} = 1 \, \textrm{A} $.
Because $ \oiint_S \vec{B} \cdot d\vec{S} = 0 $, including on the interior surface of the stator and ends of the machine, the average value in the developed diagram of $ B(\phi_s) $ must be 0. The average value of MMF must also be 0 because the airgap is constant, meaning that $ \mathbb{F}(\phi_s) $ and $ B(\phi_s) $ are proportional to each other in the airgap from $ B(\phi_s) = \frac{\mu_0 \mathbb{F}(\phi_s)}{g} $. Thus, the offset of -1.0 A is removed.