(Created page with "=3-D Visualization of Z-Transform= == '''1. Objective''' == This is the page that help students to visualize the Z-Transform in 3-D domain. The relationship between Z tran...") |
|||
| Line 1: | Line 1: | ||
=3-D Visualization of Z-Transform= | =3-D Visualization of Z-Transform= | ||
| − | |||
Revision as of 20:44, 30 November 2017
Contents
3-D Visualization of Z-Transform
1. Objective
This is the page that help students to visualize the Z-Transform in 3-D domain. The relationship between Z transform and Fourier Transform will also be illustrated in 3-D form.
2. Draw the Z Transform plot in 3D format
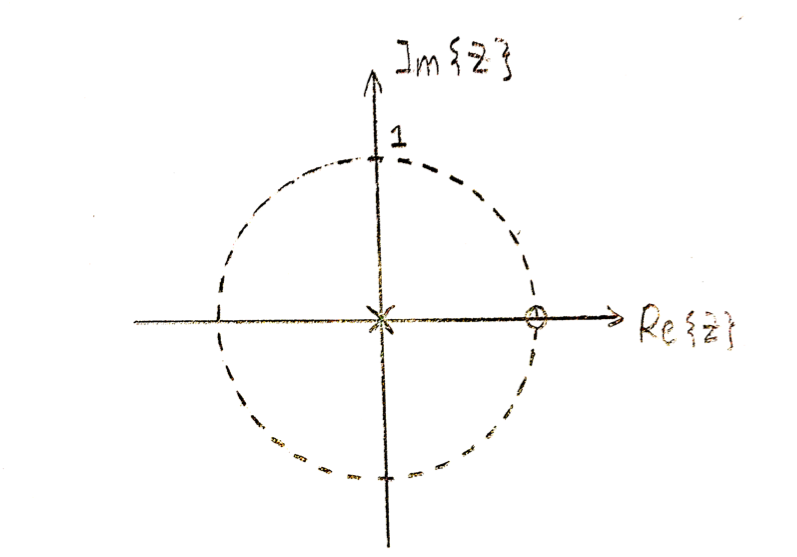
Conventionally, when we draw the 2-D Z transform plot, we assign x-axis as the Real axis and y-axis as the Complex axis. Values on the complex plane will be assigned as numbers or "x"s(when we encounter a pole). Like the figure below:
Figure1: 2D Z-Transform representation
However, if we made this plot in 3D, the entire transfer function will be clearer and more straightforward. Any point that has no value(zeros) will obtain a height of zero and all poles will expand to infinity.
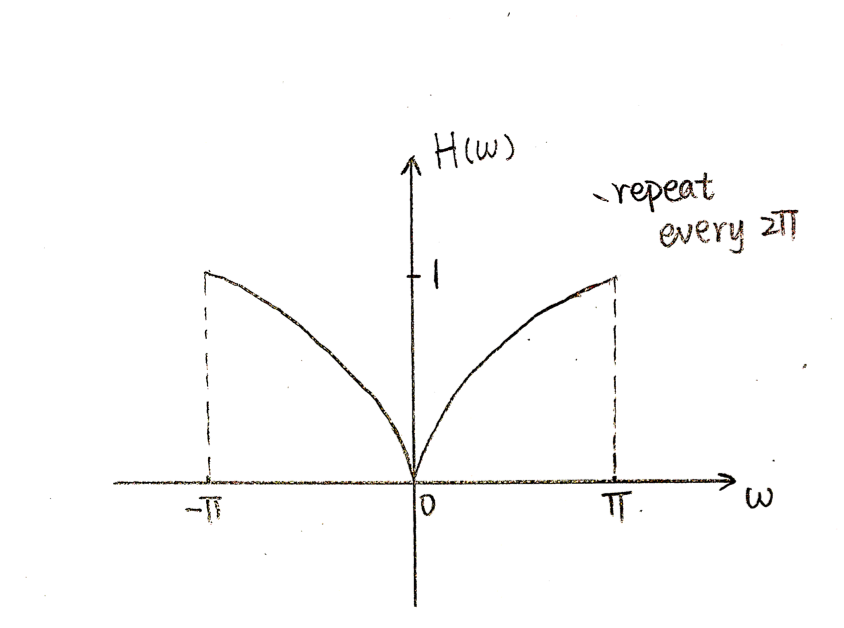
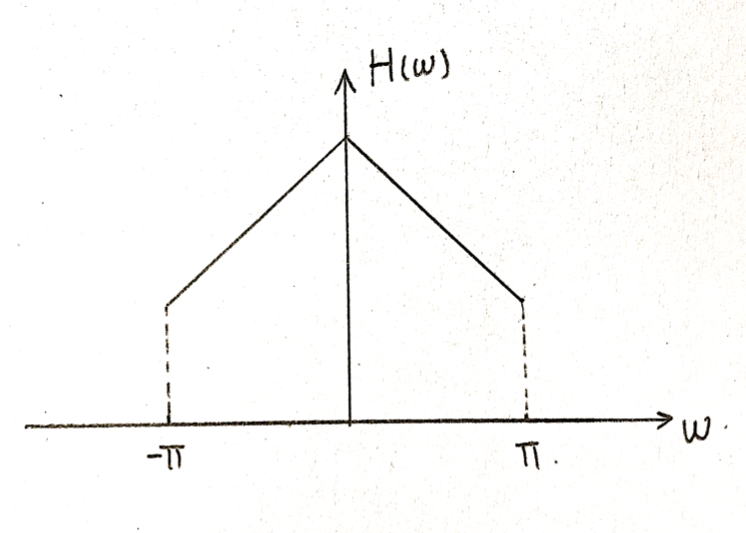
Take the high pass filter y[n] = 1/2*(x[n]-x[n-1]) as an example.
Figure2: Fourier Transform of a high pass filter
Figure3: 3D Z-Transform representation of the high pass filter
3. Obtain Fourier Transform from the Z Transform plot
Suppose we have a 3D Z-Transform plot like the following:
Figure4: 3D Z-Transform representation of something
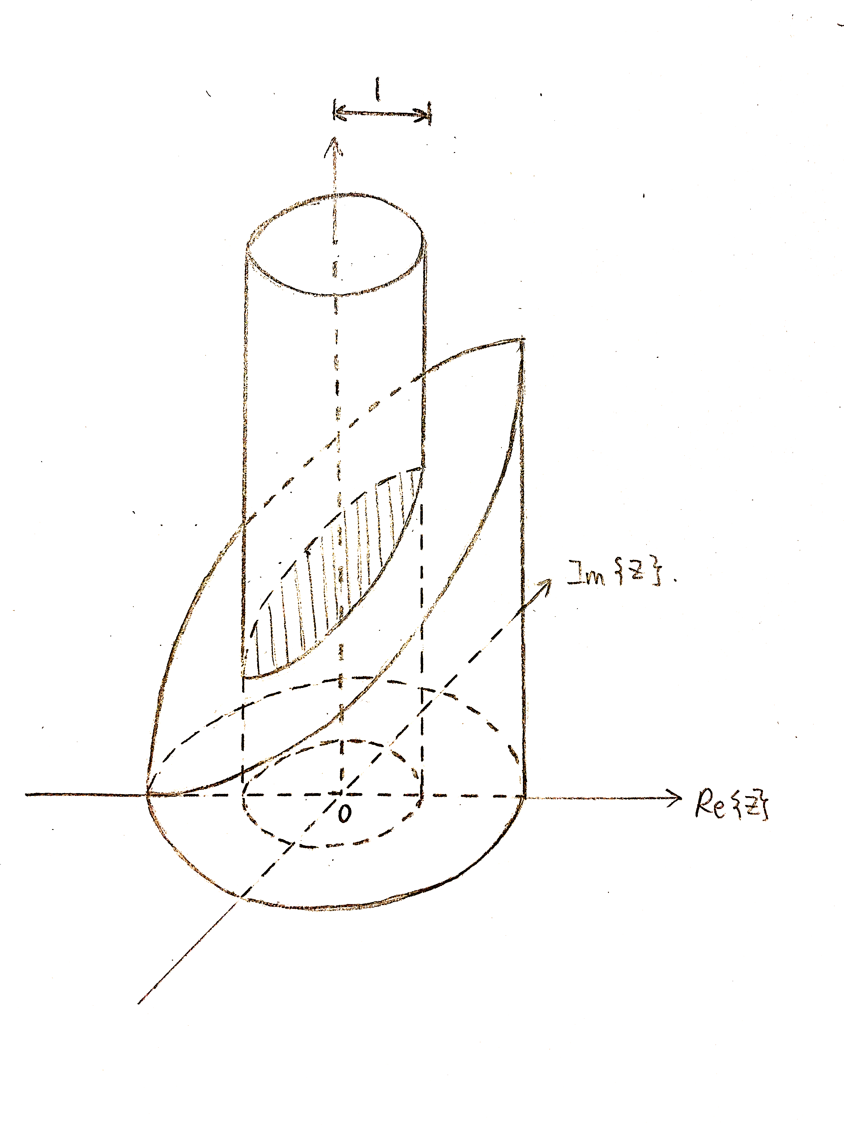
When we want to obtain the Fourier Transform from this plot, we just need to have a cylinder with radius 1, and "cut" the 3D image vertically:
Figure5: 3D graph is cut by a cylinder
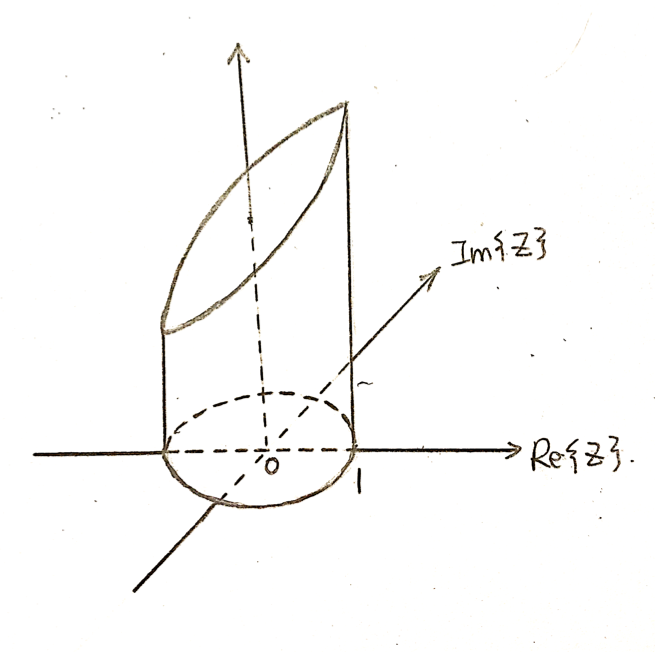
Then, take out the extra part, Leave the cylinder and the edges cut from the Z-Transform:
Figure6: Leave the cut part only
Finally, expand the cylinder onto a plane, now you get the Fourier Transform!
Figure6: Fourier Transform from -pi to pi
Note: This process could also explain why DTFT always have a period of 2pi. When we are drawing graphs outside [-pi, pi], we are actually trace the edge again and again around the circle in Figure6.