(Created page with "Category:ECE Category:QE Category:MN Category:problem solving Category:Dynamics <center> <font size= 4> ECE_PhD_Qualifying_Exams|ECE Ph.D. Qualifying Ex...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 16: | Line 16: | ||
</font size> | </font size> | ||
| − | August | + | August 2012 |
</center> | </center> | ||
---- | ---- | ||
---- | ---- | ||
==Questions== | ==Questions== | ||
| − | All questions are in this [https://engineering.purdue.edu/ECE/Academics/Graduates/ | + | All questions are in this [https://engineering.purdue.edu/ECE/Academics/Graduates/Archived_QE_August_12/MN-2%20QE%2012.pdf link] |
=Solutions of all questions= | =Solutions of all questions= | ||
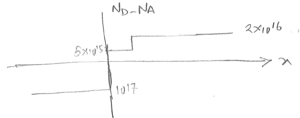
| − | + | a) [[Image:MN2_2012_1.png|Alt text|300x300px]] | |
| − | + | ||
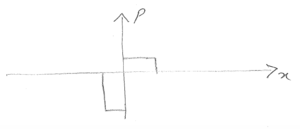
| − | + | b) <math>x_n<1\mu m</math> | |
| − | + | <math>\rho=q(p-n+N_D-N_A)</math> | |
| − | + | [[Image:MN2_2012_2.png|Alt text|300x300px]] | |
| − | + | ||
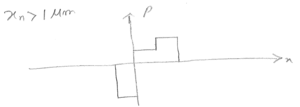
| − | + | <math>x_n>1\mu m</math> | |
| − | + | [[Image:MN2_2012_3.png|Alt text|300x300px]] | |
| + | |||
| + | c) <math> | ||
\begin{align*} | \begin{align*} | ||
| − | + | N_Ax_p&=N_{D1}\cdot1\mu m+N_{D2}(x_n-1)\\ | |
| − | + | x_n&=1.25\mu m\text{ (chk)} | |
| − | & | + | |
| − | + | ||
| − | + | ||
\end{align*} | \end{align*} | ||
</math> | </math> | ||
| − | + | d)<math> | |
| − | + | ||
| − | <math> | + | |
\begin{align*} | \begin{align*} | ||
| − | + | E_{max}&=\frac{qN_Ax_p}{k_s\epsilon_0}\\ | |
| − | + | \text{where;}\\ | |
| − | \ | + | x_p&=\sqrt{\frac{2k_s\epsilon_0}{q}\cdot \frac{N_{D1}}{N_A(N_{D1}+N_A)}\cdot V_{bi}}\\ |
| − | + | \text{and }V_{bi}&=\frac{kT}{q}\ln\frac{N_AN_{D1}}{n_i^2} | |
\end{align*} | \end{align*} | ||
</math> | </math> | ||
| − | + | e)<math> | |
| − | + | \rho=\begin{cases} | |
| − | + | 0 &x<-x_p\\ | |
| − | + | -qN_A &-x_p\le x\le \text{ region 1}\\ | |
| − | \ | + | qN_{D1} & 0\le x\le x_{n1}\text{ region 2}\\ |
| + | qN_{D2} & x_{n1}\le x\le x_{n2}\text{ region 3}\\ | ||
| + | 0 & x>x_{n2} | ||
| + | \end{cases} | ||
</math> | </math> | ||
| + | need to solve; <math>\frac{dE}{dx}=\frac{\rho}{\epsilon}</math> | ||
| − | + | ||
| − | + | ||
| − | \ | + | * region 1 |
| − | + | <math> | |
| − | + | \int_{E(-x_p)}^{E(x)}dE = \frac{-qN_A}{k_s\epsilon_0}\int_{-x_p}^xdx | |
| − | + | </math> | |
| − | + | <math> | |
| − | + | \implies E(x)=\frac{-qN_A}{k_s\epsilon_0}(x+x_p) | |
| − | + | </math> | |
| − | + | at <math>x=0</math> | |
| − | + | <math> | |
| − | + | E(0) = \frac{-qN_A}{k_s\epsilon_0}x_p | |
| − | + | ||
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</math> | </math> | ||
| − | + | * region 2 | |
| − | + | <math> | |
| − | + | \int_{E(0)}^{E(x)}dE = \frac{qN_{D1}}{k_s\epsilon_0}\int_{0}^xdx | |
| − | \ | + | </math> |
| + | <math> | ||
| + | \implies E(x)=\frac{qN_{D1}}{k_s\epsilon_0}x+\frac{qN_A}{k_s\epsilon_0}x_p | ||
</math> | </math> | ||
| − | + | * region 3 | |
| − | + | <math> | |
| − | + | \int_{E(x)}^{E(x_{n2})}dE = \frac{qN_{D2}}{k_s\epsilon_0}\int_{x}^{x_{n2}}dx | |
| + | </math> | ||
| + | <math> | ||
| + | \implies 0-E(x)=\frac{qN_{D2}}{k_s\epsilon_0}(x_{n2}-x) | ||
| + | </math> | ||
| + | <math> | ||
| + | \implies E(x)=\frac{qN_{D2}}{k_s\epsilon_0}(x-x_{n2}) | ||
| + | </math> | ||
| + | ------------------------------------------------------------------------------------ | ||
---- | ---- | ||
[[ECE_PhD_Qualifying_Exams|Back to ECE Qualifying Exams (QE) page]] | [[ECE_PhD_Qualifying_Exams|Back to ECE Qualifying Exams (QE) page]] | ||
Latest revision as of 09:52, 6 August 2017
MICROELECTRONICS and NANOTECHNOLOGY (MN)
Question 2: Junction Devices
August 2012
Questions
All questions are in this link
Solutions of all questions
b) $ x_n<1\mu m $
$ \rho=q(p-n+N_D-N_A) $
$ x_n>1\mu m $
c) $ \begin{align*} N_Ax_p&=N_{D1}\cdot1\mu m+N_{D2}(x_n-1)\\ x_n&=1.25\mu m\text{ (chk)} \end{align*} $
d)$ \begin{align*} E_{max}&=\frac{qN_Ax_p}{k_s\epsilon_0}\\ \text{where;}\\ x_p&=\sqrt{\frac{2k_s\epsilon_0}{q}\cdot \frac{N_{D1}}{N_A(N_{D1}+N_A)}\cdot V_{bi}}\\ \text{and }V_{bi}&=\frac{kT}{q}\ln\frac{N_AN_{D1}}{n_i^2} \end{align*} $
e)$ \rho=\begin{cases} 0 &x<-x_p\\ -qN_A &-x_p\le x\le \text{ region 1}\\ qN_{D1} & 0\le x\le x_{n1}\text{ region 2}\\ qN_{D2} & x_{n1}\le x\le x_{n2}\text{ region 3}\\ 0 & x>x_{n2} \end{cases} $ need to solve; $ \frac{dE}{dx}=\frac{\rho}{\epsilon} $
- region 1
$ \int_{E(-x_p)}^{E(x)}dE = \frac{-qN_A}{k_s\epsilon_0}\int_{-x_p}^xdx $ $ \implies E(x)=\frac{-qN_A}{k_s\epsilon_0}(x+x_p) $ at $ x=0 $ $ E(0) = \frac{-qN_A}{k_s\epsilon_0}x_p $
- region 2
$ \int_{E(0)}^{E(x)}dE = \frac{qN_{D1}}{k_s\epsilon_0}\int_{0}^xdx $ $ \implies E(x)=\frac{qN_{D1}}{k_s\epsilon_0}x+\frac{qN_A}{k_s\epsilon_0}x_p $
- region 3
$ \int_{E(x)}^{E(x_{n2})}dE = \frac{qN_{D2}}{k_s\epsilon_0}\int_{x}^{x_{n2}}dx $ $ \implies 0-E(x)=\frac{qN_{D2}}{k_s\epsilon_0}(x_{n2}-x) $ $ \implies E(x)=\frac{qN_{D2}}{k_s\epsilon_0}(x-x_{n2}) $
------------------------------------------------------------------------------------