(Created page with "3) a) \includegraphics[width=\linewidth]{pec2} <math> \begin{align*} \text{\underline{BC's}:}& &E_{1t}&= E_{2t}\\ & &D_{1n}-D_{2n}&=\rho_s \end{align*} </math> <math> \beg...") |
|||
| Line 3: | Line 3: | ||
a) | a) | ||
| − | + | [[Image:pec2.jpg|Alt text|270x222px]] | |
<math> | <math> | ||
\begin{align*} | \begin{align*} | ||
| − | \text | + | \text{BC's:}& &E_{1t}&= E_{2t}\\ |
& &D_{1n}-D_{2n}&=\rho_s | & &D_{1n}-D_{2n}&=\rho_s | ||
\end{align*} | \end{align*} | ||
| Line 14: | Line 14: | ||
<math> | <math> | ||
\begin{equation*} | \begin{equation*} | ||
| − | \text{In PEC, | + | \text{In PEC, } \bar{E}=0 \longrightarrow \left\{\begin{aligned} E_{1t}&=E_{2t}=0 \\ D_{1n}&=\rho_s \longleftarrow |
| − | \ | + | \text{only normal component left equal \\ to charge on surface of PEC} |
\end{aligned} \right. | \end{aligned} \right. | ||
\end{equation*} | \end{equation*} | ||
| Line 23: | Line 23: | ||
| − | + | [[Image:lnt.jpg|Alt text|270x222px]] | |
<math> | <math> | ||
Latest revision as of 19:05, 18 June 2017
3)
a)
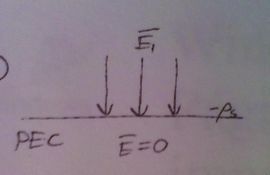
$ \begin{align*} \text{BC's:}& &E_{1t}&= E_{2t}\\ & &D_{1n}-D_{2n}&=\rho_s \end{align*} $
$ \begin{equation*} \text{In PEC, } \bar{E}=0 \longrightarrow \left\{\begin{aligned} E_{1t}&=E_{2t}=0 \\ D_{1n}&=\rho_s \longleftarrow \text{only normal component left equal \\ to charge on surface of PEC} \end{aligned} \right. \end{equation*} $
b)
$ \begin{align*} \bar{E}&=-\nabla V&&\\ &=-\left(\frac{\partial V}{\partial x}\hat{x}+\frac{\partial V}{\partial y}\hat{y}+\frac{\partial V}{\partial z}\hat{z}\right)\\ \end{align*} $
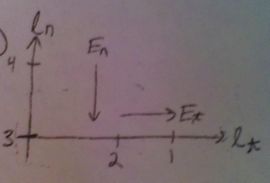
Assume equal potential surface along $ z $ ($ V_{oz} $) then
$ \begin{equation*} \bar{E}=-\left(\frac{\partial V}{\partial x}\hat{x}+\frac{\partial V}{\partial y}\hat{y}\right) \longleftarrow \text{perpendicular to <math>V_{oz}<math>} \end{equation*} $
$ \begin{align*} \text{\underline{Also}:}& &V_1-V_2&=-\int_1^2\bar{E}\cdot d\bar{l}&&\\ & &V_0-V_0&=-\int_1^2\bar{E}_t\cdot d\bar{l}_t=0&&\\ & & &\boxed{E_{t}=0}&&\\ & &V_3-V_4&=-\int_3^4\bar{E}\cdot d\bar{l}&&\\ & &V_0-V_4&=-\int_3^4\bar{E}_n\cdot d\bar{l}_n\neq0&&\\ & & &\boxed{E_{n}\neq0}&& \end{align*} $
$ \therefore $ $ \bar{E} $ must $ \bot $ to equal potential surface.