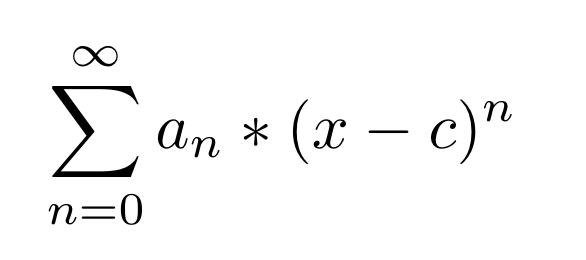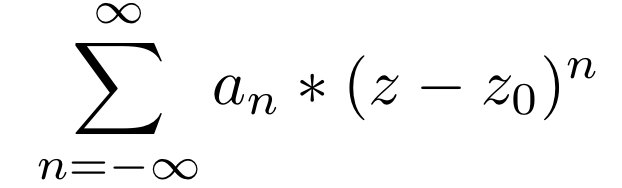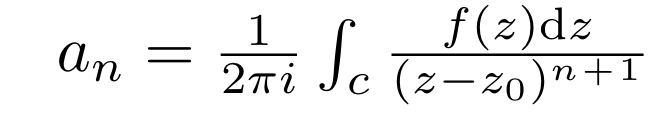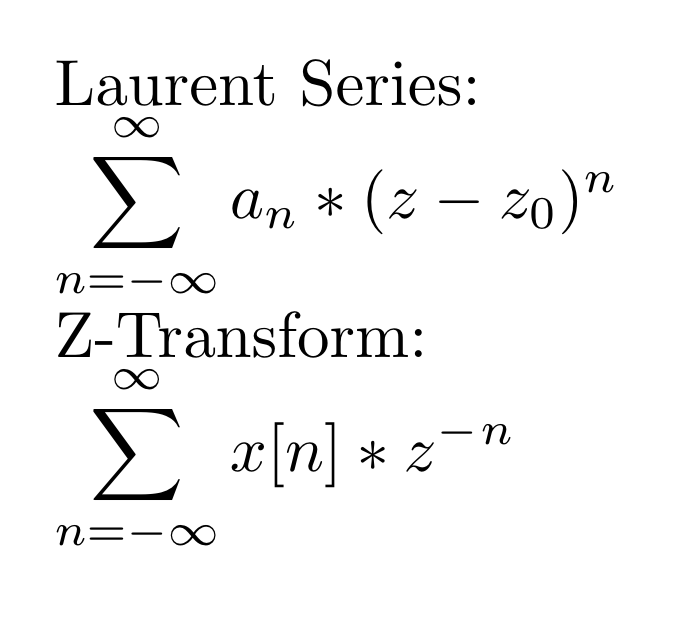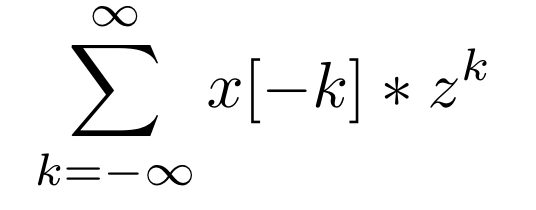| (12 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
'''Introduction:''' | '''Introduction:''' | ||
| − | The Laurent | + | The Laurent Series is a way to describe any analytic function that has its domain on the complex plane. Much like the Taylor Series it is a sum of a variable to a power multiplied by a corresponding coefficient. However, the Laurent Series also has the ability to describe functions with poles by containing negative powers of the complex variable (represented by '''z''') as well. The Laurent Series is the link in DSP between the Discrete Fourier Transform ('''DFT''') and the Z-Transform. |
___________________________________________________________________________________________________________________________________________________ | ___________________________________________________________________________________________________________________________________________________ | ||
| Line 12: | Line 12: | ||
'''Background''' | '''Background''' | ||
| − | There are a few terms that have to be defined to discuss the Laurent | + | There are a few terms that have to be defined to discuss the Laurent Series. A '''smooth''' function on the real numbers has up to a desired number of derivatives that exist, in this case infinitely many. The term '''analytic''' refers to a function on the complex plane that has certain qualities. For the purpose of this explanation analyticness of a function can be treated like the complex equivalent of smoothness. A '''pole''' is a point on a function's domain that is undefined. |
___________________________________________________________________________________________________________________________________________________ | ___________________________________________________________________________________________________________________________________________________ | ||
'''The Taylor Series''' | '''The Taylor Series''' | ||
| − | The Taylor | + | The Taylor Series is a good way to begin discussion of the Laurent Series. The Taylor Series is of the form: |
[[File:Taylor.png|left]] | [[File:Taylor.png|left]] | ||
| Line 27: | Line 27: | ||
where f<sup>(n)</sup> is the n<sup>th</sup> derivative of f(x) | where f<sup>(n)</sup> is the n<sup>th</sup> derivative of f(x) | ||
| − | This series describes any function as a sum of an infinite power series. The area this series accurately describes the function is the '''region of convergence''' of the Taylor Series. This area is limited by where the series returns a finite answer. This region could also be described as the interval (c-r,c+r), where c is the center of the expansion and r is some constant. When describing the Laurent Series r is called the '''radius of convergence''' | + | This series describes any smooth function as a sum of an infinite power series. The area this series accurately describes the function is the '''region of convergence''' of the Taylor Series. This area is limited by where the series returns a finite answer. This region could also be described as the interval (c-r,c+r), where c is the center of the expansion and r is some constant. When describing the Laurent Series r is called the '''radius of convergence'''. |
This sum allows a continuous function to be represented by a sum of a discrete set of values. The concepts of region of convergence and translating a discrete signal into a continuous signal relate directly to the Laurent Series. | This sum allows a continuous function to be represented by a sum of a discrete set of values. The concepts of region of convergence and translating a discrete signal into a continuous signal relate directly to the Laurent Series. | ||
| Line 35: | Line 35: | ||
'''The Laurent Series''' | '''The Laurent Series''' | ||
| − | Using a background in the Taylor Series, the Laurent series can be viewed as the complex extension that allows for the existance of poles and can even give a basic description of those poles. | + | Using a background in the Taylor Series, the Laurent series can be viewed as the complex extension that allows for the existance of poles and can even give a basic description of those poles. The formula is |
| + | [[File:LaurentForm.png|left]] | ||
| + | |||
| + | The Laurent Series seems to be an analogue to the Taylor Series on the complex plane with the sum going to negative infinity instead of stopping at 0. This is a good way to think of the Laurent Series, as it does basically the same thing. The main differences are that the function being described lies on the complex plane and must be analytic instead of smooth. Also, the Laurent Series has a radius of convergence, like the Taylor Series. However, the domain is 2 dimensional, so the radius actually describes a disc in which the series converges to give a valid function. | ||
| + | |||
| + | The coefficients of the Laurent Series can be found with the following formula: | ||
| + | |||
| + | [[File:Lcoeff.png|left]] | ||
| + | |||
| + | One of the interesting things about the Laurent series is that by having negative powered terms to the series, you can assign a number to poles at a point based on the number of negative terms that exist to measure the kind of singularity the function being described at some point. this can range from having no singularity (a<small>n</small>=0 ∀ n<0) or having an infinite (often called '''essential''') singularity where there are infinitely many terms for n<0. This kind of analysis can help give a better description of poles of non-polynomial functions. | ||
| + | |||
| + | The other interesting fact about the Laurent Series is that, like the Taylor Series, it builds a continuous function out of a discrete signal. This is the main way that the Laurent Series is related to DSP: its ability to transfer between discreet, real values and continuous, complex values. | ||
| + | |||
| + | |||
| + | ___________________________________________________________________________________________________________________________________________________ | ||
'''Applications in DSP''' | '''Applications in DSP''' | ||
| − | As was mentioned above, the Laurent series is actually the link between the DFT and the Z-transform. The Z-Transform is function represented by the Laurent | + | As was mentioned above, the Laurent series is actually the link between the DFT and the Z-transform. The Z-Transform is the function represented by the Laurent Series where if x[n] is the DFT of some signal, the n<sup>th</sup> coefficient of the series is x[-n]. This can more easily be seen by comparing the Laurent Series to the Z-transform formula: |
| + | |||
| + | [[File:LZComp.png|left]] | ||
| + | |||
| + | The x[n] is in the place where a<sub>n</sub> would be in the sum, and the z term is to a negative power as well as being centered at zero (z<sub>0</sub>=0). Flipping the signs by setting k=-n gives | ||
| + | |||
| + | [[File:LaurentZFlipped.png|left]] | ||
| + | |||
| + | From here it is clear to see that the z-transformation is a Laurent Series centered at 0. | ||
| + | |||
| + | Having a good understanding of the Laurent Series can then help with computing more difficult Z-transforms, either forward or backward. The concepts involved in finding a Laurent Series are also directly applicable to finding things like the region of convergence of some signal's Z-Transform. Finally, understanding what the Z-tranform is allows you to use facts that apply to the Laurent Series to do things like use [https://en.wikipedia.org/wiki/Residue_theorem the residue theorem] or [https://en.wikipedia.org/wiki/Cauchy%27s_integral_formula Cauchy's integral formula] to analyze the values of the DFT based on its Z-transform. | ||
| + | |||
| + | ___________________________________________________________________________________________________________________________________________________ | ||
| + | '''Referrences''' | ||
| − | + | [1]E. Saff and A. Snider, Fundementals of Complex Analysis with Applications to Engineering and Science, 3rd ed. Upper Saddle River, New Jersey: Pearson Education International, 2003. | |
Latest revision as of 22:40, 23 April 2017
The Laurent Series in DSP
Erik Jensen
Introduction:
The Laurent Series is a way to describe any analytic function that has its domain on the complex plane. Much like the Taylor Series it is a sum of a variable to a power multiplied by a corresponding coefficient. However, the Laurent Series also has the ability to describe functions with poles by containing negative powers of the complex variable (represented by z) as well. The Laurent Series is the link in DSP between the Discrete Fourier Transform (DFT) and the Z-Transform.
___________________________________________________________________________________________________________________________________________________
Background
There are a few terms that have to be defined to discuss the Laurent Series. A smooth function on the real numbers has up to a desired number of derivatives that exist, in this case infinitely many. The term analytic refers to a function on the complex plane that has certain qualities. For the purpose of this explanation analyticness of a function can be treated like the complex equivalent of smoothness. A pole is a point on a function's domain that is undefined.
___________________________________________________________________________________________________________________________________________________ The Taylor Series
The Taylor Series is a good way to begin discussion of the Laurent Series. The Taylor Series is of the form:
the coefficients for a particular function f(x) centered at c∈R can be found with:
an = f(n)(c)/n!
where f(n) is the nth derivative of f(x)
This series describes any smooth function as a sum of an infinite power series. The area this series accurately describes the function is the region of convergence of the Taylor Series. This area is limited by where the series returns a finite answer. This region could also be described as the interval (c-r,c+r), where c is the center of the expansion and r is some constant. When describing the Laurent Series r is called the radius of convergence.
This sum allows a continuous function to be represented by a sum of a discrete set of values. The concepts of region of convergence and translating a discrete signal into a continuous signal relate directly to the Laurent Series.
___________________________________________________________________________________________________________________________________________________
The Laurent Series
Using a background in the Taylor Series, the Laurent series can be viewed as the complex extension that allows for the existance of poles and can even give a basic description of those poles. The formula is
The Laurent Series seems to be an analogue to the Taylor Series on the complex plane with the sum going to negative infinity instead of stopping at 0. This is a good way to think of the Laurent Series, as it does basically the same thing. The main differences are that the function being described lies on the complex plane and must be analytic instead of smooth. Also, the Laurent Series has a radius of convergence, like the Taylor Series. However, the domain is 2 dimensional, so the radius actually describes a disc in which the series converges to give a valid function.
The coefficients of the Laurent Series can be found with the following formula:
One of the interesting things about the Laurent series is that by having negative powered terms to the series, you can assign a number to poles at a point based on the number of negative terms that exist to measure the kind of singularity the function being described at some point. this can range from having no singularity (an=0 ∀ n<0) or having an infinite (often called essential) singularity where there are infinitely many terms for n<0. This kind of analysis can help give a better description of poles of non-polynomial functions.
The other interesting fact about the Laurent Series is that, like the Taylor Series, it builds a continuous function out of a discrete signal. This is the main way that the Laurent Series is related to DSP: its ability to transfer between discreet, real values and continuous, complex values.
___________________________________________________________________________________________________________________________________________________
Applications in DSP
As was mentioned above, the Laurent series is actually the link between the DFT and the Z-transform. The Z-Transform is the function represented by the Laurent Series where if x[n] is the DFT of some signal, the nth coefficient of the series is x[-n]. This can more easily be seen by comparing the Laurent Series to the Z-transform formula:
The x[n] is in the place where an would be in the sum, and the z term is to a negative power as well as being centered at zero (z0=0). Flipping the signs by setting k=-n gives
From here it is clear to see that the z-transformation is a Laurent Series centered at 0.
Having a good understanding of the Laurent Series can then help with computing more difficult Z-transforms, either forward or backward. The concepts involved in finding a Laurent Series are also directly applicable to finding things like the region of convergence of some signal's Z-Transform. Finally, understanding what the Z-tranform is allows you to use facts that apply to the Laurent Series to do things like use the residue theorem or Cauchy's integral formula to analyze the values of the DFT based on its Z-transform.
___________________________________________________________________________________________________________________________________________________
Referrences
[1]E. Saff and A. Snider, Fundementals of Complex Analysis with Applications to Engineering and Science, 3rd ed. Upper Saddle River, New Jersey: Pearson Education International, 2003.