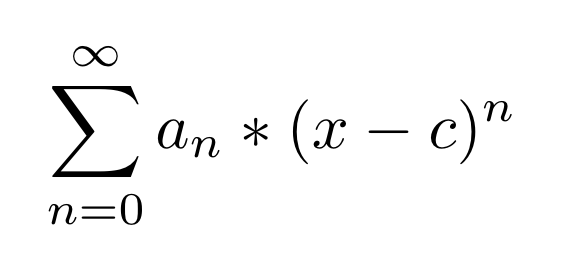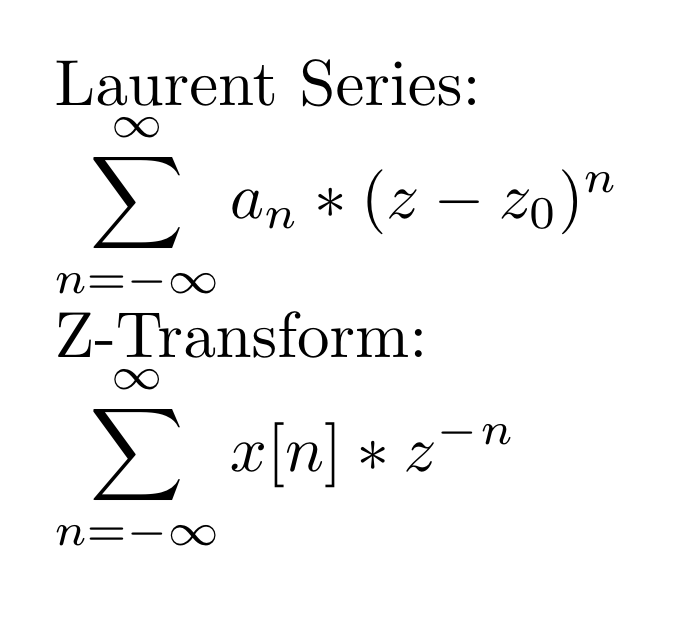| Line 42: | Line 42: | ||
As was mentioned above, the Laurent series is actually the link between the DFT and the Z-transform. The Z-Transform is function represented by the Laurent series where if x[n] is the DFT of some signal, the n<sup>th</sup> coefficient of the series is x[n]. This can more easily be seen by comparing the Laurent series to the Z-transform formula: | As was mentioned above, the Laurent series is actually the link between the DFT and the Z-transform. The Z-Transform is function represented by the Laurent series where if x[n] is the DFT of some signal, the n<sup>th</sup> coefficient of the series is x[n]. This can more easily be seen by comparing the Laurent series to the Z-transform formula: | ||
| − | [[File:LZComp|left]] | + | [[File:LZComp.png|left]] |
The x[n] is in the place where a<sub>n</sub> would be in the sum, and otherwise the formulas are the same. Having a good understanding of the Laurent series can then help with computing more difficult Z-transforms, either forward or backward. The concepts involved in finding a Laurent series are also directly applicable to finding things like the region of convergence of some signal's Z-Transform. Finally, understanding what the Z-tranform is allows you to use facts that apply to the Laurent Series to do things like use the pole-residue theorem or Cauchy's Integral formula to analyze the values of the DFT based on its Z-transform. | The x[n] is in the place where a<sub>n</sub> would be in the sum, and otherwise the formulas are the same. Having a good understanding of the Laurent series can then help with computing more difficult Z-transforms, either forward or backward. The concepts involved in finding a Laurent series are also directly applicable to finding things like the region of convergence of some signal's Z-Transform. Finally, understanding what the Z-tranform is allows you to use facts that apply to the Laurent Series to do things like use the pole-residue theorem or Cauchy's Integral formula to analyze the values of the DFT based on its Z-transform. | ||
Revision as of 21:36, 23 April 2017
The Laurent Series in DSP
Erik Jensen
Introduction:
The Laurent series is a way to describe any analytic function that has its domain on the complex plane. Much like the Taylor Series it is a sum of a variable to a power multiplied by a corresponding coefficient. However, the Laurent series also has the ability to describe functions with poles by containing negative powers of the complex variable (represented by z) as well. The Laurent series is the link in DSP between the Discrete Fourier Transform (DFT) and the Z-Transform.
___________________________________________________________________________________________________________________________________________________
Background
There are a few terms that have to be defined to discuss the Laurent series. The term analytic refers to a function on the complex plane that has certain qualities. For the purpose of this explanation analyticness of a function can be treated like the complex equivalent of infinite differentiability. A pole is a point on a function's domain that is undefined.
___________________________________________________________________________________________________________________________________________________ The Taylor Series
The Taylor series is a good way to begin discussion of the Laurent Series. The Taylor Series is of the form:
the coefficients for a particular function f(x) centered at c∈R can be found with:
an = f(n)(c)/n!
where f(n) is the nth derivative of f(x)
This series describes any function as a sum of an infinite power series. The area this series accurately describes the function is the region of convergence of the Taylor Series. This area is limited by where the series returns a finite answer. This region could also be described as the interval (c-r,c+r), where c is the center of the expansion and r is some constant. When describing the Laurent Series r is called the radius of convergence
This sum allows a continuous function to be represented by a sum of a discrete set of values. The concepts of region of convergence and translating a discrete signal into a continuous signal relate directly to the Laurent Series.
___________________________________________________________________________________________________________________________________________________
The Laurent Series
Using a background in the Taylor Series, the Laurent series can be viewed as the complex extension that allows for the existance of poles and can even give a basic description of those poles.
Applications in DSP
As was mentioned above, the Laurent series is actually the link between the DFT and the Z-transform. The Z-Transform is function represented by the Laurent series where if x[n] is the DFT of some signal, the nth coefficient of the series is x[n]. This can more easily be seen by comparing the Laurent series to the Z-transform formula:
The x[n] is in the place where an would be in the sum, and otherwise the formulas are the same. Having a good understanding of the Laurent series can then help with computing more difficult Z-transforms, either forward or backward. The concepts involved in finding a Laurent series are also directly applicable to finding things like the region of convergence of some signal's Z-Transform. Finally, understanding what the Z-tranform is allows you to use facts that apply to the Laurent Series to do things like use the pole-residue theorem or Cauchy's Integral formula to analyze the values of the DFT based on its Z-transform.