| (8 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
'''1. Introduction''' | '''1. Introduction''' | ||
| − | The early phases of vision handling distinguish highlights in pictures that are important to assessing the structure and properties of items in a scene. Edges are one such component. Edges are huge nearby changes in the picture what's more, are vital components for investigating pictures. Edges commonly happen on the limit between two unique areas in a picture. Edge detection is every now and again the initial phase in recouping data from pictures. Because of its significance, edge detection keeps on being a dynamic research region. | + | The early phases of vision handling distinguish highlights in pictures that are important to assessing the structure and properties of items in a scene. Edges are one such component. Edges are huge nearby changes in the picture what's more, are vital components for investigating pictures. Edges commonly happen on the limit between two unique areas in a picture. Edge detection is every now and again the initial phase in recouping data from pictures. Because of its significance, edge detection keeps on being a dynamic research region. In this project I have illustrated how edge detection works. I have used Gaussian filter to blur the images to remove some for accurate edge line detection. |
'''2. Mathematics behind Edge Detection''' | '''2. Mathematics behind Edge Detection''' | ||
| Line 8: | Line 8: | ||
[[File:Test.jpg|1024px|thumbnail]] | [[File:Test.jpg|1024px|thumbnail]] | ||
| − | [[File:Filter math|1024px|thumbnail]] | + | [[File:Filter math.jpeg|1024px|thumbnail]] |
| Line 21: | Line 21: | ||
When working with images we need to use the two dimensional Gaussian function. This is simply the product of two 1D Gaussian functions (one for each direction) and is given by: | When working with images we need to use the two dimensional Gaussian function. This is simply the product of two 1D Gaussian functions (one for each direction) and is given by: | ||
| − | [[File: | + | [[File:Math2.jpg|600px|thumbnail]] |
| Line 28: | Line 28: | ||
'''3. Edge Detection using Gaussian Filter''' | '''3. Edge Detection using Gaussian Filter''' | ||
| − | [[File:Blockdiagram|thumbnail]] | + | [[File:Blockdiagram.jpeg|1024px|thumbnail]] |
| − | + | ||
| + | Smoothing here refers to use of Gaussian filter to remove noise in images. Matlab has an inbuilt threshold value to detect edges in an image. | ||
| + | |||
'''4. Sample MATLAB Code:''' | '''4. Sample MATLAB Code:''' | ||
%Gaussian filter using MATLAB built_in function | %Gaussian filter using MATLAB built_in function | ||
| + | |||
%Read an Image | %Read an Image | ||
| + | |||
Img = imread('coins.png'); | Img = imread('coins.png'); | ||
| + | |||
A = imnoise(Img,'Gaussian',0.04,0.003); | A = imnoise(Img,'Gaussian',0.04,0.003); | ||
%Image with noise | %Image with noise | ||
| + | |||
figure,imshow(A); | figure,imshow(A); | ||
H = fspecial('Gaussian',[9 9],1.76); | H = fspecial('Gaussian',[9 9],1.76); | ||
| + | |||
GaussF = imfilter(A,H); | GaussF = imfilter(A,H); | ||
| − | figure,imshow(GaussF) | + | |
| + | figure, | ||
| + | |||
| + | imshow(GaussF) | ||
%Sobel Edge Detection after Gaussian Filter | %Sobel Edge Detection after Gaussian Filter | ||
| + | |||
BW1 = edge(GaussF,'sobel'); | BW1 = edge(GaussF,'sobel'); | ||
| + | |||
figure; | figure; | ||
| + | |||
imshow (BW1) | imshow (BW1) | ||
| Line 53: | Line 66: | ||
'''5. References:''' | '''5. References:''' | ||
| − | EEVblog Electronics Community Forum. (n.d.). Retrieved November 26, 2016 | + | EEVblog Electronics Community Forum. (n.d.). Retrieved November 26,2016 from http://www.eevblog.com/forum/microcontrollers/machine-vision(book)/ |
Patrice's Lectures: COMPSCI 373 Semester 1, City Campus. (n.d.). Retrieved November 26, 2016, from https://www.cs.auckland.ac.nz/courses/compsci373s1c/PatricesLectures | Patrice's Lectures: COMPSCI 373 Semester 1, City Campus. (n.d.). Retrieved November 26, 2016, from https://www.cs.auckland.ac.nz/courses/compsci373s1c/PatricesLectures | ||
| Line 60: | Line 73: | ||
Detect Edges in Images. (n.d.). Retrieved November 26, 2016, from https://www.mathworks.com/help/images/edge-detection.html#buh9ylp-13 | Detect Edges in Images. (n.d.). Retrieved November 26, 2016, from https://www.mathworks.com/help/images/edge-detection.html#buh9ylp-13 | ||
| + | |||
| + | Topic: 9 Edge and Line Detection. (n.d.). Retrieved November 26, 2016, from http://www2.ph.ed.ac.uk/~wjh/teaching/dia/documents/edge-ohp.pdf | ||
Latest revision as of 17:53, 30 November 2016
1. Introduction
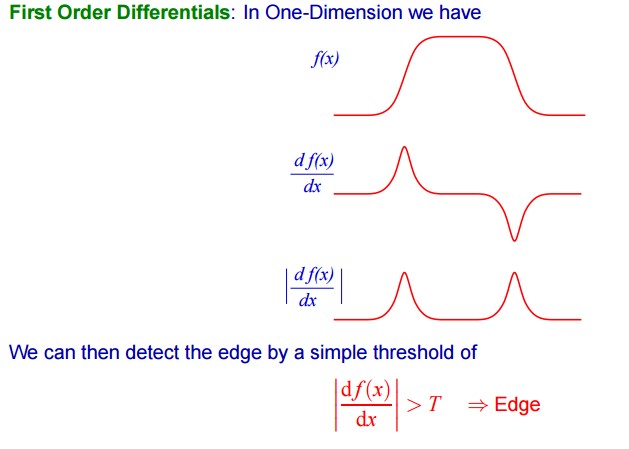
The early phases of vision handling distinguish highlights in pictures that are important to assessing the structure and properties of items in a scene. Edges are one such component. Edges are huge nearby changes in the picture what's more, are vital components for investigating pictures. Edges commonly happen on the limit between two unique areas in a picture. Edge detection is every now and again the initial phase in recouping data from pictures. Because of its significance, edge detection keeps on being a dynamic research region. In this project I have illustrated how edge detection works. I have used Gaussian filter to blur the images to remove some for accurate edge line detection.
2. Mathematics behind Edge Detection
3. Gaussian Filter
Gaussian filtering g is used to blur images and remove noise and detail. In one dimension, the Gaussian function is:
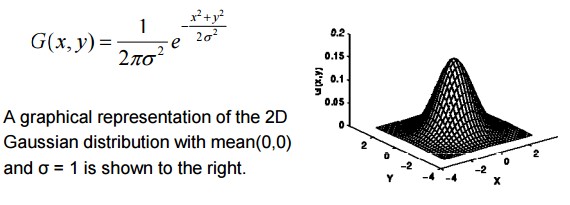
When working with images we need to use the two dimensional Gaussian function. This is simply the product of two 1D Gaussian functions (one for each direction) and is given by:
The Gaussian filter works by utilizing the 2D conveyance as a point-spread capacity. This is accomplished by convolving the 2D Gaussian appropriation work with the picture. We have to deliver a discrete estimate to the Gaussian capacity. This hypothetically requires an endlessly extensive convolution portion, as the Gaussian appropriation is non-zero all over the place. Luckily, the dispersion has moved toward near zero at around three standard deviations from the mean. 99% of the circulation falls inside 3 standard deviations. This implies we can regularly confine the bit size to contain just values 23 This implies we can typically restrict the portion size to contain just values inside three standard deviations of the mean.
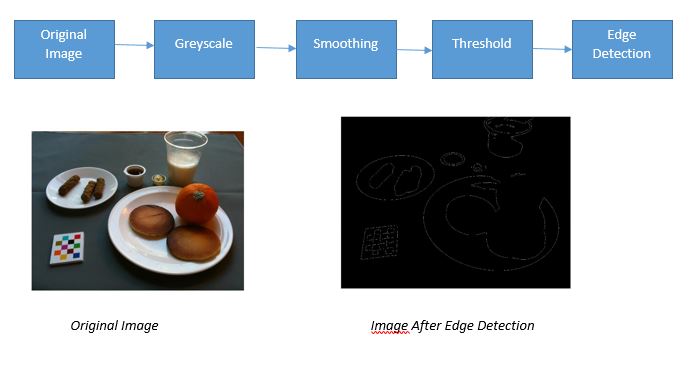
3. Edge Detection using Gaussian Filter
Smoothing here refers to use of Gaussian filter to remove noise in images. Matlab has an inbuilt threshold value to detect edges in an image.
4. Sample MATLAB Code:
%Gaussian filter using MATLAB built_in function
%Read an Image
Img = imread('coins.png');
A = imnoise(Img,'Gaussian',0.04,0.003);
%Image with noise
figure,imshow(A);
H = fspecial('Gaussian',[9 9],1.76);
GaussF = imfilter(A,H);
figure,
imshow(GaussF)
%Sobel Edge Detection after Gaussian Filter
BW1 = edge(GaussF,'sobel');
figure;
imshow (BW1)
5. References:
EEVblog Electronics Community Forum. (n.d.). Retrieved November 26,2016 from http://www.eevblog.com/forum/microcontrollers/machine-vision(book)/
Patrice's Lectures: COMPSCI 373 Semester 1, City Campus. (n.d.). Retrieved November 26, 2016, from https://www.cs.auckland.ac.nz/courses/compsci373s1c/PatricesLectures
Angel, A. (n.d.). Gaussian Filter without using the MATLAB built_in function. Retrieved November 26, 2016, from http://angeljohnsy.blogspot.com/2014/04/gaussian-filter-without-using-matlab.html
Detect Edges in Images. (n.d.). Retrieved November 26, 2016, from https://www.mathworks.com/help/images/edge-detection.html#buh9ylp-13
Topic: 9 Edge and Line Detection. (n.d.). Retrieved November 26, 2016, from http://www2.ph.ed.ac.uk/~wjh/teaching/dia/documents/edge-ohp.pdf