| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==<center>Markov Processes</center>== | ==<center>Markov Processes</center>== | ||
| − | |||
| − | I attempted to model a robot circulating about the origin with small noise in each step. You can directly plug in the Matlab code below. It generated the following images, showing the putative robot spiraling 'inward' or 'outward'. | + | I attempted to model a robot circulating about the origin with small noise in each step. You can directly plug in the Matlab code below. It generated the following images, showing the putative robot spiraling 'inward' or 'outward'. Normally distributed random variables are used to modify the magnitude (M) of the complex vector and rotate the vector in a clockwise direction with a rotation (R) r.v. during each state transition. |
The (first-order, stationary, discrete time, continuous state-space) Markov process representing this simple 'walk' is as follows: | The (first-order, stationary, discrete time, continuous state-space) Markov process representing this simple 'walk' is as follows: | ||
<math> | <math> | ||
| − | X_{t+1} = M X_t e^{-|R|}, where | + | X_{t+1} = \mathrm{M}X_t\mathrm{e}^{-j|\mathrm{R}|},\; \mathrm{where} \;\; \mathrm{M} \sim \mathcal{N}(1,.01),\; \mathrm{R} \sim \mathcal{N}(0, .01) |
</math> | </math> | ||
| Line 17: | Line 16: | ||
| − | Question: | + | Question: Does the noise early in the walk process have a greater effect on the final position of the robot than noise later in the walk process, suggesting a 'butterfly effect'? The second image appears to suggest otherwise, since the robot spirals out early but later spirals inward ending at the red square. |
| − | + | ||
<pre> | <pre> | ||
| Line 31: | Line 29: | ||
% generate next states (probabilistic modifications on current state) | % generate next states (probabilistic modifications on current state) | ||
for j=2:length(walk), | for j=2:length(walk), | ||
| − | walk(j) = walk(j-1)*normrnd(1,std_noise_mag)*( | + | walk(j) = walk(j-1)*normrnd(1,std_noise_mag)*(exp(-i*abs(normrnd(0,std_rot)))); |
end; | end; | ||
plot(walk); grid on; hold on; | plot(walk); grid on; hold on; | ||
Latest revision as of 14:14, 1 May 2016
Markov Processes
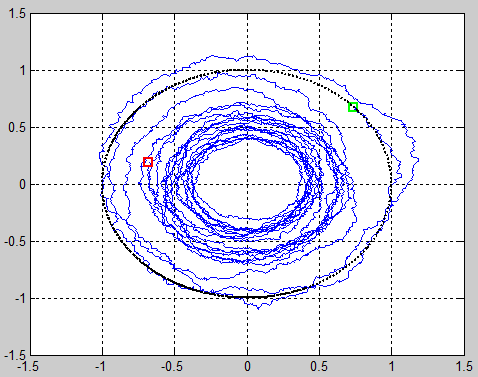
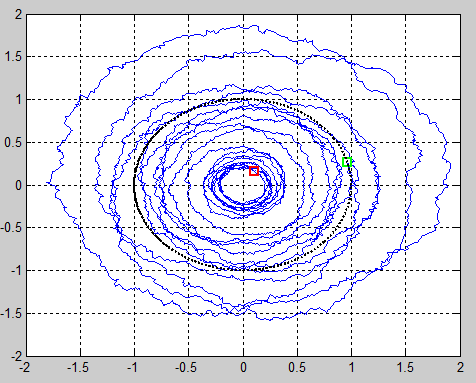
I attempted to model a robot circulating about the origin with small noise in each step. You can directly plug in the Matlab code below. It generated the following images, showing the putative robot spiraling 'inward' or 'outward'. Normally distributed random variables are used to modify the magnitude (M) of the complex vector and rotate the vector in a clockwise direction with a rotation (R) r.v. during each state transition.
The (first-order, stationary, discrete time, continuous state-space) Markov process representing this simple 'walk' is as follows:
$ X_{t+1} = \mathrm{M}X_t\mathrm{e}^{-j|\mathrm{R}|},\; \mathrm{where} \;\; \mathrm{M} \sim \mathcal{N}(1,.01),\; \mathrm{R} \sim \mathcal{N}(0, .01) $
Question: Does the noise early in the walk process have a greater effect on the final position of the robot than noise later in the walk process, suggesting a 'butterfly effect'? The second image appears to suggest otherwise, since the robot spirals out early but later spirals inward ending at the red square.
% set params num_steps = 10000; std_rot = .01; std_noise_mag = .01; % generate random initial state with complex magnitude 1 walk = zeros(1,num_steps); walk(1) = exp(i*rand); % generate next states (probabilistic modifications on current state) for j=2:length(walk), walk(j) = walk(j-1)*normrnd(1,std_noise_mag)*(exp(-i*abs(normrnd(0,std_rot)))); end; plot(walk); grid on; hold on; % plot starting (green) and end (red) markers plot(walk(1), 'gs','LineWidth', 2); plot(walk(length(walk)), 'rs','LineWidth', 2); % generate black circle to compare with "robot" circulation circ = zeros(1,1000); circ(1) = i; for j=2:length(circ), circ(j) = circ(j-1)*i^(2*pi/length(circ)); end; plot(circ,':k','LineWidth', 2); hold off;