| Line 73: | Line 73: | ||
</math> | </math> | ||
| − | Where x is measured in the units of <math>cm</math> and <math> | + | Where x is measured in the units of <math>cm</math> and <math>\mu(x)</math> is measured in units of <math>cm^{-1}</math>. |
a) Calculate the mean of <math> Y_x</math>, i.e. <math>E[Y_x]</math>. | a) Calculate the mean of <math> Y_x</math>, i.e. <math>E[Y_x]</math>. | ||
Revision as of 22:50, 3 December 2015
Communication, Networking, Signal and Image Processing (CS)
Question 5: Image Processing
August 2015
Part 1
Consider the emissive display device which is accurately modeled by the equation
$ \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b&c\\ d&e&f\\ g&h&i \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R\\ G\\ B \end{array}} \right] $
where R, G and B are the red, green, and blue inputs in the range 0 to 255 that are used to modulate physically realizable color primaries.
a) What is the gamma of the device?
b) What are the chromaticity components $ (x_r,y_r), (x_g,y_g) $ and $ (x_b,y_b) $ of the device's three primaries.
c) What are the chromaticity components $ (x_w,y_w) $ of the device's white point.
d) Sketch a chromaticity diagram and plot and label the following on it:
$ \\ 1. (x,y)=(1,0)\\ 2. (x, y) = (0,1)\\ 3. (x, y) = (0,0)\\ 4. (R,G,B) = (255, 0 , 0)\\ 5. (R, G, B) = (0, 255,0)\\ 6. (R,G,B) = (0, 0, 255) $
e) Imagine that the values of $ (R,G,B) $ are quantized to 8 bits, and that you view a smooth gradient from black to white on this device. What artifact are you likely to see, and where in the gradient will you see it?
- Click here to view student answers and discussions
Part 2
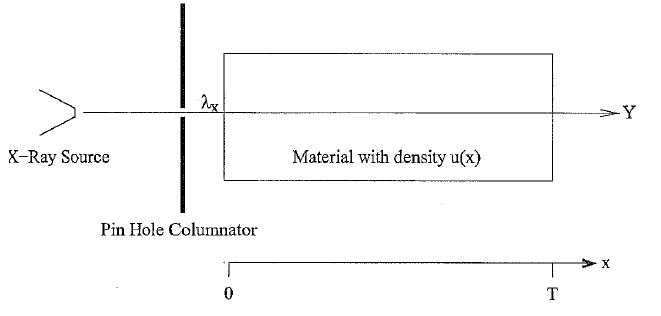
Consider an X-ray imaging system shown in the figure below.
Photons are emitted from an X-ray source and columnated by a pin hole in a lead shield. The columnated X-rays then pass in a straight line through an object of length T with density u(x) where x is the depth into the object. The number of photons in the beam at depth $ x $ is denoted by the random variable $ Y_x $ with Poisson density given by
$ P\{Y_x = k\} = \frac{e^{-\lambda_x}{\lambda}^{k}_{x}}{k!} . $
Where x is measured in the units of $ cm $ and $ \mu(x) $ is measured in units of $ cm^{-1} $.
a) Calculate the mean of $ Y_x $, i.e. $ E[Y_x] $.
b) Calculate the variance of $ Y_x $, i.e. $ E[(Y_x-E[Y_x])^2] $.
c) Write a differential equation which describes the behavior of $ \lambda_x $ as a function of $ x $.
d) Solve the differential equation to form an expression for $ \lambda_x $ in terms of $ \mu(x) $ and $ \lambda_0 $.
e) Calculate an expression for the integral of the density, $ \int_{0}^{T} \mu dx $, in terms of $ \lambda_0 $ and $ \lambda_T $
- Click here to view student answers and discussions