Latest revision as of 22:34, 3 December 2015

ECE Ph.D. Qualifying Exam in Communication Networks Signal and Image processing (CS)

August 2015, Part 1

Part 1 , 2

Solution 1

a) $ \gamma=1 $

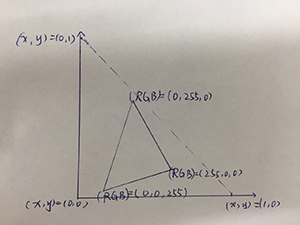
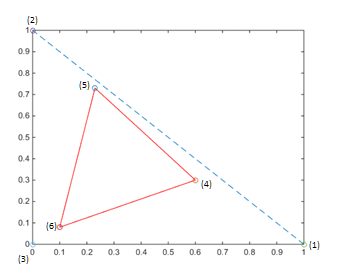
b) $ \left( \begin{array}{c} X_r\\ Y_r \\ Z_r \end{array} \right)＝ \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right)＝ \left( \begin{array}{c} a \\ d \\ g \end{array} \right) $
So $ (x_r,y_r)=(\frac{X_r}{X_r+Y_r+Z_r}, \frac{Y_r}{X_r+Y_r+Z_r})=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
Similarly $ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $, $ (x_b,y_b)＝(\frac{c}{c+f+i},\frac{f}{c+f+i}) $

c) The white point of the device is when the input $ [R, G, B] = [1, 1, 1] $

$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $

d)

e) We are likely to see quantization artifact in dark region.

Solution 2:

a) $ \frac{R}{255}^\alpha=r_{linear}\\ \Rightarrow \gamma=log_{\frac{R}{255}}{(R^{\alpha})}=\frac{ln{(R^{\alpha})}}{ln{\frac{R}{255}}}=\frac{\alpha{ln{R}}}{ln{R}-ln{255}} $

$ \gamma $ should be 1.

b)

$ P_r= \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} a \\ d \\ g \end{array} \right) \\ \Rightarrow x_r=\frac{a}{a+d+g} , y_r=\frac{d}{a+d+g} \\ P_g= \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} b \\ e \\ h \end{array} \right) \\ \Rightarrow x_g=\frac{b}{b+e+h} , y_g=\frac{e}{b+e+h} \\ P_b= \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) \left( \begin{array}{ccc} 0 \\ 0 \\ 1\end{array} \right) = \left( \begin{array}{ccc} c \\ f \\ i \end{array} \right) \\ \Rightarrow x_g=\frac{c}{c+f+i} , y_g=\frac{f}{c+f+i} $

c)

$ W= \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) \left( \begin{array}{ccc} 1 \\ 1 \\ 1\end{array} \right) = \left( \begin{array}{ccc} a+b+c \\ d+e+f \\ g+h+i \end{array} \right) \\ \Rightarrow x_g=\frac{a+b+c}{a+b+c+d+e+f+g+h+i} , y_g=\frac{d+e+f}{a+b+c+d+e+f+g+h+i} $

d)

e) Gamma correction a quantization will create an effect of dynamic range compression for pixels with small values. This will create dark block of shadings in a gradient region instead of a smooth transition.

Back to QE CS question 1, August 2013

Back to ECE QE page: