| Line 30: | Line 30: | ||
We can apply the formula we learned in class to solve for Vout.<br /> | We can apply the formula we learned in class to solve for Vout.<br /> | ||
| − | <math> | + | <math>Vout = (\frac{-R_f}{R_1})Vin</math> |
| − | + | ||
By using the superposition principle we can look at one voltage source at a time, then add them together to find Vout. | By using the superposition principle we can look at one voltage source at a time, then add them together to find Vout. | ||
| + | <math>\begin{align} | ||
Vout = (\frac{-72}{24})4 + (\frac{-72}{36})6\\ | Vout = (\frac{-72}{24})4 + (\frac{-72}{36})6\\ | ||
Vout = -24V | Vout = -24V | ||
Revision as of 17:13, 26 April 2015
Summing Amplifier Practice
Practice question for ECE201: "Linear circuit analysis I"
By: Chinar Dhamija
Topic: Summing Op Amp
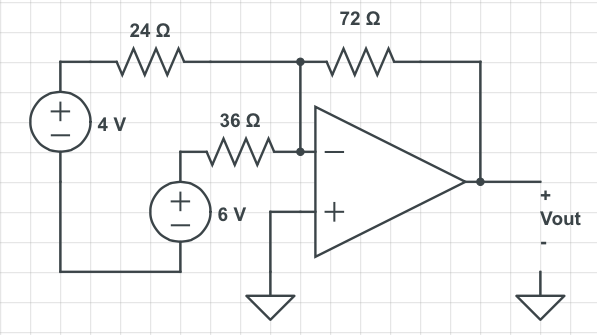
Question
Find the output voltage, Vout.
Answer
First we know that $ V_- $ = $ V_+ $
$ V_- $ = 0V = $ V_+ $
The op amp can be ignored for this particular problem.
We can apply the formula we learned in class to solve for Vout.
$ Vout = (\frac{-R_f}{R_1})Vin $ By using the superposition principle we can look at one voltage source at a time, then add them together to find Vout. $ \begin{align} Vout = (\frac{-72}{24})4 + (\frac{-72}{36})6\\ Vout = -24V \end{align} $
Questions and comments
If you have any questions, comments, etc. please post them below
- Comment 1
- Answer to Comment 1
- Comment 2
- Answer to Comment 2