| (20 intermediate revisions by 2 users not shown) | |||
| Line 21: | Line 21: | ||
#References | #References | ||
---- | ---- | ||
| − | ==Introduction== | + | ==1. Introduction== |
| − | Upsampling is the process of inserting zero-valued samples between the original samples of a signal to increase the sampling rate. | + | Upsampling is the process of inserting zero-valued samples between the original samples of a signal to increase the sampling rate. One way to accomplish upsampling by an integer ratio of 1:D is to interpose D-1 zero samples between each pair of the input samples of the signal. This causes the spectrum of the original signal to repeat at multiples of the original sampling rate. |
| + | |||
| + | The process of upsampling doesn’t change the content of the input signal, and it only introduces the scaling of the time axis by a factor D. Consequently, the operation of upsampling is invertible, which means that it is possible to recover the input signal from samples of the output exactly. | ||
| + | |||
| + | In order to remove or at least attenuate the unwanted image spectra, a low pass filter must be placed immediately after upsampling. In the time domain, the effect is that the zero-valued samples introduced by the upsampler are filled with interpolated values. | ||
---- | ---- | ||
| − | ==Theory== | + | ==2. Theory== |
| + | |||
| + | <center><math> | ||
| + | x_i(n) = | ||
| + | \begin{cases} | ||
| + | x(n/D), & n/D \text{ is an integer} \\ | ||
| + | 0, & \text{otherwise} | ||
| + | \end{cases} | ||
| + | |||
| + | </math></center> | ||
| + | |||
| + | <math></math> | ||
| + | |||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | \ X_i(e^{j\omega}) &= \sum_{n} x(n/D)e^{-j\omega n} \\ | ||
| + | &= \sum_{n} s_D(n)x(n/D)e^{-j\omega n} \\ | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | |||
| + | <math> | ||
| + | \text{Let } m=n/D \Rightarrow n=mD | ||
| + | </math> | ||
| + | |||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | \ X_i(e^{j\omega}) &= \sum_{m} s_D(mD)x(m)e^{-j\omega mD} \\ | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | |||
| + | <math> | ||
| + | \text{But } s_D(mD) \equiv 1 | ||
| + | </math> | ||
| + | |||
| + | <center><math> | ||
| + | \therefore X_i(e^{j\omega}) = X(e^{j\omega D}) | ||
| + | </math></center> | ||
| + | |||
| + | ==Interpolator== | ||
| + | |||
| + | To interpolate between the nonzero saples generated by upsampling, a low pass filter is used. So the combiation of an upsanpler followed by a low pass filter can be referred to as an interpolator. | ||
| + | |||
| + | ---- | ||
| + | ==3. Examples== | ||
| + | Graphical Illustration. Upsampling of X[n] at D = 2. | ||
| + | <center>[[Image:interpolator_1.jpg]]</center> | ||
| + | <center>[[Image:example_1.jpg]]</center> | ||
| + | <center>[[Image:example_2.jpg]]</center> | ||
| + | <center>[[Image:example_3.jpg]]</center> | ||
| + | <center>[[Image:example_4.jpg]]</center> | ||
| + | |||
| + | |||
| + | ==Practical Examples == | ||
| + | |||
| + | There are many applications where the signal of a given sampling rate needs to be converted into an equivalent signal with a different sampling rate. The main reasons could be to increase efficiency or simply to match digital signals that have different rates. | ||
| + | |||
| + | <li>When working with digital images, upsampling is used to enlarge the physical dimensions of an image on a given device. With photoshop we can increase an image dimensions from 2’’ X 2’’ to 3’’ to 3’’ using resampling. Because the image was enlarged, upsampling was required to produce the additional pixels. The number of pixels described in the file, increased from 300 to 450 while the file size increased from 88K to 198K.<br> | ||
| + | <br> | ||
| + | <li>In audio, new samples can be estimated at a higher rate than the input, for example when digital audio sampled at 44.1 kHz is converted to the 48 kHz professional rate used with video.<br> | ||
| + | <br> | ||
| + | <li>In video, upsampling is required in the spatial upconversion from 1280x720 HDTV to 1920X1080 HDTV: 1280 samples in each input line must be converted to 1920 samples in the output, an upsampling ratio 2:3.<br> | ||
| + | <br> | ||
| + | |||
| + | ---- | ||
| + | ==4. Conclusion== | ||
| + | |||
| + | Nowadays we can find a lot of applications where the signal of a given sampling rate needs to be converted into an equivalent signal with a different sampling rate. The main reasons could be to increase efficiency or simply to match digital signals that have different rates. By upsampling a signal | ||
| + | |||
| + | ---- | ||
| + | ==5. References== | ||
| + | |||
| + | [1]. Jan Allebach, Chandrasekar Krithika, "Digital Signal Processing in a Nutshell", Volume I, Second Edition, 2012. | ||
| + | |||
| + | [2]. [https://engineering.purdue.edu/~mboutin/ <span style="color:pink">Mireille Boutin], "ECE438 Digital Signal Processing with Applications," Purdue University, September 24, 2014 | ||
| + | |||
| + | [3]. Mehdi Khosrowpour, "Encyclopedia of Information Science and Technology" Volumes 1-5, 2005. | ||
| + | |||
| + | [4]. Charles A. Poynton, "Digital Video and HDTV: Algorithms and Interfaces", 2003. | ||
| + | |||
| + | [5]. John G. Proakis, Dimitris G. Manolakis, "Digital Signal Processing with Principles, Algorithms, and Applications" 4th Edition,2006 | ||
| + | |||
| + | [6]. Alan V. Oppenheim, Alan S. Willsky, S. Hamid Nawab, "Signals and Systems" 2nd Edition,1996 | ||
| + | |||
| + | [7]. Prof. J. Bilmes, "EE518 Digital Signal Processing, Lecture 9: Upsampling and Downsampling", University of Washington Dept. of Electrical Engineering, October 29, 2001. | ||
| + | |||
| + | |||
| + | ---- | ||
| + | ---- | ||
| + | ---- | ||
| + | ==[[Upsampling_Slecture_Molveraz_review|Questions and Comments]]== | ||
| + | |||
| + | Reviews can be posted on [[Upsampling_Slecture_Molveraz_review|this page]]. | ||
| + | ---- | ||
| + | [[2014_Fall_ECE_438_Boutin_digital_signal_processing_slectures|Back to ECE438 slectures, Fall 2014]] | ||
Latest revision as of 09:01, 14 March 2015
Frequency Domain View of Upsampling
A slecture by exchange student from UNAM, Mexico, Michel Olvera.
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Contents
OUTLINE
- Introduction
- Theory
- Examples
- Conclusion
- References
1. Introduction
Upsampling is the process of inserting zero-valued samples between the original samples of a signal to increase the sampling rate. One way to accomplish upsampling by an integer ratio of 1:D is to interpose D-1 zero samples between each pair of the input samples of the signal. This causes the spectrum of the original signal to repeat at multiples of the original sampling rate.
The process of upsampling doesn’t change the content of the input signal, and it only introduces the scaling of the time axis by a factor D. Consequently, the operation of upsampling is invertible, which means that it is possible to recover the input signal from samples of the output exactly.
In order to remove or at least attenuate the unwanted image spectra, a low pass filter must be placed immediately after upsampling. In the time domain, the effect is that the zero-valued samples introduced by the upsampler are filled with interpolated values.
2. Theory
$ \text{Let } m=n/D \Rightarrow n=mD $
$ \text{But } s_D(mD) \equiv 1 $
Interpolator
To interpolate between the nonzero saples generated by upsampling, a low pass filter is used. So the combiation of an upsanpler followed by a low pass filter can be referred to as an interpolator.
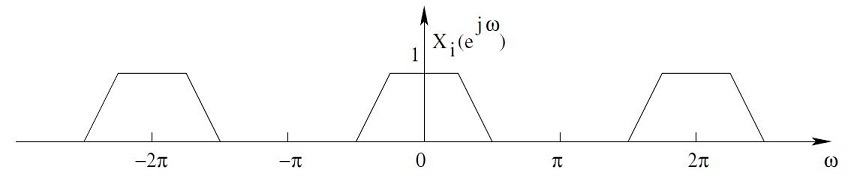
3. Examples
Graphical Illustration. Upsampling of X[n] at D = 2.
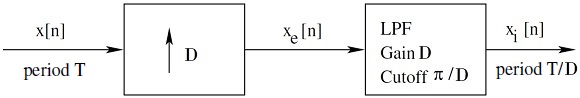
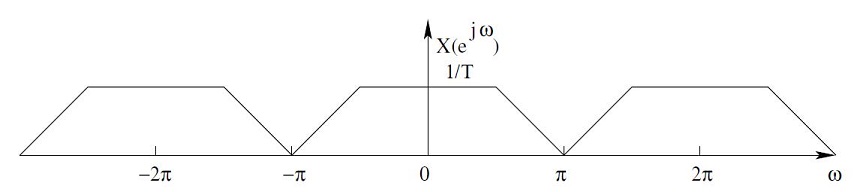
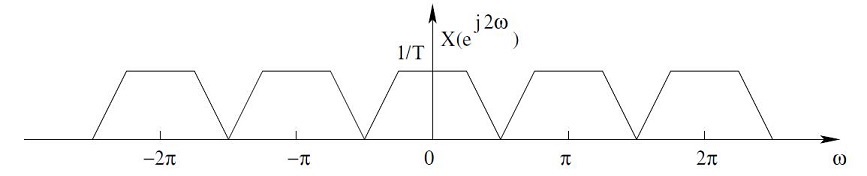
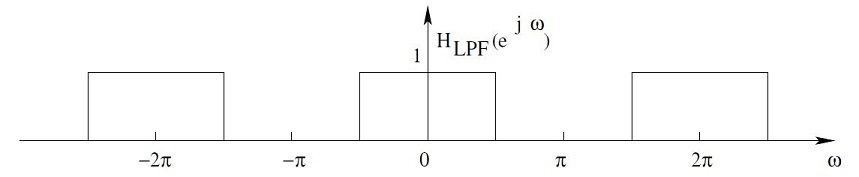
Practical Examples
There are many applications where the signal of a given sampling rate needs to be converted into an equivalent signal with a different sampling rate. The main reasons could be to increase efficiency or simply to match digital signals that have different rates.
4. Conclusion
Nowadays we can find a lot of applications where the signal of a given sampling rate needs to be converted into an equivalent signal with a different sampling rate. The main reasons could be to increase efficiency or simply to match digital signals that have different rates. By upsampling a signal
5. References
[1]. Jan Allebach, Chandrasekar Krithika, "Digital Signal Processing in a Nutshell", Volume I, Second Edition, 2012.
[2]. Mireille Boutin, "ECE438 Digital Signal Processing with Applications," Purdue University, September 24, 2014
[3]. Mehdi Khosrowpour, "Encyclopedia of Information Science and Technology" Volumes 1-5, 2005.
[4]. Charles A. Poynton, "Digital Video and HDTV: Algorithms and Interfaces", 2003.
[5]. John G. Proakis, Dimitris G. Manolakis, "Digital Signal Processing with Principles, Algorithms, and Applications" 4th Edition,2006
[6]. Alan V. Oppenheim, Alan S. Willsky, S. Hamid Nawab, "Signals and Systems" 2nd Edition,1996
[7]. Prof. J. Bilmes, "EE518 Digital Signal Processing, Lecture 9: Upsampling and Downsampling", University of Washington Dept. of Electrical Engineering, October 29, 2001.
Questions and Comments
Reviews can be posted on this page.

