| (17 intermediate revisions by 2 users not shown) | |||
| Line 11: | Line 11: | ||
#Introduction | #Introduction | ||
#Derivation | #Derivation | ||
| − | # | + | #Graphical Example in the Frequency Domain |
#Conclusion | #Conclusion | ||
| + | #Questions/ Comments | ||
</font> | </font> | ||
---- | ---- | ||
| Line 61: | Line 62: | ||
This is just the DTFT of the original signal scaled by D | This is just the DTFT of the original signal scaled by D | ||
| − | + | LPF with filter that has cutoffs at <math>\frac{\pi}{D}</math> and <math>\frac{- \pi}{D}</math> to get <math>Y_2(\omega)</math> | |
| + | |||
| + | Lastly to return to time domain take the Inverse DTFT of <math>Y_2(\omega)</math> to get your up sampled signal <math>y_2[n]</math> | ||
| + | |||
</font> | </font> | ||
| Line 69: | Line 73: | ||
<font size = 3> | <font size = 3> | ||
| + | Note: The gain in this example is 1 | ||
<center>[[Image:fig1_deufel.jpeg]]</center> | <center>[[Image:fig1_deufel.jpeg]]</center> | ||
| − | The first graph shows the signal <math>X_1(w)</math> which is periodic with period 2\pi | + | The first graph shows the signal <math>X_1(w)</math> which is periodic with period <math>2\pi</math> |
| − | The second graph shows the signal <math>X_2(W)</math> which is also periodic with period 2\pi but contains unwanted repetitions of the signal | + | The second graph shows the signal <math>X_2(W)</math> which is also periodic with period <math>2\pi</math> but contains unwanted repetitions of the signal |
The third graph shows the Final Signal after it has been passed through the LPF to remove the unwanted repetitions | The third graph shows the Final Signal after it has been passed through the LPF to remove the unwanted repetitions | ||
| + | |||
| + | In the second graph it is obvious why the signal must pass through a LPF, because the expansion in the time domain resulted in compression in the frequency domain and that has caused the signal to repeat itself with in the range of <math>[-\pi,\pi]</math> and this would cause the reconstruction of the signal to be inaccurate | ||
| + | |||
| + | </font> | ||
---- | ---- | ||
<font size = 4> 4. Conclusion </font> | <font size = 4> 4. Conclusion </font> | ||
| − | Upsampling is an effective way to reduce | + | <font size = 3> |
| − | + | Upsampling is an effective way to reduce time between samples of a signal without resampling the original signal. | |
| − | + | </font> | |
| + | ---- | ||
| + | <font size = 4> | ||
| + | 5. Questions/Comments | ||
| + | </font> | ||
| + | <font size = 3> | ||
| + | You can post questions and comments on this page, Thanks | ||
| + | [[Reviewsdeufel|questions/comments]] | ||
| + | </font> | ||
| + | ---- | ||
| + | <font size = 3>References | ||
| + | - ECE 438 Class notes Prof. Mireille Boutin | ||
| + | </font> | ||
| + | ---- | ||
| + | [[2014_Fall_ECE_438_Boutin_digital_signal_processing_slectures|Back to ECE438 slectures, Fall 2014]] | ||
[[Category:Slecture]] [[Category:ECE438Fall2014Boutin]] [[Category:ECE]] [[Category:ECE438]] [[Category:Frequency_Upsampling]] | [[Category:Slecture]] [[Category:ECE438Fall2014Boutin]] [[Category:ECE]] [[Category:ECE438]] [[Category:Frequency_Upsampling]] | ||
Latest revision as of 09:01, 14 March 2015
Upsampling with an emphasis on the frequency domain
By: Michael Deufel
- Introduction
- Derivation
- Graphical Example in the Frequency Domain
- Conclusion
- Questions/ Comments
1. Introduction
The purpose of Upsampling is to manipulate a signal in order to artificially increase the sampling rate. This is done by...
- Discretize the signal
- Pad original signal with zeros
- Take the DTFT
- Send through a LPF (low pass filter)
- Take the inverse DTFT to return to the time domain
We will overview the whole process but focus on the effect upsampling has in the frequency domain
2. Derivation
We will start with discrete signal $ x_1[n] $
now we "pad with zeros" to define $ x_2[n] $
$ x_2[n] = \begin{cases}x_1[\frac{n}{D}], & \text{if} \frac{n}{D} \in \mathbb{Z} \\0, &\text{else} \end{cases} f $
note: $ D $ must be an integer greater then one
$ x_2[n] $ can also be defined by
$ x_2[n] = \sum_{k} x_1[k] \delta[n-kD] $
Taking the DTFT of $ x_2[n] $
$ X_2(\omega) = \sum_{n} ( \sum_{k} x_1[k] \delta[n-kD]) e^{-j\omega n}) $
switching the order of the summations you can get
$ X_2(\omega)= \sum_{k}x_1[k] ( \sum_{n}\delta[n-kD]) e^{-j\omega n}) $
where,
$ \sum_{n}\delta[n-kD]) e^{-j\omega n} = e^{-j\omega kD} $
therefor,
$ X_2(\omega) = \sum_{k} x_1[k] e^{-j\omega kD} $
This is just the DTFT of the original signal scaled by D
LPF with filter that has cutoffs at $ \frac{\pi}{D} $ and $ \frac{- \pi}{D} $ to get $ Y_2(\omega) $
Lastly to return to time domain take the Inverse DTFT of $ Y_2(\omega) $ to get your up sampled signal $ y_2[n] $
3. Graphical Example in the Frequency Domain
Note: The gain in this example is 1
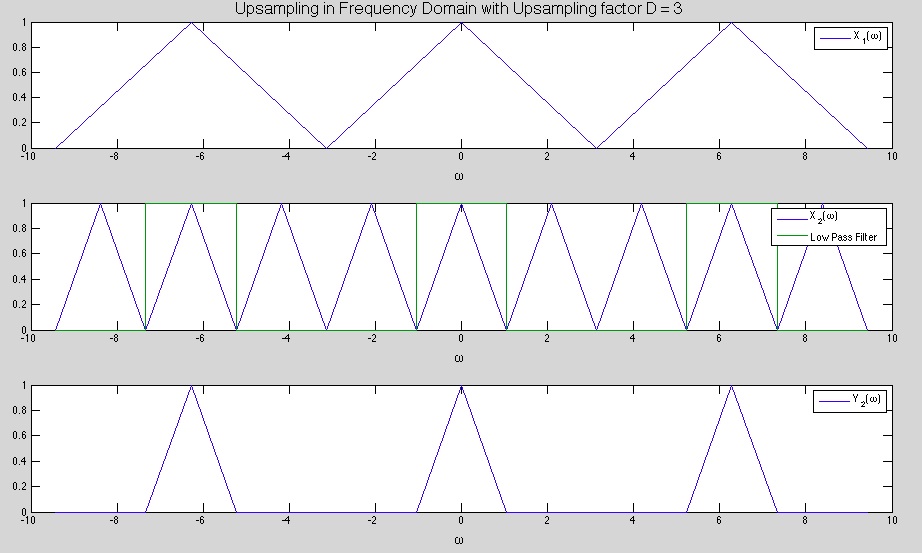
The first graph shows the signal $ X_1(w) $ which is periodic with period $ 2\pi $
The second graph shows the signal $ X_2(W) $ which is also periodic with period $ 2\pi $ but contains unwanted repetitions of the signal
The third graph shows the Final Signal after it has been passed through the LPF to remove the unwanted repetitions
In the second graph it is obvious why the signal must pass through a LPF, because the expansion in the time domain resulted in compression in the frequency domain and that has caused the signal to repeat itself with in the range of $ [-\pi,\pi] $ and this would cause the reconstruction of the signal to be inaccurate
4. Conclusion
Upsampling is an effective way to reduce time between samples of a signal without resampling the original signal.
5. Questions/Comments
You can post questions and comments on this page, Thanks questions/comments
References
- ECE 438 Class notes Prof. Mireille Boutin

