m (add br's) |
|||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 14: | Line 14: | ||
<font size = 3> | <font size = 3> | ||
==Outline== | ==Outline== | ||
| + | #Background | ||
#Introduction | #Introduction | ||
#Derivation | #Derivation | ||
#Example | #Example | ||
#Conclusion | #Conclusion | ||
| + | ---- | ||
---- | ---- | ||
| + | == Background == | ||
| + | <font size = 2> | ||
| + | |||
| + | <math>{f}_{s}</math> = sampling frequency (number of samples/second) Hz | ||
| + | <br> | ||
| + | <math>{T}_{s}</math> = sampling period (number of seconds/sample) seconds | ||
| + | <br> | ||
| + | <math> {f}_{s} = {\frac{1}{{T}_{s}}} </math> | ||
| + | <br><br> | ||
| + | Sampling above Nyquist frequency guarantees a bandlimited sampled CT signal's reconstruction. **add source** | ||
| + | <br> | ||
| + | Define Nyquist Sampling rate as <math> {f}_{Nyquist} = 2{f}_{M} </math> | ||
| + | <br> | ||
| + | <math>{f}_{M} </math> is max frequency of CT signal | ||
| + | <br> | ||
| + | |||
| + | ---- | ||
| + | |||
---- | ---- | ||
| Line 25: | Line 45: | ||
== Introduction == | == Introduction == | ||
| − | + | Sampling at frequencies much larger than Nyquist requires a filter for reconstruction with a less sharp cutoff. A digital LPF can be used to then obtain the reconstructed signal. *add source* | |
<br><br> | <br><br> | ||
Assume <math> {x}_{c}(t) </math> is a bandlimited CT signal, | Assume <math> {x}_{c}(t) </math> is a bandlimited CT signal, | ||
| Line 40: | Line 60: | ||
| + | ---- | ||
| + | ---- | ||
| + | == Derivation == | ||
| + | We want <math> {f}_{u} > {f}_{Nyquist} </math>. In this situation, this means <math> {f}_{u} > {f}_{1} </math>. | ||
| + | <br> | ||
| + | Therefore, we want <math>{T}_{u} < {T}_{1}</math>. (i.e. <math> {x}_{u}[n]</math> is sampled at a higher frequency than <math> {x}_{1}[n]</math>) | ||
| + | <br> In other words, <br> | ||
| + | <math> {T}_{u} = {\frac{{T}_{1}}{D}} </math> for some integer D. | ||
| + | <br> | ||
| + | <br> | ||
| + | <math> {x}_{1}[n] = x_{c}(n{T}_{1})</math> | ||
| + | <br> | ||
| + | <math>{x}_{u}[n] = {x}_{c}(n{T}_{u})</math> | ||
| + | <br> | ||
| + | <math>{x}_{u}[n] ={x}_{1}[n/D] = {x}_{c}(n{T}_{1}({T}_{u}/{T}_{1})) = {x}_{c}(n{T}_{u}) </math>if n/D is an integer | ||
| + | <br> | ||
| + | <math>{x}_{u}[n] = 0 </math> else. | ||
| + | <br><br> | ||
| + | In frequency domain: <br> | ||
| + | <math>{X}_{u}({\omega}) = {\sum_{n = -{\infty}}^{\infty} {x}_{u}[n]e^{-j{\omega}n}}</math> | ||
| + | <br> | ||
| + | <math>{X}_{u}({\omega}) = {\sum_{n = -{\infty}}^{\infty} {x}_{1}[n/D]e^{-j{\omega}n}}</math> | ||
| + | <br> let n=mD <br> | ||
| + | <math>{X}_{u}({\omega}) = {\sum_{m = -{\infty}}^{\infty} {x}_{1}[m]e^{-j{\omega}mD}}</math> | ||
| + | <br> | ||
| + | <math>{X}_{u}({\omega}) ={X}_{1}(D{\omega}) </math> notice this is a rescaled version of <math> {X}_{1} </math> | ||
| + | |||
| + | <br><br> | ||
| + | In order to get <math>{x}_{int}(n) </math>, the reconstructed signal, we need to LPF <math> {X}_{u}({\omega}) </math>. | ||
| + | <br> | ||
| + | <math> {x}_{int}(n) = {x}_{u} * h(n) </math> | ||
| + | <br> | ||
| + | <math> h(n) = sinc(n/D) </math> | ||
---- | ---- | ||
| + | |||
| + | |||
---- | ---- | ||
| − | == | + | == Example == |
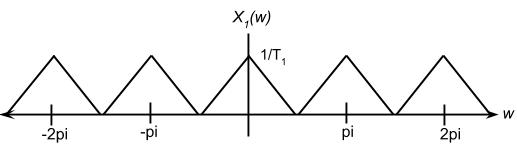
| + | [[Image:X1w.jpg]] | ||
| + | <br> | ||
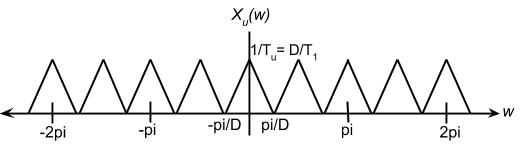
| + | [[Image:Xuw.jpg]] | ||
| + | <br> | ||
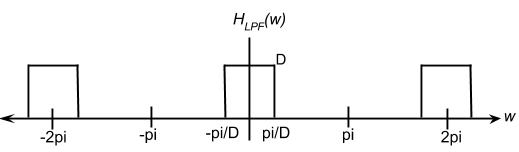
| + | [[Image:Hlpf.jpg]] | ||
| + | <br> | ||
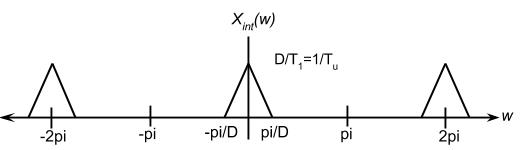
| + | [[Image:Xint.jpg]] | ||
| + | <br> | ||
| + | ---- | ||
| + | |||
| + | ---- | ||
| + | Source: Prof. Mireille Boutin | ||
| + | ---- | ||
| + | ---- | ||
| + | |||
| + | == Questions/Comments == | ||
| + | [[QuestionPage]] | ||
| + | |||
| + | ---- | ||
---- | ---- | ||
| + | [[2014_Fall_ECE_438_Boutin_digital_signal_processing_slectures|Back to ECE438 slectures, Fall 2014]] | ||
Latest revision as of 09:00, 14 March 2015
Frequency Domain View of Upsampling
Why Interpolator needs a LPF after Upsampling
A slecture by ECE student Chloe Kauffman
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Outline
- Background
- Introduction
- Derivation
- Example
- Conclusion
Background
$ {f}_{s} $ = sampling frequency (number of samples/second) Hz
$ {T}_{s} $ = sampling period (number of seconds/sample) seconds
$ {f}_{s} = {\frac{1}{{T}_{s}}} $
Sampling above Nyquist frequency guarantees a bandlimited sampled CT signal's reconstruction. **add source**
Define Nyquist Sampling rate as $ {f}_{Nyquist} = 2{f}_{M} $
$ {f}_{M} $ is max frequency of CT signal
Introduction
Sampling at frequencies much larger than Nyquist requires a filter for reconstruction with a less sharp cutoff. A digital LPF can be used to then obtain the reconstructed signal. *add source*
Assume $ {x}_{c}(t) $ is a bandlimited CT signal,
$ {x}_{1}[n] $ is a DT sampled signal of $ {x}_{c}(t) $ with sampling period $ {T}_{1} $
This leads to the question, can you use
$ {x}_{1}[n] = x_{c}(n{T}_{1}) $
to obtain
$ {x}_{u}[n] = {x}_{c}(n{T}_{u}) $, a signal sampled at a HIGHER sampling frequency than $ {x}_{1}[n] $, without having to fully reconstruct $ {x}_{c}(t) $
Derivation
We want $ {f}_{u} > {f}_{Nyquist} $. In this situation, this means $ {f}_{u} > {f}_{1} $.
Therefore, we want $ {T}_{u} < {T}_{1} $. (i.e. $ {x}_{u}[n] $ is sampled at a higher frequency than $ {x}_{1}[n] $)
In other words,
$ {T}_{u} = {\frac{{T}_{1}}{D}} $ for some integer D.
$ {x}_{1}[n] = x_{c}(n{T}_{1}) $
$ {x}_{u}[n] = {x}_{c}(n{T}_{u}) $
$ {x}_{u}[n] ={x}_{1}[n/D] = {x}_{c}(n{T}_{1}({T}_{u}/{T}_{1})) = {x}_{c}(n{T}_{u}) $if n/D is an integer
$ {x}_{u}[n] = 0 $ else.
In frequency domain:
$ {X}_{u}({\omega}) = {\sum_{n = -{\infty}}^{\infty} {x}_{u}[n]e^{-j{\omega}n}} $
$ {X}_{u}({\omega}) = {\sum_{n = -{\infty}}^{\infty} {x}_{1}[n/D]e^{-j{\omega}n}} $
let n=mD
$ {X}_{u}({\omega}) = {\sum_{m = -{\infty}}^{\infty} {x}_{1}[m]e^{-j{\omega}mD}} $
$ {X}_{u}({\omega}) ={X}_{1}(D{\omega}) $ notice this is a rescaled version of $ {X}_{1} $
In order to get $ {x}_{int}(n) $, the reconstructed signal, we need to LPF $ {X}_{u}({\omega}) $.
$ {x}_{int}(n) = {x}_{u} * h(n) $
$ h(n) = sinc(n/D) $
Example
Source: Prof. Mireille Boutin