| (18 intermediate revisions by the same user not shown) | |||
| Line 21: | Line 21: | ||
a) Write a difference equation that can be used to implement this filter. | a) Write a difference equation that can be used to implement this filter. | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | y[m,n] =& \frac{1}{16}(x[m+1,n-1] + 2x[m,n-1] + x[m-1,n-1] \\ | ||
| + | & + 2x[m+1,n] + 4x[m,n] + 2x[m-1,n] \\ | ||
| + | & + x[m+1,n+1] + 2x[m,n+1] + x[m-1,n+1]) | ||
| + | \end{align}</math> | ||
b) Is this filter separable? Answer yes/no and justify your answer. | b) Is this filter separable? Answer yes/no and justify your answer. | ||
| + | |||
| + | Yes. The coefficient matrix of h[m,n] can be written as product of two vectors. | ||
| + | |||
| + | <math> | ||
| + | \begin{pmatrix} | ||
| + | \frac{1}{16} & \frac{2}{16} & \frac{1}{16} \\ | ||
| + | \frac{2}{16} & \frac{4}{16} & \frac{2}{16} \\ | ||
| + | \frac{1}{16} & \frac{2}{16} & \frac{1}{16} | ||
| + | \end{pmatrix} = | ||
| + | \begin{pmatrix} | ||
| + | \frac{1}{4} \\ | ||
| + | \frac{2}{4} \\ | ||
| + | \frac{1}{4} | ||
| + | \end{pmatrix} \cdot | ||
| + | \begin{pmatrix} | ||
| + | \frac{1}{4} & \frac{2}{4} & \frac{1}{4} | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | Therefore the filter can be decomposed to two 1-D filters. | ||
| + | |||
| + | <math>h_1[m] = \frac{1}{4}(\delta[m+1] + 2\delta[m] +\delta[m-1])</math> | ||
| + | |||
| + | <math>h_2[n] = \frac{1}{4}(\delta[n+1] + 2\delta[n] +\delta[n-1])</math> | ||
| + | |||
c) Compute the DSFT H(u,v) of this filter. Sketch the plot of H(u,0). Sketch the plot of H(0,v). What are the characteristics of this filter (low-pass, band-pass, or high-pass)? | c) Compute the DSFT H(u,v) of this filter. Sketch the plot of H(u,0). Sketch the plot of H(0,v). What are the characteristics of this filter (low-pass, band-pass, or high-pass)? | ||
| + | |||
| + | |||
| + | <math>H_1(\mu) = DTFT\{h_1[m]\} = \frac{1}{4}(e^{j\mu} + 2 + e^{-j\mu}) = \frac{1}{2}(1 + cos\mu)</math> | ||
| + | |||
| + | <math>H_2(\nu) = DTFT\{h_2[n]\} = \frac{1}{4}(e^{j\nu} + 2 + e^{-j\nu}) = \frac{1}{2}(1 + cos\nu)</math> | ||
| + | |||
| + | Using the separability, | ||
| + | |||
| + | <math>H(\mu, \nu) = DSFT\{ h[m,n]\} = H_1(\mu)\cdot H_2(\nu) = \frac{1}{4}(1 + cos\mu)(1 + cos\nu)</math> | ||
| + | |||
| + | <math>H(\mu, 0) = \frac{1}{2}(1 + cos\mu)</math> | ||
| + | |||
| + | [[Image:HW11_prob1_1.jpg]] | ||
| + | |||
| + | So, <math>H(\mu, 0)</math> is a low-pass filter. | ||
| + | |||
| + | |||
| + | <math>H(0, \nu) = \frac{1}{2}(1+cos\nu)</math> | ||
| + | |||
| + | [[Image:HW11_prob1_2.jpg]] | ||
| + | |||
| + | So, <math>H(0, \nu)</math> is a low-pass filter. | ||
| + | |||
d) What is the output image when this filter is applied to the following image (using symmetric boundary conditions)? | d) What is the output image when this filter is applied to the following image (using symmetric boundary conditions)? | ||
| Line 43: | Line 98: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| + | |||
| + | <math>g[m,n]**h[m,n]: \frac{1}{16} X | ||
| + | \begin{array}{cccccccccccc} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
| + | 1 & 3 & 4 & 4 & 4 & 4 & 4 & 4 & 4 & 3 & 1\\ | ||
| + | 3 & 9 &12 &12 &12 &12 &12 &12 &12 & 9 & 3\\ | ||
| + | 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ | ||
| + | 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ | ||
| + | 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ | ||
| + | 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ | ||
| + | 3 & 9 &12 &12 &12 &12 &12 &12 &12 & 9 & 3\\ | ||
| + | 1 & 3 & 4 & 4 & 4 & 4 & 4 & 4 & 4 & 3 & 1\\ | ||
| + | \end{array}</math> | ||
| + | |||
---- | ---- | ||
| Line 81: | Line 152: | ||
<math>\begin{align} | <math>\begin{align} | ||
| − | H(\mu, 0) | + | H(\mu, 0) =& -\frac{1}{9}( e^{j\mu} + e^{-j\nu} \\ |
& + e^{j\mu} + 8 + e^{-j\nu} \\ | & + e^{j\mu} + 8 + e^{-j\nu} \\ | ||
& + e^{j\mu} + e^{-j\nu} ) \\ | & + e^{j\mu} + e^{-j\nu} ) \\ | ||
| Line 88: | Line 159: | ||
<math>\begin{align} | <math>\begin{align} | ||
| − | H(0, \nu) | + | H(0, \nu) =& -\frac{1}{9} (e^{-j\nu} + e^{-j\nu} + e^{-j\nu} \\ |
| − | & | + | & + 8 \\ |
| − | & + e^{j | + | & + e^{j\nu} + e^{j\nu} + e^{j\nu}) \\ |
| + | =& -\frac{1}{9}(8+6cos{\mu}) | ||
\end{align}</math> | \end{align}</math> | ||
| + | |||
| + | <math>|H(\mu, 0)| = \frac{1}{9}(8+6cos{\mu})</math> | ||
| + | |||
| + | [[Image:HW11_prob2_1.jpg]] | ||
| + | |||
| + | So, <math>H(\mu, 0)</math> is a high-pass filter. | ||
| + | |||
| + | |||
| + | <math>|H(0, \nu)| = \frac{1}{9}(8+6cos{\nu})</math> | ||
| + | |||
| + | [[Image:HW11_prob2_2.jpg]] | ||
| + | |||
| + | So, <math>H(0, \nu)</math> is a high-pass filter. | ||
| Line 110: | Line 195: | ||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
\end{array} | \end{array} | ||
| − | </math> | + | </math> |
| + | |||
| + | <math>g[m,n]**h[m,n]: \frac{1}{9} X | ||
| + | \begin{array}{cccccccccccc} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | ||
| + | -1&-2 &-3 &-3 &-3 &-3 &-3 &-3 &-3 &-2 & 1\\ | ||
| + | -2& 5 & 3 & 3 & 3 & 3 & 3 & 3 & 3 & 5 &-2\\ | ||
| + | -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ | ||
| + | -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ | ||
| + | -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ | ||
| + | -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ | ||
| + | -2& 5 & 3 & 3 & 3 & 3 & 3 & 3 & 3 & 5 &-2\\ | ||
| + | -1&-2 &-3 &-3 &-3 &-3 &-3 &-3 &-3 &-2 & 1\\ | ||
| + | \end{array}</math> | ||
| + | |||
| + | |||
---- | ---- | ||
| Line 154: | Line 256: | ||
</math> | </math> | ||
| − | Therefore the filter can be | + | Therefore the filter can be separated into two 1-D filters. |
<math>h_1[m] = -\frac{1}{4}\delta[m+1] + \delta[m] -\frac{1}{4}\delta[m-1]</math> | <math>h_1[m] = -\frac{1}{4}\delta[m+1] + \delta[m] -\frac{1}{4}\delta[m-1]</math> | ||
| Line 205: | Line 307: | ||
<math>g[m,n]**h[m,n]: | <math>g[m,n]**h[m,n]: | ||
| + | \frac{1}{9} X | ||
\begin{array}{cccccccccccc} | \begin{array}{cccccccccccc} | ||
| − | 0 & 0 & 0 & 0 & | + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ |
| − | + | 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |
| − | 0 & 0 & - | + | 0 & 0 &-1 & 3 & 2 & 2 & 2 & 3 &-1 & 0 & 0\\ |
| − | 0 & - | + | 0 &-1 & 1 & 8 & 6 & 6 & 6 & 8 & 1 &-1 & 0\\ |
| − | - | + | -1& 1 & 7 & 9 & 8 & 8 & 8 & 9 & 7 & 1 &-1\\ |
| − | - | + | -3& 8 & 9 & 8 & 8 & 8 & 8 & 8 & 9 & 8 &-3\\ |
| − | - | + | -4&12 & 8 & 8 & 8 & 8 & 8 & 8 & 8 &12 &-4\\ |
| − | - | + | -4&12 & 8 & 8 & 8 & 8 & 8 & 8 & 8 &12 &-4\\ |
| − | - | + | -4&12 & 8 & 8 & 8 & 8 & 8 & 8 & 8 &12 &-4\\ |
| − | - | + | -3& 9 & 6 & 6 & 6 & 6 & 6 & 6 & 6 & 9 &-3\\ |
| − | - | + | -1& 3 & 2 & 2 & 2 & 2 & 2 & 2 & 2 & 3 &-1\\ |
| − | \end{array}</math> | + | \end{array} </math> |
Latest revision as of 15:07, 2 December 2014
Contents
Homework 11, ECE438, Fall 2014, Prof. Boutin
Question 1
Consider the following filter:
$ h[m,n]: \begin{array}{cccc} & m=-1 & m=0 & m=1 \\ n=1&\frac{1}{16} & \frac{2}{16} & \frac{1}{16} \\ n=0&\frac{2}{16} & \frac{4}{16} & \frac{2}{16} \\ n=-1&\frac{1}{16} & \frac{2}{16} & \frac{1}{16} \end{array} $
a) Write a difference equation that can be used to implement this filter.
$ \begin{align} y[m,n] =& \frac{1}{16}(x[m+1,n-1] + 2x[m,n-1] + x[m-1,n-1] \\ & + 2x[m+1,n] + 4x[m,n] + 2x[m-1,n] \\ & + x[m+1,n+1] + 2x[m,n+1] + x[m-1,n+1]) \end{align} $
b) Is this filter separable? Answer yes/no and justify your answer.
Yes. The coefficient matrix of h[m,n] can be written as product of two vectors.
$ \begin{pmatrix} \frac{1}{16} & \frac{2}{16} & \frac{1}{16} \\ \frac{2}{16} & \frac{4}{16} & \frac{2}{16} \\ \frac{1}{16} & \frac{2}{16} & \frac{1}{16} \end{pmatrix} = \begin{pmatrix} \frac{1}{4} \\ \frac{2}{4} \\ \frac{1}{4} \end{pmatrix} \cdot \begin{pmatrix} \frac{1}{4} & \frac{2}{4} & \frac{1}{4} \end{pmatrix} $
Therefore the filter can be decomposed to two 1-D filters.
$ h_1[m] = \frac{1}{4}(\delta[m+1] + 2\delta[m] +\delta[m-1]) $
$ h_2[n] = \frac{1}{4}(\delta[n+1] + 2\delta[n] +\delta[n-1]) $
c) Compute the DSFT H(u,v) of this filter. Sketch the plot of H(u,0). Sketch the plot of H(0,v). What are the characteristics of this filter (low-pass, band-pass, or high-pass)?
$ H_1(\mu) = DTFT\{h_1[m]\} = \frac{1}{4}(e^{j\mu} + 2 + e^{-j\mu}) = \frac{1}{2}(1 + cos\mu) $
$ H_2(\nu) = DTFT\{h_2[n]\} = \frac{1}{4}(e^{j\nu} + 2 + e^{-j\nu}) = \frac{1}{2}(1 + cos\nu) $
Using the separability,
$ H(\mu, \nu) = DSFT\{ h[m,n]\} = H_1(\mu)\cdot H_2(\nu) = \frac{1}{4}(1 + cos\mu)(1 + cos\nu) $
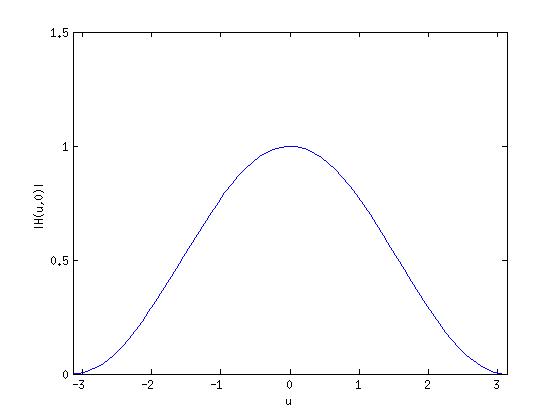
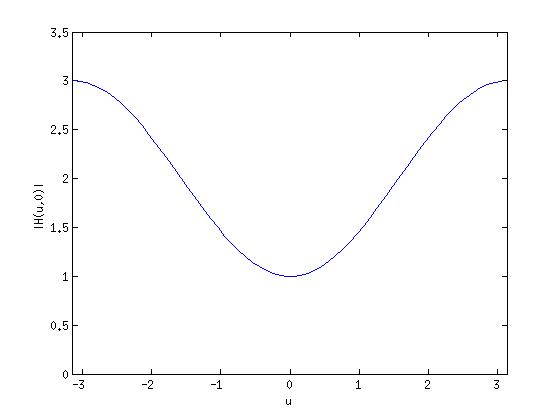
$ H(\mu, 0) = \frac{1}{2}(1 + cos\mu) $
So, $ H(\mu, 0) $ is a low-pass filter.
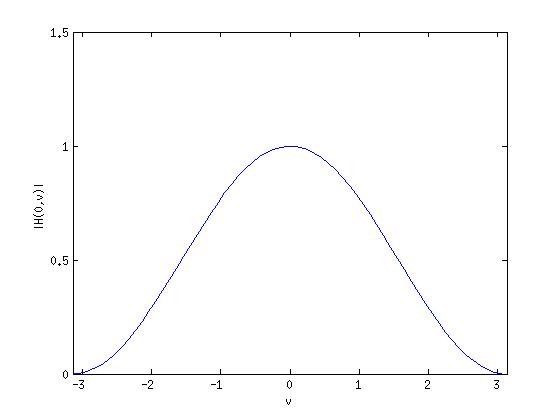
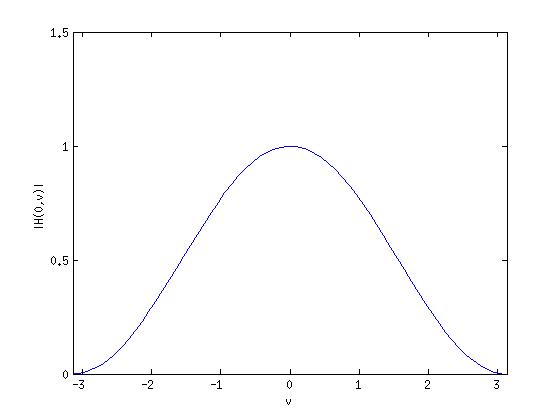
$ H(0, \nu) = \frac{1}{2}(1+cos\nu) $
So, $ H(0, \nu) $ is a low-pass filter.
d) What is the output image when this filter is applied to the following image (using symmetric boundary conditions)?
$ g[m,n]: \begin{array}{ccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{array} $
$ g[m,n]**h[m,n]: \frac{1}{16} X \begin{array}{cccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & 3 & 4 & 4 & 4 & 4 & 4 & 4 & 4 & 3 & 1\\ 3 & 9 &12 &12 &12 &12 &12 &12 &12 & 9 & 3\\ 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ 4 &12 &16 &16 &16 &16 &16 &16 &16 &12 & 4\\ 3 & 9 &12 &12 &12 &12 &12 &12 &12 & 9 & 3\\ 1 & 3 & 4 & 4 & 4 & 4 & 4 & 4 & 4 & 3 & 1\\ \end{array} $
Question 2
Consider the following filter:
$ h[m,n]: \begin{array}{cccc} & m=-1 & m=0 & m=1 \\ n=1&-\frac{1}{9} & -\frac{1}{9} & -\frac{1}{9} \\ n=0&-\frac{1}{9} & -\frac{8}{9} & -\frac{1}{9} \\ n=-1&-\frac{1}{9} &- \frac{1}{9} & -\frac{1}{9} \end{array} $
a) Write a difference equation that can be used to implement this filter.
$ \begin{align} y[m,n] =& -\frac{1}{9}(x[m+1,n-1] + x[m,n-1] + x[m-1,n-1] \\ & + x[m+1,n] + 8 x[m,n] + x[m-1,n] \\ & + x[m+1,n+1] + x[m,n+1] + x[m-1,n+1]) \end{align} $
b) Is this filter separable? Answer yes/no and justify your answer.
No. The coefficient matrix of h[m,n] cannot be decomposed to two vectors.
c) Compute the DSFT H(u,v) of this filter. Sketch the plot of H(u,0). Sketch the plot of H(0,v). What are the characteristics of this filter (low-pass, band-pass, or high-pass)?
$ \begin{align} H(\mu, \nu) = DTFT\{h[m,n]\} =& -\frac{1}{9} (e^{j(\mu-\nu)} + e^{j(-\nu)} + e^{j(-\mu-\nu)} \\ & + e^{j(\mu)} + 8 e^{(0)} + e^{j(-\mu)} \\ & + e^{j(\mu+\nu)} + e^{j(\nu)} + e^{j(-\mu+\nu)} ) \end{align} $
$ \begin{align} H(\mu, 0) =& -\frac{1}{9}( e^{j\mu} + e^{-j\nu} \\ & + e^{j\mu} + 8 + e^{-j\nu} \\ & + e^{j\mu} + e^{-j\nu} ) \\ =& -\frac{1}{9}(8+6cos{\mu}) \end{align} $
$ \begin{align} H(0, \nu) =& -\frac{1}{9} (e^{-j\nu} + e^{-j\nu} + e^{-j\nu} \\ & + 8 \\ & + e^{j\nu} + e^{j\nu} + e^{j\nu}) \\ =& -\frac{1}{9}(8+6cos{\mu}) \end{align} $
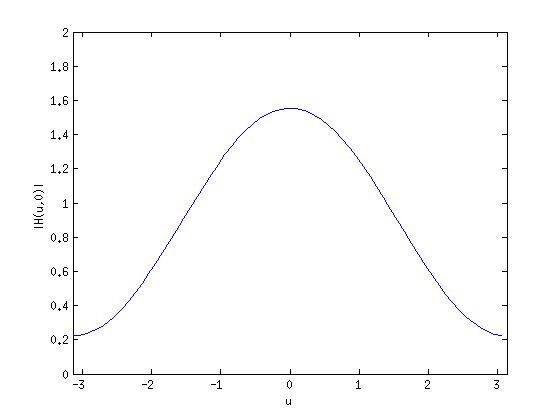
$ |H(\mu, 0)| = \frac{1}{9}(8+6cos{\mu}) $
So, $ H(\mu, 0) $ is a high-pass filter.
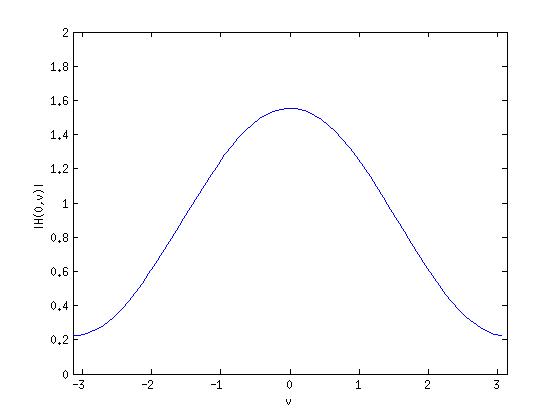
$ |H(0, \nu)| = \frac{1}{9}(8+6cos{\nu}) $
So, $ H(0, \nu) $ is a high-pass filter.
d) What is the output image when this filter is applied to the following image (using symmetric boundary conditions)?
$ g[m,n]: \begin{array}{ccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{array} $
$ g[m,n]**h[m,n]: \frac{1}{9} X \begin{array}{cccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ -1&-2 &-3 &-3 &-3 &-3 &-3 &-3 &-3 &-2 & 1\\ -2& 5 & 3 & 3 & 3 & 3 & 3 & 3 & 3 & 5 &-2\\ -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ -3& 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 &-3\\ -2& 5 & 3 & 3 & 3 & 3 & 3 & 3 & 3 & 5 &-2\\ -1&-2 &-3 &-3 &-3 &-3 &-3 &-3 &-3 &-2 & 1\\ \end{array} $
Question 3
Consider the following filter:
$ h[m,n]: \begin{array}{cccc} & m=-1 & m=0 & m=1 \\ n=1&-\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \\ n=0&-\frac{1}{4} & 1 & -\frac{1}{4} \\ n=-1&-\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \end{array} $
a) Write a difference equation that can be used to implement this filter.
$ \begin{align} y[m,n] =& -\frac{1}{8}x[m+1,n-1] + \frac{1}{2}x[m,n-1] - \frac{1}{8}x[m-1,n-1] \\ & -\frac{1}{4}x[m+1,n] + x[m,n] -\frac{1}{4}x[m-1,n] \\ & -\frac{1}{8}x[m+1,n+1] + \frac{1}{2}x[m,n+1] -\frac{1}{8}x[m-1,n+1] \end{align} $
b) Is this filter separable? Answer yes/no and justify your answer.
Yes. The coefficient matrix of h[m,n] can be written as product of two vectors.
$ \begin{pmatrix} -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \\ -\frac{1}{4} & 1 & -\frac{1}{4} \\ -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ 1 \\ \frac{1}{2} \end{pmatrix} \cdot \begin{pmatrix} -\frac{1}{4} & 1 & -\frac{1}{4} \end{pmatrix} $
Therefore the filter can be separated into two 1-D filters.
$ h_1[m] = -\frac{1}{4}\delta[m+1] + \delta[m] -\frac{1}{4}\delta[m-1] $
$ h_2[n] = \frac{1}{2}\delta[n+1] + \delta[n] +\frac{1}{2}\delta[n-1] $
c) Compute the DSFT H(u,v) of this filter. Sketch the plot of H(u,0). Sketch the plot of H(0,v). What are the characteristics of this filter (low-pass, band-pass, or high-pass)?
$ H_1(\mu) = DTFT\{h_1[m]\} = -\frac{1}{4}e^{-j\mu(-1)} + e^{-j\mu(0)} -\frac{1}{4}e^{-j\mu(1)} = 1-\frac{1}{2}cos\mu $
$ H_2(\nu) = DTFT\{h_2[n]\} = \frac{1}{2}e^{-j\nu(-1)} + e^{-j\nu(0)} +\frac{1}{2}e^{-j\nu(1)} = 1+cos\nu $
Using the separability,
$ H(\mu, \nu) = DSFT\{ h[m,n]\} = H_1(\mu)\cdot H_2(\nu) = (1-\frac{1}{2}cos\mu)(1+cos\nu) $
$ H(\mu, 0) = 2(1-\frac{1}{2}cos\mu) $
So, $ H(\mu, 0) $ is a high-pass filter.
$ H(0, \nu) = \frac{1}{2}(1+cos\nu) $
So, $ H(0, \nu) $ is a low-pass filter.
d) What is the output image when this filter is applied to the following image (using symmetric boundary conditions)?
$ g[m,n]: \begin{array}{ccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{array} $
$ g[m,n]**h[m,n]: \frac{1}{9} X \begin{array}{cccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 &-1 & 3 & 2 & 2 & 2 & 3 &-1 & 0 & 0\\ 0 &-1 & 1 & 8 & 6 & 6 & 6 & 8 & 1 &-1 & 0\\ -1& 1 & 7 & 9 & 8 & 8 & 8 & 9 & 7 & 1 &-1\\ -3& 8 & 9 & 8 & 8 & 8 & 8 & 8 & 9 & 8 &-3\\ -4&12 & 8 & 8 & 8 & 8 & 8 & 8 & 8 &12 &-4\\ -4&12 & 8 & 8 & 8 & 8 & 8 & 8 & 8 &12 &-4\\ -4&12 & 8 & 8 & 8 & 8 & 8 & 8 & 8 &12 &-4\\ -3& 9 & 6 & 6 & 6 & 6 & 6 & 6 & 6 & 9 &-3\\ -1& 3 & 2 & 2 & 2 & 2 & 2 & 2 & 2 & 3 &-1\\ \end{array} $
Discussion
You may discuss the homework below.
- write comment/question here
- answer will go here