| Line 37: | Line 37: | ||
*When we sampled a signal in the time domain, we usually sample a continuous time signal. However, we can't just sample the signal without discreeting the points within the continuous time signal. The reason for this is because, each discreet points within the continuous time signal will be the sampled points of the sampled signal in the frequency domain. The graphical interpretation for this relationship can be seen in the picture below | *When we sampled a signal in the time domain, we usually sample a continuous time signal. However, we can't just sample the signal without discreeting the points within the continuous time signal. The reason for this is because, each discreet points within the continuous time signal will be the sampled points of the sampled signal in the frequency domain. The graphical interpretation for this relationship can be seen in the picture below | ||
| + | [[Image:Sl2.jpg|500px|relationship view for the sampling signal between time domain and frequency domain]] | ||
---- | ---- | ||
Revision as of 10:20, 6 October 2014
Frequency domain view of the relationship between a signal and a sampling of that signal
A slecture by ECE student Talha Takleh Omar Takleh
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Outline
- Introduction
- Main Points
- Conclusion
Introduction
This Slecture will look into the relationship between a signal and the sampling of that signal in the view of the frequency domain. The signal that will be sampled will be in the time domain $ x(t) $ and after it was Fourier transformed, the sampled signal $ X(f) $ will be in the frequency domain. Here, we will see the relationship between this two signals and what rules need to be obeyed in order to create a good sampling signal within the frequency domain.
Main Points
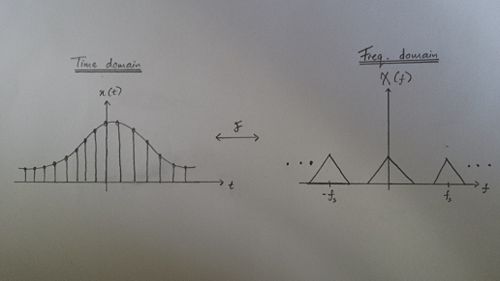
- The sampling of a signal in the time domain $ x(t) $ is basically the repetition of the sampled signal $ x(t) $ or the $ rep $ function in the frequency domain. The graphical interpretation for this relationship can be seen in the picture below
- From the picture above, I should point out that this relationship goes both ways, if we try to sample a signal from the frequency domain the sampled signal that will be produced in the time domain will also be in the form a of $ rep $ function.
- When we sampled a signal in the time domain, we usually sample a continuous time signal. However, we can't just sample the signal without discreeting the points within the continuous time signal. The reason for this is because, each discreet points within the continuous time signal will be the sampled points of the sampled signal in the frequency domain. The graphical interpretation for this relationship can be seen in the picture below