| Line 15: | Line 15: | ||
[[Image:438slecture_X.png]] | [[Image:438slecture_X.png]] | ||
| − | |||
[[Image:438slecture_X_s_2.png]] | [[Image:438slecture_X_s_2.png]] | ||
Revision as of 14:51, 4 October 2014
Slecture_Nyquist_Theorem_Stein
The Nyquist Theorem states that it is possible to reproduce a signal from sampled version of that signal given that the sampling frequency is greater than twice the greatest frequency component of the original signal.
Proof
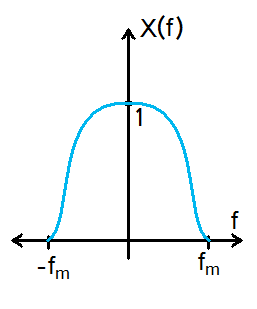
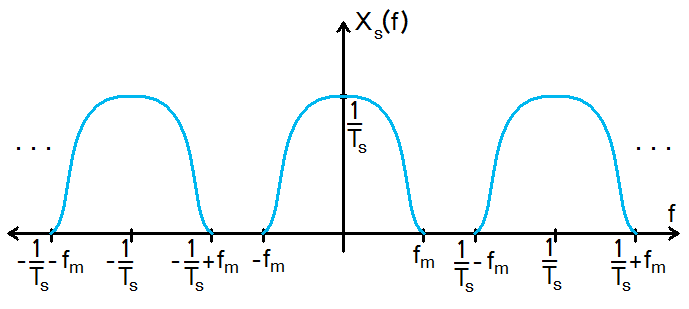
Let's begin by looking at X(f) and $ X_{s} $(f):
Observe that $ X_{s} $(f) consists of $ (1/T_{s}) $*X(f) repeated every $ 1/T_{s} $.
If we use a low-pass filter with gain $ T_{s} $ on $ X_{s} $(f), we can obtain the original signal if the repetitions don't overlap.
For this case to be met, $ 1/T_{s} - f_{m} $ must be greater than $ f_{m} $.
In other words,
$ \frac{1}{T_{s}} > 2f_{m} $