| Line 1: | Line 1: | ||
<br> | <br> | ||
| − | == | + | == Limits of Functions == |
by: [[User:Yehm|Michael Yeh]], proud Member of [[Math squad|the Math Squad]]. | by: [[User:Yehm|Michael Yeh]], proud Member of [[Math squad|the Math Squad]]. | ||
| − | <pre> keyword: tutorial, limit, function, sequence </pre> | + | <pre> keyword: tutorial, limit, function, sequence </pre> |
| − | '''INTRODUCTION''' Provided here is a brief introduction to the concept of "limit," which features prominently in calculus. We first discuss the limit of a function at a point; to help motivate the definition, we first consider continuous functions. Unless otherwise mentioned, all functions here will have domain and range <math>\mathbb{R}</math>, the real numbers. Words such as "all," "every," "each," "some," and "there are" are quite important here; read carefully! | + | |
| + | '''INTRODUCTION''' | ||
| + | |||
| + | Provided here is a brief introduction to the concept of "limit," which features prominently in calculus. We first discuss the limit of a function at a point; to help motivate the definition, we first consider continuous functions. Unless otherwise mentioned, all functions here will have domain and range <math>\mathbb{R}</math>, the real numbers. Words such as "all," "every," "each," "some," and "there are" are quite important here; read carefully! | ||
== Continuous functions == | == Continuous functions == | ||
Revision as of 13:10, 11 May 2014
Contents
Limits of Functions
by: Michael Yeh, proud Member of the Math Squad.
keyword: tutorial, limit, function, sequence
INTRODUCTION
Provided here is a brief introduction to the concept of "limit," which features prominently in calculus. We first discuss the limit of a function at a point; to help motivate the definition, we first consider continuous functions. Unless otherwise mentioned, all functions here will have domain and range $ \mathbb{R} $, the real numbers. Words such as "all," "every," "each," "some," and "there are" are quite important here; read carefully!
Continuous functions
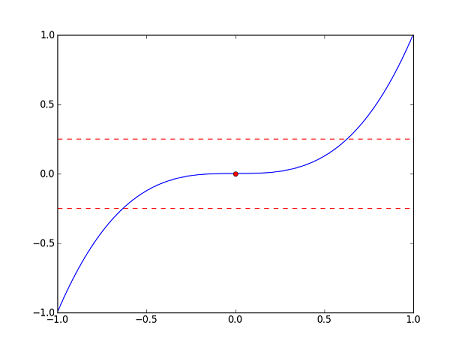
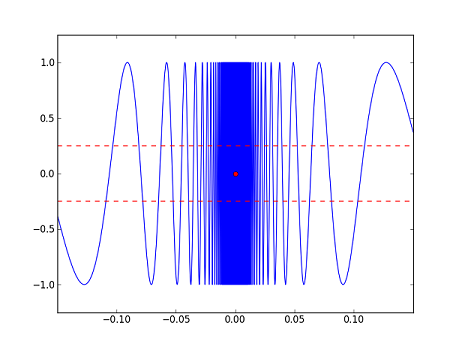
Let's consider the the following three functions along with their graphs (in blue). The red dots in each correspond to $ x=0 $, e.g. for $ f $, the red dot is the point $ (0,f(0))=(0,0) $.
- $ \displaystyle f(x)=x^3 $
- $ g(x)=\begin{cases}-x^2-\frac{1}{2} &\text{if}~x<0\\ x^2+\frac{1}{2} &\text{if}~x\geq 0\end{cases} $
- $ h(x)=\begin{cases} \sin\left(\frac{1}{x}\right) &\text{if}~x\neq 0\\ 0 &\text{if}~x=0\end{cases} $
We can see from the graphs that $ f $ is "continuous" at $ 0 $, and that $ g $ and $ h $ are "discontinuous" at 0. But, what exactly do we mean? Intuitively, $ f $ seems to be continuous at $ 0 $ because $ f(x) $ is close to $ f(0) $ whenever $ x $ is close to $ 0 $. On the other hand, $ g $ appears to be discontinuous at $ 0 $ because there are points $ x $ which are close to $ 0 $ but such that $ g(x) $ is far away from $ g(0) $. The same observation applies to $ h $.
Let's make these observations more precise. First, we will try to estimate $ f(0) $ with error at most $ 0.25 $, say. In the graph of $ f $, we have marked off a band of width $ 0.5 $ about $ f(0) $. So, any point in the band will provide a good approximation here. As a first try, we might think that if $ x $ is close enough to $ 0 $, then $ f(x) $ will be a good estimate of $ f(0) $. Indeed, we see from the graph that for any $ x $ in the interval $ (-\sqrt[3]{0.25},\sqrt[3]{0.25}) $, $ f(x) $ lies in the band (or if we wish to be more pedantic, we would say that $ (x,f(x)) $ lies in the band). So, "close enough to $ 0 $" here means in the interval $ (-\sqrt[3]{0.25},\sqrt[3]{0.25}) $; note that any point which is close enough to $ 0 $ provides a good approximation of $ f(0) $.
Can we do the same for $ g $?
TOPIC 3
Lorem Ipsum [1] is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
TOPIC 2
Lorem Ipsum [1] is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
REFERENCES
[1] "Loream Ipsum" <http://www.lipsum.com/>.
Questions and comments
If you have any questions, comments, etc. please, please please post them below:
- Comment / question 1
- Comment / question 2
The Spring 2013 Math Squad 2013 was supported by an anonymous gift to Project Rhea. If you enjoyed reading these tutorials, please help Rhea "help students learn" with a donation to this project. Your contribution is greatly appreciated.