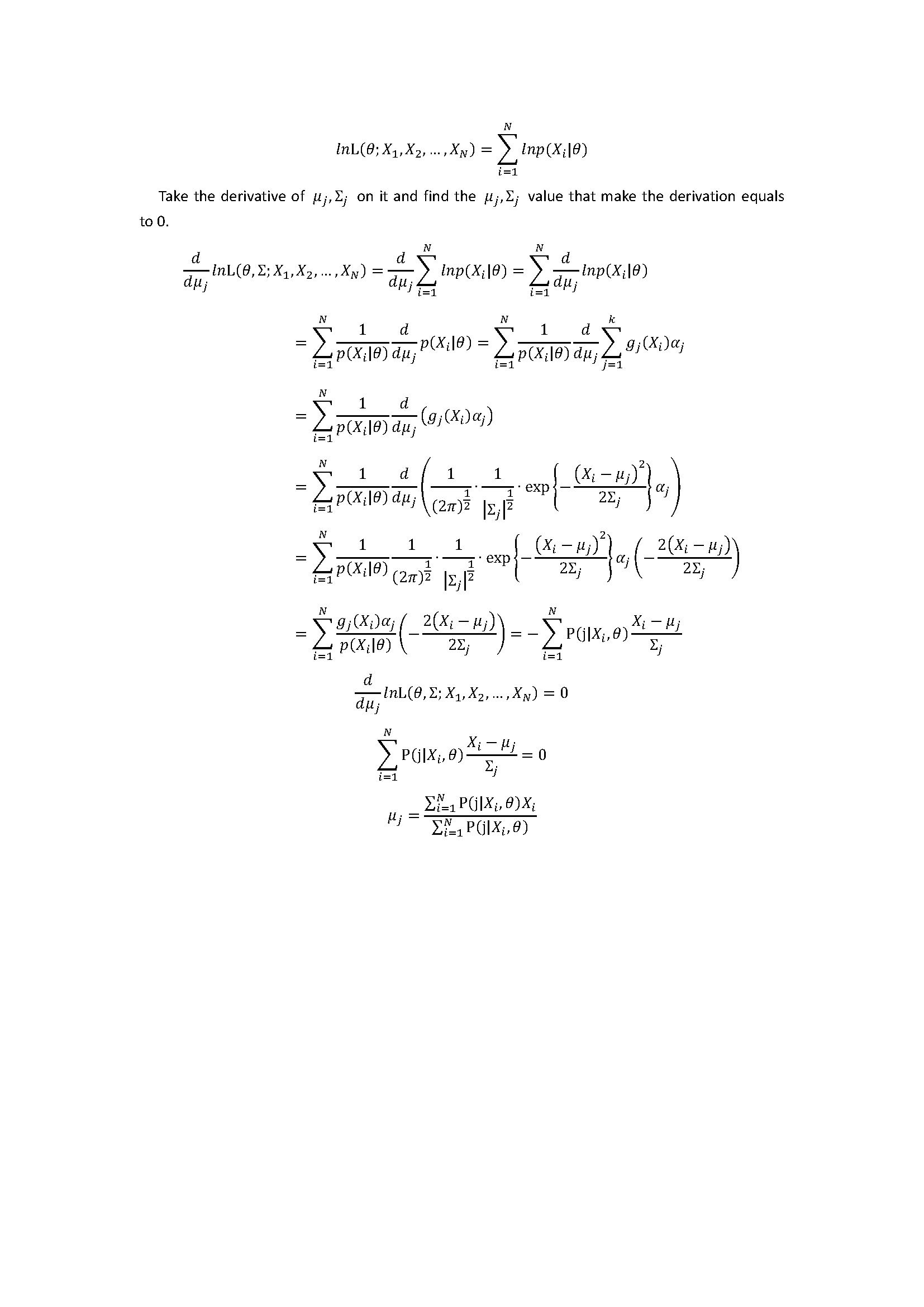m (Have great difficulty in pasting formula...)
 
m (Got great difficult in showing formulas....)
Line 11: Line 11:
 
----
 
----
  
−
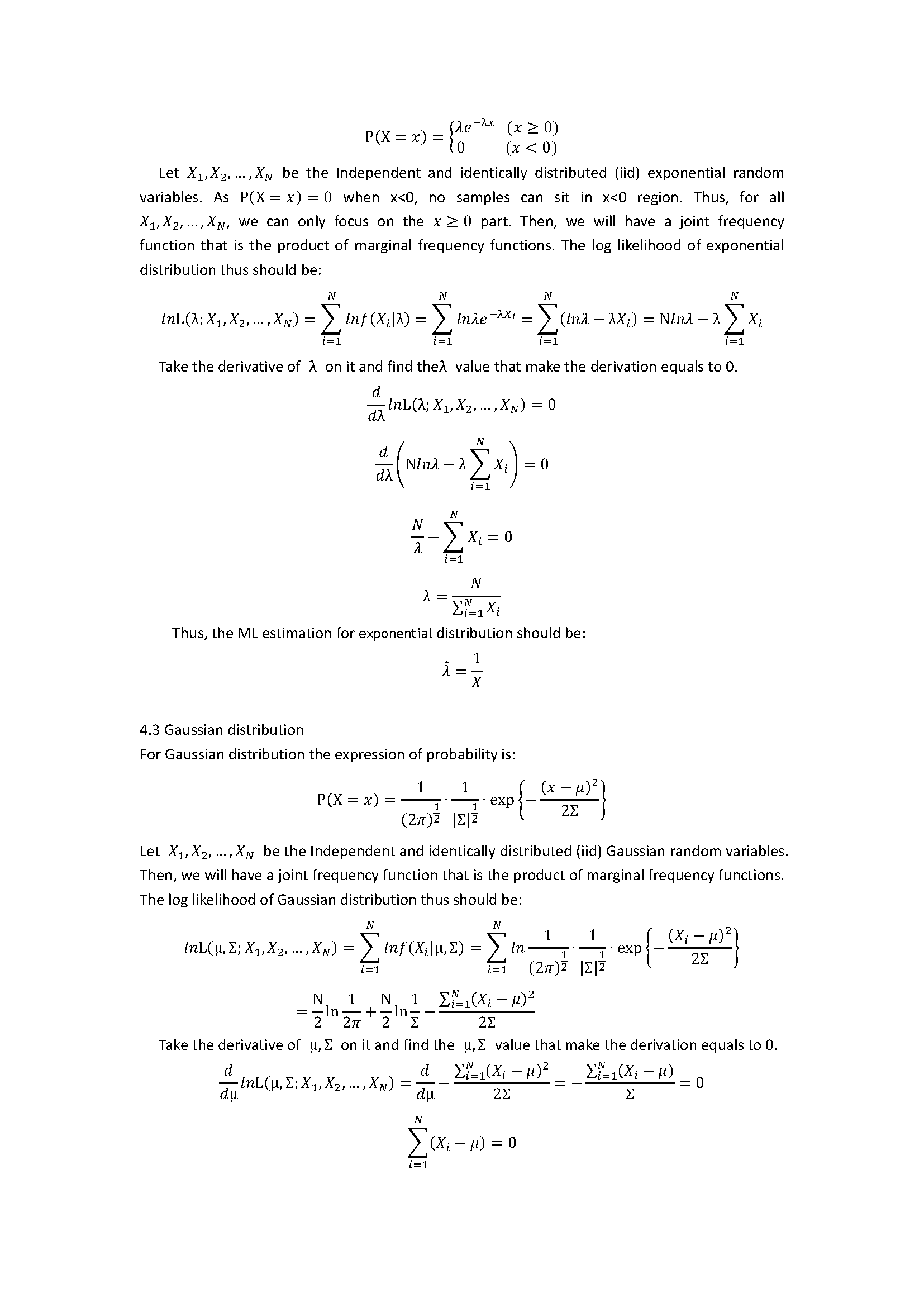
<span lang="EN-US" style="font-size:14.0pt">&nbsp;</span>  
+
<span lang="EN-US" style="font-size:14.0pt">&nbsp;[[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_1.png|frame|center]]</span>  
  
−
<span lang="EN-US" style="font-size:14.0pt">&nbsp;</span>  
+
<span lang="EN-US" style="font-size:14.0pt">&nbsp;[[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_2.png|frame|center]]</span>  
  
 
<span lang="EN-US">&nbsp;</span>  
 
<span lang="EN-US">&nbsp;</span>  
  
−
<br>  
+
[[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_3.png|frame|center]]<br>  
  
−
'''<span lang="EN-US" style="font-size:12.0pt">1. Introduction</span>'''
+
[[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_4.png|frame|center]][[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_5.png|frame|center]][[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_6.png|frame|center]][[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_7.png|frame|center]][[Image:Introduction_to_Maximum_Likelihood_Estimation_Page_8.png|frame|center]]<br>
−
 
+
−
<span lang="EN-US">In statistics,
+
−
maximum-likelihood estimation (MLE) is a method of estimating the parameters of
+
−
a statistical model. When applied to a data set and given a statistical model,
+
−
maximum-likelihood estimation provides estimates for the model's parameters.</span>
+
−
 
+
−
<span lang="EN-US">In maximum
+
−
likelihood estimation, we search over all possible sets of parameter values for
+
−
a specified model to find the set of values for which the observed sample was
+
−
most likely. That is, we find the set of parameter values that, given a model,
+
−
were most likely to have given us the data that we have in hand.</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
'''<span lang="EN-US" style="font-size:12.0pt">2. Basic method</span>'''<br>
+
−
 
+
−
<span lang="EN-US">Suppose there is
+
−
a sample <math>x_1,\ x_2,\ \dots ,\ x_N</math> of n independent and identically distributed observations from
+
−
a distribution with an unknown probability density function <span class="texhtml">''f''<sub>0</sub></span>. We can say that the function </span><span lang="EN-US">&lt;img width=12 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image002.png"&gt;</span><span lang="EN-US">&nbsp;belongs to a certain family of distributions </span><span lang="EN-US">&lt;img width=96 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image003.png"&gt;</span><span lang="EN-US">, where θ is a vector of parameters for this family, so that so that
+
−
</span><span lang="EN-US">&lt;img width=76 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image004.png"&gt;</span><span lang="EN-US">. The value </span><span lang="EN-US">&lt;img width=14 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image005.png"&gt;</span><span lang="EN-US">&nbsp;is unknown and is referred to as the true value of the
+
−
parameter. So, using MLE, we want to find an estimator which would be as close
+
−
to the true value </span><span lang="EN-US">&lt;img width=14 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image005.png"&gt;</span><span lang="EN-US">&nbsp;as possible.</span>
+
−
 
+
−
<span lang="EN-US">To use the
+
−
method of maximum likelihood, one first specifies the joint density function
+
−
for all observations. For an independent and identically distributed sample,
+
−
this joint density function is</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=347 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image006.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">As each sample </span><span lang="EN-US">&lt;img width=12 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image007.png"&gt;</span><span lang="EN-US">&nbsp;is independent with each other, the likelihood of </span><span lang="EN-US">&lt;img width=8 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image008.png"&gt;</span><span lang="EN-US">&nbsp;with the observation of samples </span><span lang="EN-US">&lt;img width=70 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image009.png"&gt;</span><span lang="EN-US">&nbsp;can be defined as:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=315 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image010.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">In practice, it’s
+
−
more convenient to take ln for the both sides, called log-likelihhod. Then the
+
−
formula becomes:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=216 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image011.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Then, for a
+
−
fixed set of samples, to maximize the likelihood of </span><span lang="EN-US">&lt;img width=8 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image008.png"&gt;</span><span lang="EN-US">, we should choose the data that satisfied:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=397 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image012.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">To find the
+
−
maximum of </span><span lang="EN-US">&lt;img width=116 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image013.png"&gt;</span><span lang="EN-US">, we take the derivative of </span><span lang="EN-US">&lt;img width=8 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image008.png"&gt;</span><span lang="EN-US">&nbsp;on it and find the</span><span lang="EN-US">&lt;img width=8 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image008.png"&gt;</span><span lang="EN-US">&nbsp;value that make the derivation equals to 0.</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=161 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image014.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">To check our
+
−
result we should garentee that the second derivative of </span><span lang="EN-US">&lt;img width=8 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image008.png"&gt;</span><span lang="EN-US">&nbsp;on </span><span lang="EN-US">&lt;img width=115 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image015.png"&gt;</span><span lang="EN-US">&nbsp;is negative.</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=167 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image016.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
'''<span lang="EN-US" style="font-size:12.0pt">3. Practice</span>''' considerations
+
−
 
+
−
<span lang="EN-US">3.1 Log-likelihood</span>
+
−
 
+
−
<span lang="EN-US">Just as
+
−
mentioned above, to make life a little easier, we can work with the natural log
+
−
of likelihoods rather than the likelihoods themselves. The main reason for this
+
−
is, computational rather than theoretical. If you multiply lots of very small
+
−
numbers together (say all less than 0.0001) then you will very quickly end up
+
−
with a number that is too small to be represented by any calculator or computer
+
−
as different from zero. This situation will often occur in calculating
+
−
likelihoods, when we are often multiplying the probabilities of lots of rare
+
−
but independent events together to calculate the joint probability.</span>
+
−
 
+
−
<span lang="EN-US">With
+
−
log-likelihoods, we simply add them together rather than multiply them
+
−
(log-likelihoods will always be negative, and will just get larger (more
+
−
negative) rather than approaching 0).</span>
+
−
 
+
−
<span lang="EN-US">So,
+
−
log-likelihoods are conceptually no different to normal likelihoods. When we optimize
+
−
the log-likelihood, with respect to the model parameters, we also optimize the
+
−
likelihood with respect to the same parameters, for there is a one-to-one
+
−
(monotonic) relationship between numbers and their logs.</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
<span lang="EN-US">3.2 Removing the constant</span>
+
−
 
+
−
<span lang="EN-US">For example the
+
−
likelihood function for the binomial distribution is:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=175 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image017.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">In the context
+
−
of MLE, we noted that the values representing the data will be fixed: these are
+
−
''n'' and'' k''. In this case, the binomial 'co-efficient' depends only
+
−
upon these constants. Because it does not depend on the value of the parameter ''p''
+
−
we can essentially ignore this first term. This is because any value for ''p''
+
−
which maximizes the above quantity will also maximize</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=80 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image018.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">This means that
+
−
the likelihood will have no meaningful scale in and of itself. This is not
+
−
usually important, however, for as we shall see, we are generally interested
+
−
not in the absolute value of the likelihood but rather in the ''ratio ''between
+
−
two likelihoods - in the context of a likelihood ratio test.</span>
+
−
 
+
−
<span lang="EN-US">We may often
+
−
want to ignore the parts of the likelihood that do not depend upon the
+
−
parameters in order to reduce the computational intensity of some problems.
+
−
Even in the simple case of a binomial distribution, if the number of trials
+
−
becomes very large, the calculation of the factorials can become infeasible.</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
<span lang="EN-US">3.3 Numerical MLE</span>
+
−
 
+
−
<span lang="EN-US">Sometimes we cannot write an equation that
+
−
can be differentiated to find the MLE parameter estimates. This is especially
+
−
likely if the model is complex and involves many parameters and/or complex
+
−
probability functions. (e.g. the normal mixture probability distribution)</span>
+
−
 
+
−
<span lang="EN-US">In this scenario, it is also typically not
+
−
feasible to evaluate the likelihood at all points, or even a reasonable number
+
−
of points. In the parameter space of the problem in the coin toss example, the
+
−
parameter space was only one-dimensional (i.e. only one parameter) and ranged
+
−
between 0 and 1. Nonetheless, because p can theoretically take any value
+
−
between 0 and 1, the MLE will always be an approximation (albeit an incredibly
+
−
accurate one) if we just evaluate the likelihood for a finite number of
+
−
parameter values. For example, we chose to evaluate the likelihood at steps of
+
−
0.02. But we could have chosen steps of 0.01, of 0.001, of 0.000000001, etc. In
+
−
theory and practice, one has to set a minimum tolerance by which you are happy
+
−
for your estimates to be out. This is why computers are essential for these
+
−
types of problems: they can tabulate lots and lots of values very quickly and
+
−
therefore achieve a much finer resolution.</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
'''<span lang="EN-US" style="font-size:12.0pt">4. Some basic examples</span>'''
+
−
 
+
−
<span lang="EN-US">4.1 Poisson Distribution</span>
+
−
 
+
−
<span lang="EN-US">For Poisson
+
−
distribution the expression of probability is:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=108 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image019.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Let </span><span lang="EN-US">&lt;img width=75 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image020.png"&gt;</span><span lang="EN-US">&nbsp;be the Independent and identically distributed (iid) Poisson random
+
−
variables. Then, we will have a joint frequency function that is the product of
+
−
marginal frequency functions. The log likelihood of Poisson distribution thus
+
−
should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=554 height=125
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image021.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Take the derivative
+
−
of </span><span lang="EN-US">&lt;img width=7 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image022.png"&gt;</span><span lang="EN-US">&nbsp;on it and find the</span><span lang="EN-US">&lt;img width=7 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image022.png"&gt;</span><span lang="EN-US">&nbsp;value that make the derivation equals to 0.</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=162 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image023.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=217 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image024.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=95 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image025.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=68 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image026.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Thus, the ML
+
−
estimation for Poisson distribution should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=35 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image027.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
<span lang="EN-US">4.2 Exponential distribution</span>
+
−
 
+
−
<span lang="EN-US">For exponential distribution the expression
+
−
of probability is:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=167 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image028.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Let </span><span lang="EN-US">&lt;img width=75 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image020.png"&gt;</span><span lang="EN-US">&nbsp;be the Independent and identically distributed (iid)
+
−
exponential random variables. As </span><span lang="EN-US">&lt;img width=80 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image029.png"&gt;</span><span lang="EN-US">&nbsp;when x&lt;0, no samples can sit in x&lt;0 region. Thus, for
+
−
all </span><span lang="EN-US">&lt;img width=75 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image020.png"&gt;</span><span lang="EN-US">, we can only focus on the </span><span lang="EN-US">&lt;img width=34 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image030.png"&gt;</span><span lang="EN-US">&nbsp;part. Then, we will have a joint frequency function that is
+
−
the product of marginal frequency functions. The log likelihood of exponential
+
−
distribution thus should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=517 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image031.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Take the derivative
+
−
of </span><span lang="EN-US">&lt;img width=7 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image022.png"&gt;</span><span lang="EN-US">&nbsp;on it and find the</span><span lang="EN-US">&lt;img width=7 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image022.png"&gt;</span><span lang="EN-US">&nbsp;value that make the derivation equals to 0.</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=162 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image023.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=149 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image032.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=87 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image033.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=67 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image034.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Thus, the ML
+
−
estimation for </span><span lang="EN-US">exponential</span><span lang="EN-US"> distribution
+
−
should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=35 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image035.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
<span lang="EN-US">4.3 Gaussian distribution</span>
+
−
 
+
−
<span lang="EN-US">For Gaussian distribution the expression of
+
−
probability is:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=249 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image036.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Let </span><span lang="EN-US">&lt;img width=75 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image020.png"&gt;</span><span lang="EN-US">&nbsp;be the Independent and identically distributed (iid) Gaussian random
+
−
variables. Then, we will have a joint frequency function that is the product of
+
−
marginal frequency functions. The log likelihood of Gaussian distribution thus
+
−
should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=554 height=104
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image037.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Take the derivative
+
−
of </span><span lang="EN-US">&lt;img width=21 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image038.png"&gt;</span><span lang="EN-US">&nbsp;on it and find the </span><span lang="EN-US">&lt;img width=21 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image038.png"&gt;</span><span lang="EN-US">&nbsp;value that make the derivation equals to 0.</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=417 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image039.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=94 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image040.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=68 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image041.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=491 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image042.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=108 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image043.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Thus, the ML
+
−
estimation for </span><span lang="EN-US">Gaussian</span><span lang="EN-US"> distribution
+
−
should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=36 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image044.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=110 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image045.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
'''<span lang="EN-US" style="font-size:12.0pt">5. Some</span>''' advanced examples
+
−
 
+
−
<span lang="EN-US">5.1 Expression of Estimated Parameters</span>
+
−
 
+
−
<span lang="EN-US">The above
+
−
estimation all base on the assumption that the distribution to be estimated follows
+
−
the distribution of a single function, but how about the estimation of the mixture
+
−
of functions?</span>
+
−
 
+
−
<span lang="EN-US">To simplify the problem,
+
−
we only talk about Gaussian Mixture Model (GMM) here. Using the same method, it’s
+
−
easy to extend it to other kind of mixture model and the mixture between
+
−
different models.</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; To
+
−
start with, we should know that if we set the number of Gaussian function to be
+
−
used in the GMM estimation flexible, we will find out that the number of Gaussian
+
−
function will never reach a best solution, as adding more Gaussian functions
+
−
into the estimation will subsequently improve the accuracy anyway. As
+
−
calculating how many Gaussian function is include in GMM is a clustering
+
−
problem. We assume to know the number of Gaussian function in GMM as k here.</span>
+
−
 
+
−
<span lang="EN-US">As this
+
−
distribution is a mixture of Gaussian, the expression of probability is:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=139 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image046.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img width=13 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image047.png"&gt;</span><span lang="EN-US">&nbsp;is the weight of Gaussian function </span><span lang="EN-US">&lt;img width=33 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image048.png"&gt;</span><span lang="EN-US">. </span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=237 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image049.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
<span lang="EN-US">Thus, the
+
−
parameters to be estimated are:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=263 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image050.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Let </span><span lang="EN-US">&lt;img width=75 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image020.png"&gt;</span><span lang="EN-US">&nbsp;be the Independent and identically distributed (iid) Gaussian
+
−
Mixture Model (GMM) random variables. </span>
+
−
 
+
−
<span lang="EN-US">Following Bayes
+
−
rule, the responsibility that a mixture component takes for explaining an
+
−
observation </span><span lang="EN-US">&lt;img width=13 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image051.png"&gt;</span><span lang="EN-US">&nbsp;is:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=264 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image052.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Then, we will
+
−
have a joint frequency function that is the product of marginal frequency
+
−
functions. The log likelihood of Gaussian Mixture Model distribution thus
+
−
should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=217 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image053.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Take the derivative
+
−
of </span><span lang="EN-US">&lt;img width=31 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image054.png"&gt;</span><span lang="EN-US">&nbsp;on it and find the </span><span lang="EN-US">&lt;img width=31 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image054.png"&gt;</span><span lang="EN-US">&nbsp;value that make the derivation equals to 0.</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=554 height=374
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image055.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=183 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image056.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=146 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image057.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=128 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image058.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=554 height=437
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image059.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=182 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image060.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=246 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image061.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=208 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image062.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=175 height=62
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image063.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; The
+
−
</span><span lang="EN-US">&lt;img width=16 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image064.png"&gt;</span><span lang="EN-US">is subject to </span><span lang="EN-US">&lt;img width=69 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image065.png"&gt;</span><span lang="EN-US">. Basic optimization theories show that </span><span lang="EN-US">&lt;img width=13 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image047.png"&gt;</span><span lang="EN-US">&nbsp;</span><span lang="EN-US">&lt;img width=97 height=21
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image066.png"&gt;</span><span lang="EN-US">:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img
+
−
width=114 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image067.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">Thus, the ML
+
−
estimation for </span><span lang="EN-US">Gaussian</span><span lang="EN-US"> Mixture Model
+
−
distribution should be:</span>
+
−
 
+
−
<span lang="EN-US">&lt;img width=104 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image068.png"&gt;</span><span lang="EN-US">; </span><span lang="EN-US">&lt;img width=135 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image069.png"&gt;</span><span lang="EN-US">; </span><span lang="EN-US">&lt;img width=93 height=42
+
−
src="Introduction%20to%20Maximum%20Likelihood%20Estimation%20-%20copy.files/image070.png"&gt;</span>
+
−
 
+
−
<span lang="EN-US">&nbsp;</span>
+
−
 
+
−
<span lang="EN-US">5.2 Practical Implementation</span>
+
−
 
+
−
<span lang="EN-US">Now we can
+
−
observe that, as the Gaussian Mixture Model with K Gaussian functions have 3K
+
−
parameters, to find the best vector of parameters set, </span><span style="font-family:宋体">θ</span><span lang="EN-US">, is to find the optimized
+
−
parameters in 3K dimension space. As the Gaussian Mixture Model include more
+
−
Gaussian functions, the complexity of computing the best </span><span style="font-family:宋体">θ</span><span lang="EN-US"> will go incrediblily high.
+
−
Also, we can see that all the expressions of </span><span style="font-family: 宋体">μ</span><span lang="EN-US">, </span><span style="font-family:宋体">Σ</span><span lang="EN-US"> and </span><span style="font-family:宋体">α</span><span lang="EN-US">
+
−
include themselves directly or indirectly, it’s implossible to get the value of
+
−
the parameters within one time calculation.</span>
+
−
 
+
−
<span lang="EN-US">Now it’s time to
+
−
introduce a method for finding maximum likelihood with large number of latent variables
+
−
(parameters), Expectation–maximization (EM) algorithm.</span>
+
−
 
+
−
<span lang="EN-US">In statistics,
+
−
an expectation–maximization (EM) algorithm is an iterative method for finding maximum
+
−
likelihood estimates of parameters in statistical models, where the model
+
−
depends on unobserved latent variables (the parameters). The EM iteration
+
−
alternates between performing an expectation (E) step, which creates a function
+
−
for the expectation of the log-likelihood evaluated using the current estimate
+
−
for the parameters, and a maximization (M) step, which computes parameters
+
−
maximizing the expected log-likelihood found on the E step. These
+
−
parameter-estimates are then used to determine the distribution of the latent
+
−
variables in the next E step.</span>
+
−
 
+
−
<span lang="EN-US">In short words,
+
−
to get the best </span><span style="font-family:宋体">θ</span><span lang="EN-US">
+
−
for our maximum likelihood, firstly, for the expectation step, we should evaluate
+
−
the weight of each cluster with the current parameters. Then, for the
+
−
maximization step, we re-estimate parameters using the existing weight.</span>
+
−
 
+
−
<span lang="EN-US">By repeating
+
−
these calculation process for several times, the parameters will approach the
+
−
value for the maximum likelihood.</span>  
+
  
 
<span lang="EN-US">&nbsp;</span>  
 
<span lang="EN-US">&nbsp;</span>  
  
−
'''<span lang="EN-US" style="font-size:12.0pt">6. References</span>'''  
+
'''<span lang="EN-US" style="font-size:12.0pt">References</span>'''  
  
 
[http://www.cscu.cornell.edu/news/statnews/stnews50.pdf www.cscu.cornell.edu/news/statnews/stnews50.pdf]  
 
[http://www.cscu.cornell.edu/news/statnews/stnews50.pdf www.cscu.cornell.edu/news/statnews/stnews50.pdf]  

Revision as of 22:28, 30 April 2014


Introduction to Maximum Likelihood Estimation
A slecture by Wen Yi

pdf file:Introduction to Maximum Likelihood Estimation.pdf


 
Introduction to Maximum Likelihood Estimation Page 1.png
 
Introduction to Maximum Likelihood Estimation Page 2.png

 

Introduction to Maximum Likelihood Estimation Page 3.png

Introduction to Maximum Likelihood Estimation Page 4.png
Introduction to Maximum Likelihood Estimation Page 5.png
Introduction to Maximum Likelihood Estimation Page 6.png
Introduction to Maximum Likelihood Estimation Page 7.png
Introduction to Maximum Likelihood Estimation Page 8.png

 

References

www.cscu.cornell.edu/news/statnews/stnews50.pdf

en.wikipedia.org/wiki/Maximum_likelihood

en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm

statgen.iop.kcl.ac.uk/bgim/mle/sslike_1.html

eniac.cs.qc.cuny.edu/andrew/gcml-11/lecture10c.pptx

statweb.stanford.edu/~susan/courses/s200/lectures/lect11.pdf


Retrieved from "https://www.projectrhea.org/rhea/index.php?title=MLEforGMM&oldid=64612"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

Basic linear algebra uncovers and clarifies very important geometry and algebra.

Dr. Paul Garrett