| Line 53: | Line 53: | ||
<br> | <br> | ||
As you can see, the time to calculate the solution becomes longer and longer. So linear time is about the fastest way to compute an answer where polynomial time is very manageable for the time a computer needs to process a problem. | As you can see, the time to calculate the solution becomes longer and longer. So linear time is about the fastest way to compute an answer where polynomial time is very manageable for the time a computer needs to process a problem. | ||
| + | |||
| + | <h2><center>What is the difference between P and NP?</center></h2> | ||
| + | <hr> | ||
| + | <br> | ||
| + | P stands for “polynomial time”. This the subset of problems that can be guaranteed to be solved in a polynomial amount of time related to their input length. Problems in P commonly operate on single inputs, lists, or matrices, and can occasionally apply to graphs. The typical types of operations they perform are mathematical operators, sorting, finding minimum and maximum values, determinates, and many others. | ||
| + | <br> | ||
| + | Some examples of problems in P are: | ||
| + | <br> | ||
| + | {| border="1" class="wikitable" | ||
| + | |- | ||
| + | ! Name | ||
| + | ! Complexity | ||
| + | ! Description | ||
| + | |- | ||
| + | | Array Indexing | ||
| + | | O(1) | ||
| + | | Selecting an element in an array | ||
| + | |- | ||
| + | | Binary Search | ||
| + | | O(log(n)) | ||
| + | | Searching through a sorted list of values by starting in the middle and eliminating half of the remaining values at each iteration. | ||
| + | |} | ||
| + | <br> | ||
| + | |||
<center><h2>In A World Where P=NP</h2></center> | <center><h2>In A World Where P=NP</h2></center> | ||
<hr> | <hr> | ||
<br> | <br> | ||
| + | |||
A theoretical computer mathematician makes THE breakthrough. At first he is overjoyed at his success. | A theoretical computer mathematician makes THE breakthrough. At first he is overjoyed at his success. | ||
Revision as of 10:48, 27 April 2014
What is a "polynomial time algorithm", and what isn't? Is there a difference? What do we know about these two concepts?
Contents
- 1 What is this P vs NP?
- 1.1 You may have heard about a problem called the P vs NP Problem. It's a problem that falls under both Computer Science and Mathematics, particularly a field called Theoretical Computer Science. The subject is part of Computational Complexity Theory. It's practically the study of computing and consequently its resources (such as time it takes to compute, the space/RAM, and power consumption). If I haven't made out how big of a deal this problem is; beginning 2000, there are seven major math problems selected by the Clay Mathematics Institute which are called the Millennium Problems. Well, it so happens that this P vs NP problem is one of those seven major math problems and the first solution to the P vs NP problem is a guaranteed US $1,000,0000 from the Clay Mathematics Institute. Oh and did I mention that only ONE problem has been solved so far... But I still haven't answered the question: WHAT IS P VS. NP? . . . SO LET'S DIVE IN . . . Time Complexity
- 1.2 What is the difference between P and NP?
- 1.3 In A World Where P=NP
What is this P vs NP?
You may have heard about a problem called the P vs NP Problem. It's a problem that falls under both Computer Science and Mathematics, particularly
a field called Theoretical Computer Science.
The subject is part of Computational Complexity Theory. It's practically the study of computing and consequently its resources (such as time it takes to compute, the space/RAM, and power consumption).
If I haven't made out how big of a deal this problem is; beginning 2000, there are seven major math problems selected by the Clay Mathematics Institute which are called the Millennium Problems.
Well, it so happens that this P vs NP problem is one of those seven major math problems and the first solution to the P vs NP problem is a guaranteed US $1,000,0000 from the Clay Mathematics Institute.
Oh and did I mention that only ONE problem has been solved so far...
But I still haven't answered the question: WHAT IS P VS. NP?
.
.
.
SO LET'S DIVE IN
.
.
.
Time Complexity
We begin with time complexity.
Time complexity is basically the amount of time that an algorithm needs to run to give a final output or solution.
So let's take a large number and run through each number. So for example, 1,000,000,000,000 would take 12 steps to get through. The time to do this is denoted by a big O and in this case, the big O is followed by a one: O(1) to represent that it is a constant time problem.
Next let us take two large numbers; let's say the number 1,000,000 where there's 7 digits which we denote with n=7 (which we'll call the sample size) and the number 2,000,000 with n=7.
We add them:
1,000,000
+2,000,000
3,000,000
That is considered Linear time denoted by O(n).
Now let's multiply two numbers: 23 with n=2 and 37 with n=2
We multiply: 23
37
161
+690
851
This is consider Polynomial time denoted in this instance O($ n^2 $). In general polynomial time is denoted O($ n^k $) where k>1.
We can continue down with complexity and larger times. The graphs below demonstrates different computational time steps.
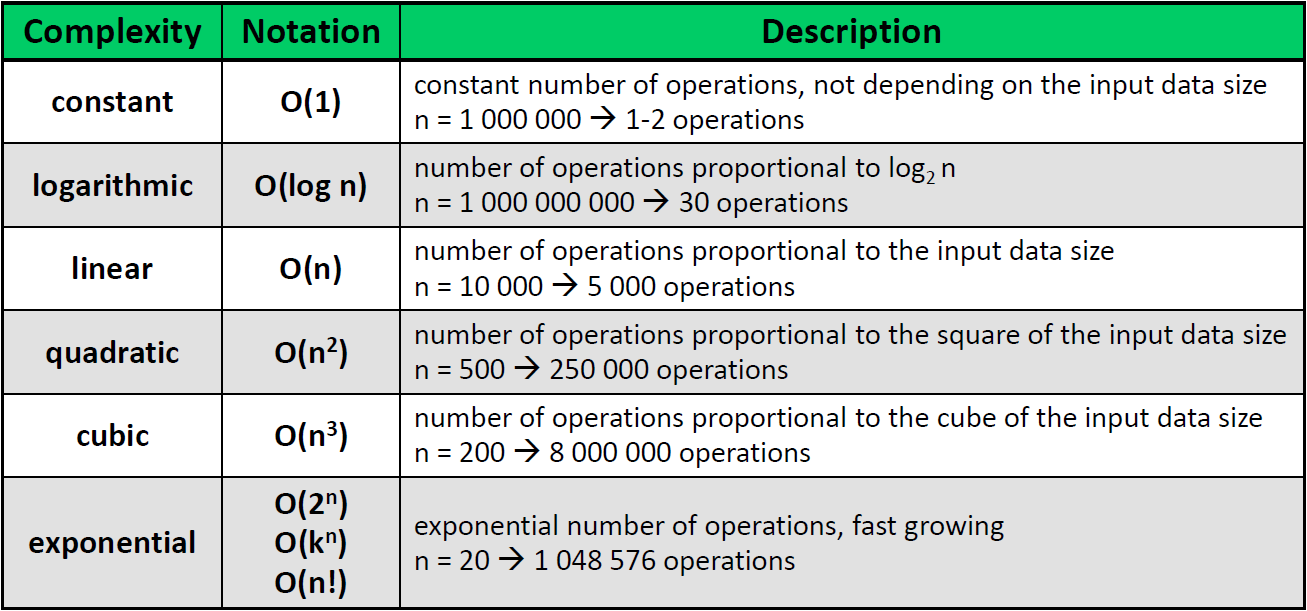
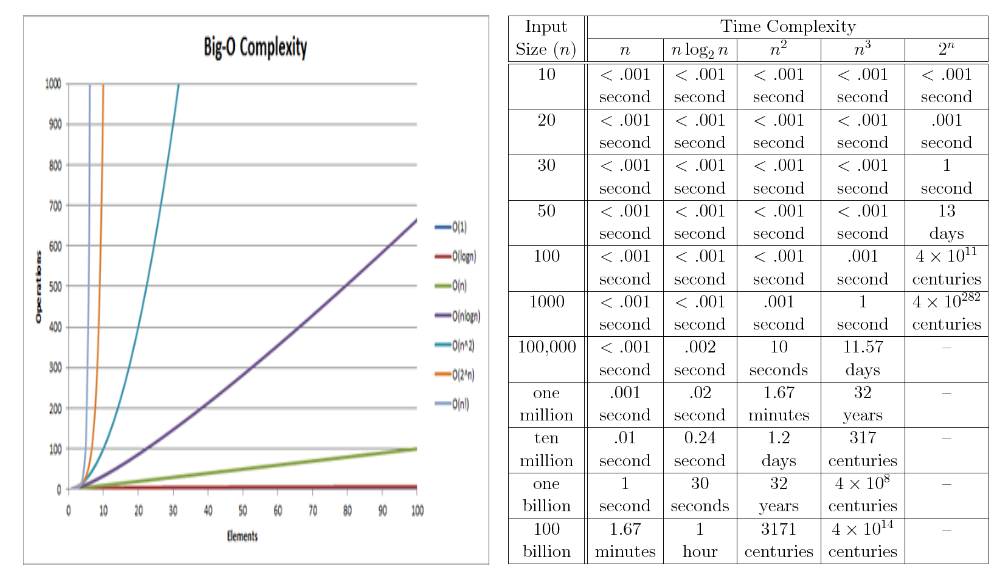
As you can see, the time to calculate the solution becomes longer and longer. So linear time is about the fastest way to compute an answer where polynomial time is very manageable for the time a computer needs to process a problem.
What is the difference between P and NP?
P stands for “polynomial time”. This the subset of problems that can be guaranteed to be solved in a polynomial amount of time related to their input length. Problems in P commonly operate on single inputs, lists, or matrices, and can occasionally apply to graphs. The typical types of operations they perform are mathematical operators, sorting, finding minimum and maximum values, determinates, and many others.
Some examples of problems in P are:
Name
Complexity
Description
Array Indexing
O(1)
Selecting an element in an array
Binary Search
O(log(n))
Searching through a sorted list of values by starting in the middle and eliminating half of the remaining values at each iteration.
In A World Where P=NP
A theoretical computer mathematician makes THE breakthrough. At first he is overjoyed at his success.
He tests it on the factorization problem and he breaks apart a billion sized number into its factors in mere minutes that would have taken centuries of supercomputer power to solve.
After the excitement wears off, the stark reality of what he now has sinks in.
In his hands lies the key to most of data encryption, the solution to many of scientific problems, optimization of routes such as for market strategies and lest we forget, a $1,000,000 prize from Clay Institute.
Like any human, curiosity gets the best of him and he wanted to test out the full power of his solution. He goes to Wallstreet and in the middle of the a major trade, he easily hacks right through the RSA encryption security and transfers some of the money to a bank account in Switzerland he previously just set up.
He instantly regrets his action, fearing legal reprecutions but none come. Plagued with guilt, we makes good of his stolen money and opens a scientific oriented company to solve major problems in biochemistry, physics, and economics.
Here's problems he manages to solve that
- Biochemistry: Protein and enzyme folding for cures
- Physics: the many body problem and chaotic systems
- Economics: Ideal routes to save on time and gas
Check-Out the Travelling Salesman 2012 Movie Info: http://www.imdb.com/title/tt1801123/
.
.
.
SO LET'S DIVE IN
.
.
.
Time Complexity
We begin with time complexity.
Time complexity is basically the amount of time that an algorithm needs to run to give a final output or solution.
So let's take a large number and run through each number. So for example, 1,000,000,000,000 would take 12 steps to get through. The time to do this is denoted by a big O and in this case, the big O is followed by a one: O(1) to represent that it is a constant time problem.
Next let us take two large numbers; let's say the number 1,000,000 where there's 7 digits which we denote with n=7 (which we'll call the sample size) and the number 2,000,000 with n=7.
We add them:
+2,000,000
3,000,000
That is considered Linear time denoted by O(n).
Now let's multiply two numbers: 23 with n=2 and 37 with n=2
We multiply:37
161
+690
851
This is consider Polynomial time denoted in this instance O($ n^2 $). In general polynomial time is denoted O($ n^k $) where k>1.
We can continue down with complexity and larger times. The graphs below demonstrates different computational time steps.


As you can see, the time to calculate the solution becomes longer and longer. So linear time is about the fastest way to compute an answer where polynomial time is very manageable for the time a computer needs to process a problem.
What is the difference between P and NP?
P stands for “polynomial time”. This the subset of problems that can be guaranteed to be solved in a polynomial amount of time related to their input length. Problems in P commonly operate on single inputs, lists, or matrices, and can occasionally apply to graphs. The typical types of operations they perform are mathematical operators, sorting, finding minimum and maximum values, determinates, and many others.
Some examples of problems in P are:
| Name | Complexity | Description |
|---|---|---|
| Array Indexing | O(1) | Selecting an element in an array |
| Binary Search | O(log(n)) | Searching through a sorted list of values by starting in the middle and eliminating half of the remaining values at each iteration. |
In A World Where P=NP
A theoretical computer mathematician makes THE breakthrough. At first he is overjoyed at his success.
He tests it on the factorization problem and he breaks apart a billion sized number into its factors in mere minutes that would have taken centuries of supercomputer power to solve.
After the excitement wears off, the stark reality of what he now has sinks in.
In his hands lies the key to most of data encryption, the solution to many of scientific problems, optimization of routes such as for market strategies and lest we forget, a $1,000,000 prize from Clay Institute.
Like any human, curiosity gets the best of him and he wanted to test out the full power of his solution. He goes to Wallstreet and in the middle of the a major trade, he easily hacks right through the RSA encryption security and transfers some of the money to a bank account in Switzerland he previously just set up.
He instantly regrets his action, fearing legal reprecutions but none come. Plagued with guilt, we makes good of his stolen money and opens a scientific oriented company to solve major problems in biochemistry, physics, and economics.
- Biochemistry: Protein and enzyme folding for cures
- Physics: the many body problem and chaotic systems
- Economics: Ideal routes to save on time and gas
Check-Out the Travelling Salesman 2012 Movie Info: http://www.imdb.com/title/tt1801123/

