| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | What is a Markov chain/process? What can you do with it? And why are people talking about them? | + | What is a Markov chain/process? What can you do with it? And why are people talking about them? <br>[[2014 Spring MA 375 Walther|Back to MA375 Spring 2014]] <br> Tianyi Zhang: zhan1035@purdue.edu ;<br> Sui Fang: fang52@purdue.edu ; <br> Christopher Peralta: cperalta@purdue.edu;<br> Lei Zhong: zhong9@purdue.edu ;<br> Nathan Accornero: naccorne@purdue.edu<br> <br> |
| − | <br>[[2014 Spring MA 375 Walther|Back to MA375 Spring 2014]] | + | |
| − | <br> | + | |
| − | Tianyi Zhang: zhan1035@purdue.edu ;<br> Sui Fang: fang52@purdue.edu ; <br> Christopher Peralta: cperalta@purdue.edu;<br> Lei Zhong: zhong9@purdue.edu ;<br> Nathan Accornero: naccorne@purdue.edu<br> | + | |
| − | <br> | + | |
| − | Outline of the Project:<br>A) What is a Markov Chain? <br>-Stochastic process<br>-Definition of Markov Chain<br>-Concrete examples and several properties<br>B) What can we do with it?<br> -Transition Probabilities and Transition Matrix<br> -Computation with Transition Matrix<br> -Matrix limits and Markov Chains<br>C) Why is a Markov Chain useful?<br> -Applications in Real Life with examples and computation (simple weather prediction model) <br>- Markov Chain and PageRank | + | Outline of the Project:<br>A) What is a Markov Chain? <br>-Stochastic process<br>-Definition of Markov Chain<br>-Concrete examples and several properties<br>B) What can we do with it?<br> -Transition Probabilities and Transition Matrix<br> -Computation with Transition Matrix<br> -Matrix limits and Markov Chains<br>C) Why is a Markov Chain useful?<br> -Applications in Real Life with examples and computation (simple weather prediction model) <br>- Markov Chain and PageRank |
| − | <br>1.What is a Markov chain?<br>To answer this question, we need to know the definition of a stochastic process, because a Markov Chain is a special type of stochastic process. | + | <br>1.What is a Markov chain?<br>To answer this question, we need to know the definition of a stochastic process, because a Markov Chain is a special type of stochastic process.
A stochastic process { X(t), t∈T } is an ordered collection of random variables, T where T is the index set and if t is a time in the set, X(t) is the process’s state (represented by a numerical value) at time t. |
Explanation: We may think X1, X2,…,Xn as samples of an experiment. In a stochastic process, they represent the states of a process. Clearly, X1 is called the initial state and Xn represents the state at time n. In introductory probability courses, we are familiar with models that use X1,…,Xn as independently identically distributed (iid) random variables. However, note that states do not necessarily have to be independently identically distributed. This note is especially important to eliminate confusion for first time learners of Markov Chains. | Explanation: We may think X1, X2,…,Xn as samples of an experiment. In a stochastic process, they represent the states of a process. Clearly, X1 is called the initial state and Xn represents the state at time n. In introductory probability courses, we are familiar with models that use X1,…,Xn as independently identically distributed (iid) random variables. However, note that states do not necessarily have to be independently identically distributed. This note is especially important to eliminate confusion for first time learners of Markov Chains. | ||
| Line 13: | Line 9: | ||
<br> | <br> | ||
| − | Definition of a Markov Chain: | + | |
| + | |||
| + | Definition of a Markov Chain: A Markov Chain is a special case of stochastic processes that must hold a few important assumptions. The first of which is the Markov Assumption: A discrete stochastic process is a Markov Chain if and only if P(Xn = jn| Xn-1=jn-1 , Xn-2=jn-2 , … , X0 = j0) = P(Xn = jn | Xn-1 = jn-1). In other words, the current state of the process is the only thing that affects its immediate future state. Therefore, all previous states are ignored and irrelevant. This trait is often referred to as the memoryless property. The second important assumption is stationarity: A Markov Chain is stationary if and only if P(Xn = j | Xn-1 = i) = P(Xm = j | Xm-1 = i). In other words, the probability of a transition from state i to j will be constant over any time period throughout the process. | ||
| + | |||
| + | |||
| + | |||
| + | A Markov Chain can be modeled as either discrete or continuous processes. For a discrete process, it follows uniform time steps where the process is in a certain state for the entire time period. In this case, we refer to the discrete time periods as epochs. For example, each epoch could represent a day and the process must be in a single state for the entire day and transition to another state the next day. A continuous Markov chain closely resembles a discrete one, however the transitions are no longer represented by probabilities. Transitions are now represented with the rates at which a process changes from state i to state j (where the rate λ is the number of transitions per given time period). <br> | ||
<br> | <br> | ||
| − | A concrete example:<br>Lets consider a person that has two choices of drinks for his breakfast every morning, milk or coffee. We let Xi=1 if the person chooses to drink milk on the i'th morning. Let Xi=2 if the person chooses to drink coffee on the i'th morning. In this case, the sequence of cases (random variables) X1, X2,…,xn is a stochastic process with two possible states at each time. To make it a Markov chain, consider that most people will usually switch rather than drink the same thing every day, and our person prefers milk more than coffee. Thus assume probability of that person choosing milk today given he chose milk yesterday is 0.3. The probability that he chooses coffee given he chose coffee yesterday is 0.2. Then this sequence of states becomes a Markov Chain. <br><br> <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 1 | ''X''<sub>''n''</sub> = 1) = 0.3</span>, <span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 2 | ''X''<sub>''n''</sub> = 1) = 1 − 0.3 = 0.7</span><br> <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 1 | ''X''<sub>''n''</sub> = 2) = 1 − 0.2 = 0.8</span>, <span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 2 | ''X''<sub>''n''</sub> = 2) = 0.2</span><br> <br>[[Image:Milk and Coffee.PNG]] | + | A concrete example:<br>Lets consider a person that has two choices of drinks for his breakfast every morning, milk or coffee. We let Xi=1 if the person chooses to drink milk on the i'th morning. Let Xi=2 if the person chooses to drink coffee on the i'th morning. In this case, the sequence of cases (random variables) X1, X2,…,xn is a stochastic process with two possible states at each time. To make it a Markov chain, consider that most people will usually switch rather than drink the same thing every day, and our person prefers milk more than coffee. Thus assume probability of that person choosing milk today given he chose milk yesterday is 0.3. The probability that he chooses coffee given he chose coffee yesterday is 0.2. Then this sequence of states becomes a Markov Chain. <br><br> <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 1 | ''X''<sub>''n''</sub> = 1) = 0.3</span>, <span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 2 | ''X''<sub>''n''</sub> = 1) = 1 − 0.3 = 0.7</span><br> <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 1 | ''X''<sub>''n''</sub> = 2) = 1 − 0.2 = 0.8</span>, <span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = 2 | ''X''<sub>''n''</sub> = 2) = 0.2</span><br> <br>[[Image:Milk and Coffee.PNG]] <br> <br>As you can see from the diagram, if the person drinks milk today there is a 30% chance he will drink it again tomorrow and there is a 70% chance he will drink coffee tomorrow. <br> |
| − | <br> | + | |
| − | <br>As you can see from the diagram, if the person | + | |
| − | <br> | + | |
| − | What can we do with this?<br> Transition probabilities and Transition Matrix<br>We define Pij to be the probability that the future state is j given the present state is i.<br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''j'' | ''X''<sub>''n''</sub> = ''i'') = ''P''<sub>''i''''j | + | What can we do with this?<br> Transition probabilities and Transition Matrix<br>We define Pij to be the probability that the future state is j given the present state is i.<br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''j'' | ''X''<sub>''n''</sub> = ''i'') = ''P''<sub>''i''''j''</sub></span><br>They are called transition distributions. If a Markov Chain’s transition distributions do not depend on n (just like the above example), then we can say the Markov Chain has stationary transition distributions.<br>In particular, a Markov Chain with stationary transition distributions can be represented by a Transition Matrix. For instance, the transition Matrix for the above Example is:<br> <br><math>\begin{pmatrix} |
0.3 & 0.7 \\ | 0.3 & 0.7 \\ | ||
0.8 & 0.2 | 0.8 & 0.2 | ||
| − | \end{pmatrix}</math> <br> <br> | + | \end{pmatrix}</math> <br> <br> <br>More Generally:<math>P=\begin{bmatrix} |
| − | <br>More Generally:<math>P=\begin{bmatrix} | + | |
P_{11} & \cdots & P_{1k} \\ | P_{11} & \cdots & P_{1k} \\ | ||
\vdots & \ddots & \vdots \\ | \vdots & \ddots & \vdots \\ | ||
P_{k1} & \cdots & P_{kk} | P_{k1} & \cdots & P_{kk} | ||
| − | \end{bmatrix}</math> | + | \end{bmatrix}</math> <br>General Rule for nth state distribution:<span class="texhtml">''x''<sub>''n''</sub> = ''x''<sub>''n'' − 1</sub>''P''</span> |
| − | <br>General Rule for nth state distribution:< | + | |
| − | <br>'''Important Notes''':<br>< | + | <br>'''Important Notes''':<br><span class="texhtml">''P''<sub>''i''''j''</sub></span> in the above matrix represents <span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''j'' | ''X''<sub>''n''</sub> = ''i'')</span>, it turns out that the the sum of the entries in each row is 1 (This follows the same notation as my probability textbook and most of the professional articles I have found with online libraries). However, in some textbooks (for example, my linear algebra textbook) and resources I have found on the Internet, <span class="texhtml">''P''<sub>''i''''j''</sub></span> in the Matrix = <span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''i'' | ''X''<sub>''n''</sub> = ''j'')</span>, this means the sum of every entry in each column is 1. To avoid confusion, we are going to follow the first notation style in this note. <br><br>The transition matrix makes computations in a Markov Chain much easier. In the breakfast example above (stationary transition probability), if we are given that a person drinks milk at time n,<span class="texhtml">''X''<sub>''n''</sub> = 1</span>, we can determine the probability distribution of <span class="texhtml">''X''<sub>''n'' + 3</sub></span>. The initial state distribution can be written as a row vector : <math>\begin{pmatrix}1 & 0\end{pmatrix}</math> <br><math>x_{n+3}=x_{n+2}P=(x_{n+1}P)P=((x_nP)P)P=x_nP^3=\begin{pmatrix}1 & 0\end{pmatrix} |
| − | <br><br>The transition matrix makes computations in a Markov Chain much easier. In the breakfast example above (stationary transition probability), if we are given that a person drinks milk at time n,< | + | |
| − | <br><math>x_{n+3}=x_{n+2}P=(x_{n+1}P)P=((x_nP)P)P=x_nP^3=\begin{pmatrix}1 & 0\end{pmatrix} | + | |
\begin{pmatrix} | \begin{pmatrix} | ||
0.3 & 0.7 \\ | 0.3 & 0.7 \\ | ||
0.8 & 0.2 | 0.8 & 0.2 | ||
| − | \end{pmatrix}^3</math> | + | \end{pmatrix}^3</math> <br><math>x_{n+3}=\begin{pmatrix}0.475 & 0.525\end{pmatrix}</math> <br>This means given the person drinks milk today, three days later, there is a 47.5% chance he will drink milk and a 52.5% he will drink coffee. <br><br>- Matrix Limits and Markov Chains <br>In the Linear Algebra courses (MA351 and MA353 at Purdue University), we learn that a diagonalizable Matrix A can be represented in the form <span class="texhtml">''A'' = ''Q''''D''''Q''<sup> − 1</sup></span>. <br>Where <math>D=\begin{bmatrix} |
| − | <br><math>x_{n+3}=\begin{pmatrix}0.475 & 0.525\end{pmatrix}</math> | + | |
| − | <br>This means given the person drinks milk today, three days later, there is a 47.5% chance he will drink milk and a 52.5% he will drink coffee. | + | |
| − | <br><br>- Matrix Limits and Markov Chains | + | |
| − | <br>In the Linear Algebra courses (MA351 and MA353 at Purdue University), we learn that a diagonalizable Matrix A can be represented in the form < | + | |
| − | <br>Where <math>D=\begin{bmatrix} | + | |
r_{1} & \cdots & 0 \\ | r_{1} & \cdots & 0 \\ | ||
\vdots & \ddots & \vdots \\ | \vdots & \ddots & \vdots \\ | ||
0 & \cdots & r_n | 0 & \cdots & r_n | ||
| − | \end{bmatrix}</math>, where < | + | \end{bmatrix}</math>, where <span class="texhtml">''r''<sub>1</sub>...''r''<sub>''n''</sub></span> are eigenvalues of the matrix A, and Q are has columns corresponding to the eigenvectors. <br><math>A^n=QDQ^{-1}QDQ^{-1}...QDQ^{-1}=QD^nQ^{-1}; |
| − | <br><math>A^n=QDQ^{-1}QDQ^{-1}...QDQ^{-1}=QD^nQ^{-1}; | + | \lim_{n \to \infty}A^n=\lim_{n \to \infty}(QD^nQ^{-1})</math>. <br>Since D is a diagonal matrix, it’s very easy to compute its powers. In the breakfast example above, we are able to compute the matrix limits. <br><math>P=\begin{pmatrix} |
| − | \lim_{n \to \infty}A^n=\lim_{n \to \infty}(QD^nQ^{-1})</math>. | + | |
| − | <br>Since D is a diagonal matrix, it’s very easy to compute its powers. In the breakfast example above, we are able to compute the matrix limits. | + | |
| − | <br><math>P=\begin{pmatrix} | + | |
0.3 & 0.7 \\ | 0.3 & 0.7 \\ | ||
0.8 & 0.2 | 0.8 & 0.2 | ||
| − | \end{pmatrix}</math>; | + | \end{pmatrix}</math>; <br>The Characteristic Polynomial for P is: <br><math>(0.3-r)(0.2-r)-0.8*0.7=0; |
| − | <br>The Characteristic Polynomial for P is: | + | |
| − | <br><math>(0.3-r)(0.2-r)-0.8*0.7=0; | + | |
r_1=1; r_2=-0.5; | r_1=1; r_2=-0.5; | ||
Thus,D=\begin{pmatrix} | Thus,D=\begin{pmatrix} | ||
1 & 0 \\ | 1 & 0 \\ | ||
0 & -0.5 | 0 & -0.5 | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math> <br>Solving the linear systems, eigenvectors for P are: <br><math>\begin{pmatrix} |
| − | <br>Solving the linear systems, eigenvectors for P are: | + | |
| − | <br><math>\begin{pmatrix} | + | |
1 \\ | 1 \\ | ||
1 | 1 | ||
| Line 74: | Line 57: | ||
1 & 7 \\ | 1 & 7 \\ | ||
1 & -8 | 1 & -8 | ||
| − | \end{pmatrix}</math>; | + | \end{pmatrix}</math>; <br><math>\lim_{n \to \infty}P^n=\lim_{n \to \infty}(QD^nQ^{-1})=\lim_{n \to \infty}\begin{pmatrix} |
| − | <br><math>\lim_{n \to \infty}P^n=\lim_{n \to \infty}(QD^nQ^{-1})=\lim_{n \to \infty}\begin{pmatrix} | + | |
1 & 7 \\ | 1 & 7 \\ | ||
1 & -8 | 1 & -8 | ||
| Line 86: | Line 68: | ||
1 & 7 \\ | 1 & 7 \\ | ||
1 & -8 | 1 & -8 | ||
| − | \end{pmatrix}^{-1}</math> | + | \end{pmatrix}^{-1}</math> <br><math>=\lim_{n \to \infty}\begin{pmatrix} |
| − | <br><math>=\lim_{n \to \infty}\begin{pmatrix} | + | |
(8+7(-0.5)^n)/15 & 7/15 \\ | (8+7(-0.5)^n)/15 & 7/15 \\ | ||
(8-8(-0.5)^n)/15 &(7-8(-0.5)^n)/15 | (8-8(-0.5)^n)/15 &(7-8(-0.5)^n)/15 | ||
| Line 94: | Line 75: | ||
8/15 & 7/15 \\ | 8/15 & 7/15 \\ | ||
8/15 & 7/15 | 8/15 & 7/15 | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math> <br>We put the initial condition into the equation: <br><math>\begin{pmatrix} |
| − | <br>We put the initial condition into the equation: | + | |
| − | <br><math>\begin{pmatrix} | + | |
1 & 0 | 1 & 0 | ||
\end{pmatrix}\begin{pmatrix} | \end{pmatrix}\begin{pmatrix} | ||
| Line 103: | Line 82: | ||
\end{pmatrix}=\begin{pmatrix} | \end{pmatrix}=\begin{pmatrix} | ||
8/15 & 7/15 | 8/15 & 7/15 | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math> <br>In fact, we will always get <math>\begin{pmatrix} |
| − | <br>In fact, we will always get <math>\begin{pmatrix} | + | |
8/15 & 7/15 | 8/15 & 7/15 | ||
| − | \end{pmatrix}</math> whether he drinks milk or coffee on the first day. This indicates that over a long time period, he will drink milk in 8/15 of days, and drink coffee in 7/15 of days. | + | \end{pmatrix}</math> whether he drinks milk or coffee on the first day. This indicates that over a long time period, he will drink milk in 8/15 of days, and drink coffee in 7/15 of days. <br><br>Use MatLab to verify our result, just use n=1000: <br>[[Image:Matlab 1.PNG]] <br><br><br>3. Why are people talking about Markov Chains? <br>- Applications of Markov Chains in Science and Real Life <br>Markov Chains have lots of applications in scientific research, because many things can be modeled using Markov Chains. In economics and finance, Markov Chains can help investors predict the volatility of asset returns. In biology, Markov chains can be used in population genetics research. In the simplest cases, Markov chains can be used in weather predictions. <br><br>We now construct a very simple sample case of weather prediction. Assume a city's weather has 3 distinct states: Sunny, Rainy and Overcast. These states, respectively, have the following sample space S= {0,1,2}. Suppose that the probability distribution of the next day only depends on the weather state of today (This is relatively reasonable in real cases), and given that: <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''S''''u''''n''''n''''y'' | ''X''<sub>''n''</sub> = ''S''''u''''n''''n''''y'') = 0.5</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''R''''a''''i''''n''''y'' | ''X''<sub>''n''</sub> = ''S''''u''''n''''n''''y'') = 0.2</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''O''''v''''e''''r''''c''''a''''s''''t'' | ''X''<sub>''n''</sub> = ''S''''u''''n''''n''''y'') = 1 − 0.5 − 0.2 = 0.3</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''S''''u''''n''''n''''y'' | ''X''<sub>''n''</sub> = ''R''''a''''i''''n''''y'') = 0.6</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''R''''a''''i''''n''''y'' | ''X''<sub>''n''</sub> = ''R''''a''''i''''n''''y'') = 0.3</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''O''''v''''e''''r''''c''''a''''s''''t'' | ''X''<sub>''n''</sub> = ''R''''a''''i''''n''''y'') = 1 − 0.6 − 0.3 = 0.1</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''S''''u''''n''''n''''y'' | ''X''<sub>''n''</sub> = ''O''''v''''e''''r''''c''''a''''s''''t'') = 0.2</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''R''''a''''i''''n''''y'' | ''X''<sub>''n''</sub> = ''O''''v''''e''''r''''c''''a''''s''''t'') = 0.6</span>; <br><span class="texhtml">''P''(''X''<sub>''n'' + 1</sub> = ''O''''v''''e''''r''''c''''a''''s''''t'' | ''X''<sub>''n''</sub> = ''O''''v''''e''''r''''c''''a''''s''''t'') = 1 − 0.2 − 0.6 = 0.2</span>; <br>[[Image:Weather.PNG]] <br><br>Transition Matrix P for this Model: <br><math>\begin{pmatrix} |
| − | <br><br>Use MatLab to verify our result, just use n=1000: | + | |
| − | <br>[[Image: | + | |
| − | <br><br><br>3. Why are people talking about Markov Chains? | + | |
| − | <br>- Applications of Markov Chains in Science and Real Life | + | |
| − | <br>Markov Chains have lots of applications in scientific research, because many things can be modeled using Markov Chains. In economics and finance, Markov Chains can help investors predict the volatility of asset returns. In biology, Markov chains can be used in population genetics research. In the simplest cases, Markov chains can be used in weather predictions. | + | |
| − | <br><br>We now construct a very simple sample case of weather prediction. Assume a city's weather has 3 distinct states: Sunny, Rainy and Overcast. These states, respectively, have the following sample space S= {0,1,2}. Suppose that the probability distribution of the next day only depends on the weather state of today (This is relatively reasonable in real cases), and given that: | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>< | + | |
| − | <br>[[Image:Weather.PNG]] | + | |
| − | <br><br>Transition Matrix P for this Model: | + | |
| − | <br><math>\begin{pmatrix} | + | |
0.5 & 0.2 & 0.3 \\ | 0.5 & 0.2 & 0.3 \\ | ||
0.6 & 0.3 & 0.1 \\ | 0.6 & 0.3 & 0.1 \\ | ||
0.2 & 0.6 & 0.2 \\ | 0.2 & 0.6 & 0.2 \\ | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math> <br><br>Suppose we know the weather is overcast on Monday (Today), then we can determine the probability distribution of weather over the next several days (weather forecasting). For instance, on Wednesday: <br><math>x_{n+2}=x_{n}P^2=\begin{pmatrix} |
| − | <br><br>Suppose we know the weather is overcast on Monday (Today), then we can determine the probability distribution of weather over the next several days (weather forecasting). For instance, on Wednesday: | + | |
| − | <br><math>x_{n+2}=x_{n}P^2=\begin{pmatrix} | + | |
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{pmatrix} | \end{pmatrix} | ||
| Line 145: | Line 103: | ||
=\begin{pmatrix} | =\begin{pmatrix} | ||
0.5 & 0.34 & 0.16 | 0.5 & 0.34 & 0.16 | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math> <br>This means on Wednesday, the probability is 0.5 for sunny, 0.34 for rainy and 0.16 for overcast given that Monday is overcast. <br><br>We can also use matrix limits to determine the long-term probability following the procedure in Part II. Since it’s little bit complicated to diagonalize a 3*3 matrix by hand, especially for a matrix with complex eigenvalues and eigenvectors, we use Matlab instead: <br>[[Image:Matlab 2.PNG]] <br><math>\lim_{n \to \infty}P^n=\lim_{n \to \infty}(QD^nQ^{-1})=\begin{pmatrix} |
| − | <br>This means on Wednesday, the probability is 0.5 for sunny, 0.34 for rainy and 0.16 for overcast given that Monday is overcast. | + | |
| − | <br><br>We can also use matrix limits to determine the long-term probability following the procedure in Part II. Since it’s little bit complicated to diagonalize a 3*3 matrix by hand, especially for a matrix with complex eigenvalues and eigenvectors, we use Matlab instead: | + | |
| − | <br>[[Image: | + | |
| − | <br><math>\lim_{n \to \infty}P^n=\lim_{n \to \infty}(QD^nQ^{-1})=\begin{pmatrix} | + | |
50/107 & 34/107 & 23/107 \\ | 50/107 & 34/107 & 23/107 \\ | ||
50/107 & 34/107 & 23/107 \\ | 50/107 & 34/107 & 23/107 \\ | ||
50/107 & 34/107 & 23/107 \\ | 50/107 & 34/107 & 23/107 \\ | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math> <br><br>Therefore, for a single day randomly picked from the calendar, this city has a probability of 50/107 of sunny weather, 34/107 for rainy weather and 23/107 for overcast weather. Verify this result with Matlab, take n=10000: <br>[[Image:Matlab 3.PNG]] |
| − | <br><br>Therefore, for a single day randomly picked from the calendar, this city has a probability of 50/107 of sunny weather, 34/107 for rainy weather and 23/107 for overcast weather. | + | |
| − | Verify this result with Matlab, take n=10000: | + | |
| − | <br>[[Image: | + | |
| + | <br> <br>Application in PageRank <br>[[Image:PageRank 1.png]] <br><br>One of the significant application involving Markov chains is PageRank. As demonstrated in the picture, it is a simulation of the Probability that surfer will visit each webpage at time t. Actually, the process is more complicated. To simplify it, we just consider the basic idea of Markov Chain, we assume that for each step, the surfer can either follow the links on the current website or jump randomly to another website in the network(the number of website is constant n). Namely, with probability P, the surfer will follow the link on the current website, and with chance of (1-P), he will jump to websites which have no link on the current website. | ||
| − | <br> | + | <br>In order to have a glimpse of how it works. We attach the codes of our team member's CS class as follows. <br>Suppose P = 0.75 and n = 5 <br>web1 has link on web4, <br>web2 has link on web1, <br>web3 has link on web1, <br>web4 has links on web2, web3 and web5, <br>web5 has link on web3 |
| − | <br> | + | |
| − | <br><br> | + | |
| − | <br> | + | <br> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <br>numsims = 5000; % Parameter controlling the number of simulations <br>G = [0 0 0 1 0; 1 0 0 0 0; 1 0 0 0 0; 0 1 1 0 1; 0 0 1 0 0]; <br>n = length(G); % size of network <br>state = 1; % initial state of the system <br>p = 0.75; % probability of following link on web page <br>M = zeros(n,n); % create the matrix of probabilities <br>for i = 1:n; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
for j = 1:n; | for j = 1:n; | ||
| − | + | M(i,j) = p*G(i,j)/sum(G(i,:)) + (1-p)/n; | |
| − | + | end | |
| − | end | + | |
| − | pages = zeros(1,n); | + | end |
| + | |||
| + | pages = zeros(1,n); % vector to hold number of times page visited | ||
| + | |||
| + | % Simulate a surfer's session for i=1:numsims | ||
| − | |||
| − | |||
prob = rand; | prob = rand; | ||
| − | + | if prob < M(state,1) | |
| − | + | state = 1; | |
| − | + | elseif prob < M(state,1) + M(state,2) | |
| − | + | state = 2; | |
| − | + | elseif prob < M(state,1) + M(state,2) + M(state,3) | |
| − | + | state = 3; | |
| − | + | elseif prob < M(state,1) + M(state,2) + M(state,3) + M(state,4) | |
| − | + | state = 4; | |
| − | + | else state = 5; | |
| − | + | end; | |
pages(state) = pages(state) + 1; | pages(state) = pages(state) + 1; | ||
if ~mod(i,numsims/5) | if ~mod(i,numsims/5) | ||
| − | + | fprintf('%6d %5.3f %5.3f %5.3f %5.3f %5.3f \n',i,pages/sum(pages)); | |
| − | + | end | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <br><br>The weather model and PageRank made by us are very simple examples of the real applications of Markov Chains. Many other models, such as prediction on genetic illness, also use Markov Chains. Yet they are too complex to show on this webpage. | + | end <br>[[Image:Matlab PageRank.png]] <br> <br> <br>If we increase the number of simulation to 500000, we can see a more stable pattern. <br>The results is <br> [[Image:Matlab PageRank 2.png]] <br> |
| − | + | ||
| − | <br><br>'''This project was originally conducted by Office Word, a link for the PDF file (already uploaded to this site) | + | |
| − | + | ||
| + | This shows an important concept within Markov Chains: steady-state probabilities. After a significant number of transitions, the process will fall into a general pattern and the initial state will no longer have an affect on the final state. Rather, each final state will be given a probability that is independent of the initial state. This can be clearly seen in the Page Rank code output above with the increasingly large number of transitions.<br> | ||
| + | |||
| + | Discussion: Even Markov Chain is great idea in this PageRank simulation example, there are still some challenge things we need to improve. First, the number of pages on the internet is not constant. Secondly, the links of on each webpage will change. Thirdly, the probability actually is really hard to be a constant. That is why we need other theories to improve our strategy, like Time Series and Stochastic Process.<br>The weather model and PageRank made by us are very simple examples of the real applications of Markov Chains. Many other models, such as prediction on genetic illness, also use Markov Chains. Yet they are too complex to show on this webpage. | ||
| + | |||
| + | |||
| + | |||
| + | In addition to the previous discrete applications of Markov Chain, continuous applications are just as important. Continuous Markov Chains are frequently used within queuing theory. Frequently service systems are modeled as a Markov Chain where the states are the number of customers in the system. Customer interarrival times are often modeled as an exponential variable where λ is the rate at which the number of customers (system state) increases by 1. Then the model can specify the number of servers and the various distributions of service times where a completed service will reduce the number of customers in the system by one. A Markov Chain model is very powerful because through using matrix calculations, one can extract very important properties of their modeled system crucial to decision making. A user will be able to determine average time that customers are in the system, time they are in the queue, and the average number of busy servers (just to name a few). From there, important decisions can be made regarding how to manage the modeled system such as how many servers to have (staffing decision) or how large to make a waiting room (queue size). | ||
| + | |||
| + | <br><br>'''This project was originally conducted by Office Word, a link for the PDF file (already uploaded to this site)''' can be found | ||
| + | |||
| + | Courses which group members have taken that are relevant to this project: IE336 (Operations Research – Stochastic Modeling), MA416(Probability), STAT417(Statistical Inference), MA 353 (Linear Algebra II), CS 314 (Numerical Methods), IE581(Simulation Design & Analysis). These courses have provided a large range of knowledge ranging from direct applications of Markov Chains to computing necessary matrix calculations important to Markov Chains. | ||
| + | |||
| + | <br> | ||
:[https://www.projectrhea.org/rhea/images/b/b5/MA375_project_Team5.pdf] | :[https://www.projectrhea.org/rhea/images/b/b5/MA375_project_Team5.pdf] | ||
| − | <br><br><br>References and Theorems & knowledge Sources: | + | |
| − | <br>- Morris H. Degroot, Mark J. Schervish, Probability and Statistics, 4th edition | + | <br><br><br>References and Theorems & knowledge Sources: <br>- Morris H. Degroot, Mark J. Schervish, Probability and Statistics, 4th edition <br>- Michael J. Evans, Jeffery S. Rosenthal, Probability and Statistics: The Science of Uncertainty, 2nd edition <br>- Stephen H. Friedberg, Arnold J. Insel, Linear Algebra, 4th edition <br>- Anne Greenbaum & Timothy P. Chartier, Numerical Methods, 1st edition |
| − | <br>- Michael J. Evans, Jeffery S. Rosenthal, Probability and Statistics: The Science of Uncertainty, 2nd edition | + | |
| − | <br>- Stephen H. Friedberg, Arnold J. Insel, Linear Algebra, 4th edition | + | |
| − | <br>- | + | |
| + | [[Markov Chains: what and how?:MA375Spring2014Walther]] | ||
| + | |||
[[Category:MA375Spring2014Walther]] [[Category:Math]] [[Category:Project]] | [[Category:MA375Spring2014Walther]] [[Category:Math]] [[Category:Project]] | ||
Latest revision as of 08:39, 23 April 2014
What is a Markov chain/process? What can you do with it? And why are people talking about them?
Back to MA375 Spring 2014
Tianyi Zhang: zhan1035@purdue.edu ;
Sui Fang: fang52@purdue.edu ;
Christopher Peralta: cperalta@purdue.edu;
Lei Zhong: zhong9@purdue.edu ;
Nathan Accornero: naccorne@purdue.edu
Outline of the Project:
A) What is a Markov Chain?
-Stochastic process
-Definition of Markov Chain
-Concrete examples and several properties
B) What can we do with it?
-Transition Probabilities and Transition Matrix
-Computation with Transition Matrix
-Matrix limits and Markov Chains
C) Why is a Markov Chain useful?
-Applications in Real Life with examples and computation (simple weather prediction model)
- Markov Chain and PageRank
1.What is a Markov chain?
To answer this question, we need to know the definition of a stochastic process, because a Markov Chain is a special type of stochastic process.
A stochastic process { X(t), t∈T } is an ordered collection of random variables, T where T is the index set and if t is a time in the set, X(t) is the process’s state (represented by a numerical value) at time t.
Explanation: We may think X1, X2,…,Xn as samples of an experiment. In a stochastic process, they represent the states of a process. Clearly, X1 is called the initial state and Xn represents the state at time n. In introductory probability courses, we are familiar with models that use X1,…,Xn as independently identically distributed (iid) random variables. However, note that states do not necessarily have to be independently identically distributed. This note is especially important to eliminate confusion for first time learners of Markov Chains.
Definition of a Markov Chain: A Markov Chain is a special case of stochastic processes that must hold a few important assumptions. The first of which is the Markov Assumption: A discrete stochastic process is a Markov Chain if and only if P(Xn = jn| Xn-1=jn-1 , Xn-2=jn-2 , … , X0 = j0) = P(Xn = jn | Xn-1 = jn-1). In other words, the current state of the process is the only thing that affects its immediate future state. Therefore, all previous states are ignored and irrelevant. This trait is often referred to as the memoryless property. The second important assumption is stationarity: A Markov Chain is stationary if and only if P(Xn = j | Xn-1 = i) = P(Xm = j | Xm-1 = i). In other words, the probability of a transition from state i to j will be constant over any time period throughout the process.
A Markov Chain can be modeled as either discrete or continuous processes. For a discrete process, it follows uniform time steps where the process is in a certain state for the entire time period. In this case, we refer to the discrete time periods as epochs. For example, each epoch could represent a day and the process must be in a single state for the entire day and transition to another state the next day. A continuous Markov chain closely resembles a discrete one, however the transitions are no longer represented by probabilities. Transitions are now represented with the rates at which a process changes from state i to state j (where the rate λ is the number of transitions per given time period).
A concrete example:
Lets consider a person that has two choices of drinks for his breakfast every morning, milk or coffee. We let Xi=1 if the person chooses to drink milk on the i'th morning. Let Xi=2 if the person chooses to drink coffee on the i'th morning. In this case, the sequence of cases (random variables) X1, X2,…,xn is a stochastic process with two possible states at each time. To make it a Markov chain, consider that most people will usually switch rather than drink the same thing every day, and our person prefers milk more than coffee. Thus assume probability of that person choosing milk today given he chose milk yesterday is 0.3. The probability that he chooses coffee given he chose coffee yesterday is 0.2. Then this sequence of states becomes a Markov Chain.
P(Xn + 1 = 1 | Xn = 1) = 0.3, P(Xn + 1 = 2 | Xn = 1) = 1 − 0.3 = 0.7
P(Xn + 1 = 1 | Xn = 2) = 1 − 0.2 = 0.8, P(Xn + 1 = 2 | Xn = 2) = 0.2
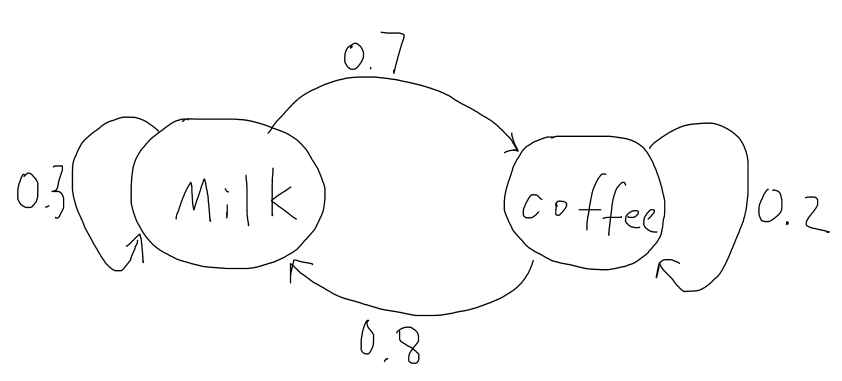
As you can see from the diagram, if the person drinks milk today there is a 30% chance he will drink it again tomorrow and there is a 70% chance he will drink coffee tomorrow.
What can we do with this?
Transition probabilities and Transition Matrix
We define Pij to be the probability that the future state is j given the present state is i.
P(Xn + 1 = j | Xn = i) = Pi'j
They are called transition distributions. If a Markov Chain’s transition distributions do not depend on n (just like the above example), then we can say the Markov Chain has stationary transition distributions.
In particular, a Markov Chain with stationary transition distributions can be represented by a Transition Matrix. For instance, the transition Matrix for the above Example is:
$ \begin{pmatrix} 0.3 & 0.7 \\ 0.8 & 0.2 \end{pmatrix} $
More Generally:$ P=\begin{bmatrix} P_{11} & \cdots & P_{1k} \\ \vdots & \ddots & \vdots \\ P_{k1} & \cdots & P_{kk} \end{bmatrix} $
General Rule for nth state distribution:xn = xn − 1P
Important Notes:
Pi'j in the above matrix represents P(Xn + 1 = j | Xn = i), it turns out that the the sum of the entries in each row is 1 (This follows the same notation as my probability textbook and most of the professional articles I have found with online libraries). However, in some textbooks (for example, my linear algebra textbook) and resources I have found on the Internet, Pi'j in the Matrix = P(Xn + 1 = i | Xn = j), this means the sum of every entry in each column is 1. To avoid confusion, we are going to follow the first notation style in this note.
The transition matrix makes computations in a Markov Chain much easier. In the breakfast example above (stationary transition probability), if we are given that a person drinks milk at time n,Xn = 1, we can determine the probability distribution of Xn + 3. The initial state distribution can be written as a row vector : $ \begin{pmatrix}1 & 0\end{pmatrix} $
$ x_{n+3}=x_{n+2}P=(x_{n+1}P)P=((x_nP)P)P=x_nP^3=\begin{pmatrix}1 & 0\end{pmatrix} \begin{pmatrix} 0.3 & 0.7 \\ 0.8 & 0.2 \end{pmatrix}^3 $
$ x_{n+3}=\begin{pmatrix}0.475 & 0.525\end{pmatrix} $
This means given the person drinks milk today, three days later, there is a 47.5% chance he will drink milk and a 52.5% he will drink coffee.
- Matrix Limits and Markov Chains
In the Linear Algebra courses (MA351 and MA353 at Purdue University), we learn that a diagonalizable Matrix A can be represented in the form A = Q'D'Q − 1.
Where $ D=\begin{bmatrix} r_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & r_n \end{bmatrix} $, where r1...rn are eigenvalues of the matrix A, and Q are has columns corresponding to the eigenvectors.
$ A^n=QDQ^{-1}QDQ^{-1}...QDQ^{-1}=QD^nQ^{-1}; \lim_{n \to \infty}A^n=\lim_{n \to \infty}(QD^nQ^{-1}) $.
Since D is a diagonal matrix, it’s very easy to compute its powers. In the breakfast example above, we are able to compute the matrix limits.
$ P=\begin{pmatrix} 0.3 & 0.7 \\ 0.8 & 0.2 \end{pmatrix} $;
The Characteristic Polynomial for P is:
$ (0.3-r)(0.2-r)-0.8*0.7=0; r_1=1; r_2=-0.5; Thus,D=\begin{pmatrix} 1 & 0 \\ 0 & -0.5 \end{pmatrix} $
Solving the linear systems, eigenvectors for P are:
$ \begin{pmatrix} 1 \\ 1 \end{pmatrix} and \begin{pmatrix} 7 \\ -8 \end{pmatrix}; Thus, Q=\begin{pmatrix} 1 & 7 \\ 1 & -8 \end{pmatrix} $;
$ \lim_{n \to \infty}P^n=\lim_{n \to \infty}(QD^nQ^{-1})=\lim_{n \to \infty}\begin{pmatrix} 1 & 7 \\ 1 & -8 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -0.5 \end{pmatrix}^n \begin{pmatrix} 1 & 7 \\ 1 & -8 \end{pmatrix}^{-1} $
$ =\lim_{n \to \infty}\begin{pmatrix} (8+7(-0.5)^n)/15 & 7/15 \\ (8-8(-0.5)^n)/15 &(7-8(-0.5)^n)/15 \end{pmatrix}= \begin{pmatrix} 8/15 & 7/15 \\ 8/15 & 7/15 \end{pmatrix} $
We put the initial condition into the equation:
$ \begin{pmatrix} 1 & 0 \end{pmatrix}\begin{pmatrix} 8/15 & 7/15 \\ 8/15 & 7/15 \end{pmatrix}=\begin{pmatrix} 8/15 & 7/15 \end{pmatrix} $
In fact, we will always get $ \begin{pmatrix} 8/15 & 7/15 \end{pmatrix} $ whether he drinks milk or coffee on the first day. This indicates that over a long time period, he will drink milk in 8/15 of days, and drink coffee in 7/15 of days.
Use MatLab to verify our result, just use n=1000: 
3. Why are people talking about Markov Chains?
- Applications of Markov Chains in Science and Real Life
Markov Chains have lots of applications in scientific research, because many things can be modeled using Markov Chains. In economics and finance, Markov Chains can help investors predict the volatility of asset returns. In biology, Markov chains can be used in population genetics research. In the simplest cases, Markov chains can be used in weather predictions.
We now construct a very simple sample case of weather prediction. Assume a city's weather has 3 distinct states: Sunny, Rainy and Overcast. These states, respectively, have the following sample space S= {0,1,2}. Suppose that the probability distribution of the next day only depends on the weather state of today (This is relatively reasonable in real cases), and given that:
P(Xn + 1 = S'u'n'n'y | Xn = S'u'n'n'y) = 0.5;
P(Xn + 1 = R'a'i'n'y | Xn = S'u'n'n'y) = 0.2;
P(Xn + 1 = O'v'e'r'c'a's't | Xn = S'u'n'n'y) = 1 − 0.5 − 0.2 = 0.3;
P(Xn + 1 = S'u'n'n'y | Xn = R'a'i'n'y) = 0.6;
P(Xn + 1 = R'a'i'n'y | Xn = R'a'i'n'y) = 0.3;
P(Xn + 1 = O'v'e'r'c'a's't | Xn = R'a'i'n'y) = 1 − 0.6 − 0.3 = 0.1;
P(Xn + 1 = S'u'n'n'y | Xn = O'v'e'r'c'a's't) = 0.2;
P(Xn + 1 = R'a'i'n'y | Xn = O'v'e'r'c'a's't) = 0.6;
P(Xn + 1 = O'v'e'r'c'a's't | Xn = O'v'e'r'c'a's't) = 1 − 0.2 − 0.6 = 0.2; 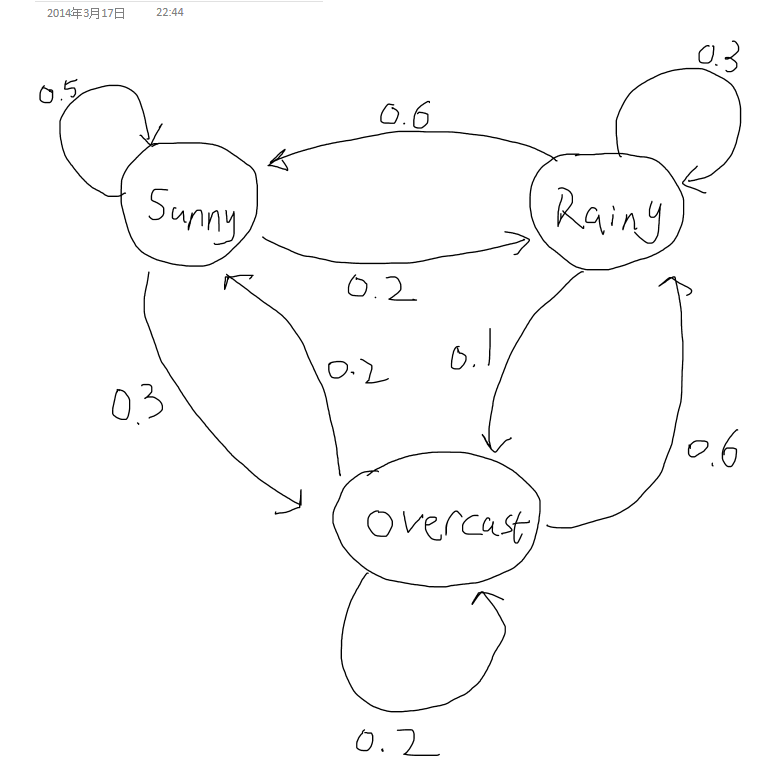
Transition Matrix P for this Model:
$ \begin{pmatrix} 0.5 & 0.2 & 0.3 \\ 0.6 & 0.3 & 0.1 \\ 0.2 & 0.6 & 0.2 \\ \end{pmatrix} $
Suppose we know the weather is overcast on Monday (Today), then we can determine the probability distribution of weather over the next several days (weather forecasting). For instance, on Wednesday:
$ x_{n+2}=x_{n}P^2=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0.5 & 0.2 & 0.3 \\ 0.6 & 0.3 & 0.1 \\ 0.2 & 0.6 & 0.2 \\ \end{pmatrix} \begin{pmatrix} 0.5 & 0.2 & 0.3 \\ 0.6 & 0.3 & 0.1 \\ 0.2 & 0.6 & 0.2 \\ \end{pmatrix} =\begin{pmatrix} 0.5 & 0.34 & 0.16 \end{pmatrix} $
This means on Wednesday, the probability is 0.5 for sunny, 0.34 for rainy and 0.16 for overcast given that Monday is overcast.
We can also use matrix limits to determine the long-term probability following the procedure in Part II. Since it’s little bit complicated to diagonalize a 3*3 matrix by hand, especially for a matrix with complex eigenvalues and eigenvectors, we use Matlab instead: 
$ \lim_{n \to \infty}P^n=\lim_{n \to \infty}(QD^nQ^{-1})=\begin{pmatrix} 50/107 & 34/107 & 23/107 \\ 50/107 & 34/107 & 23/107 \\ 50/107 & 34/107 & 23/107 \\ \end{pmatrix} $
Therefore, for a single day randomly picked from the calendar, this city has a probability of 50/107 of sunny weather, 34/107 for rainy weather and 23/107 for overcast weather. Verify this result with Matlab, take n=10000: 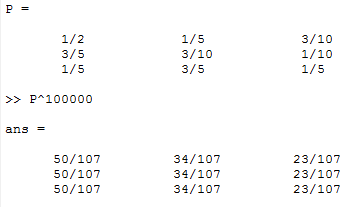
Application in PageRank 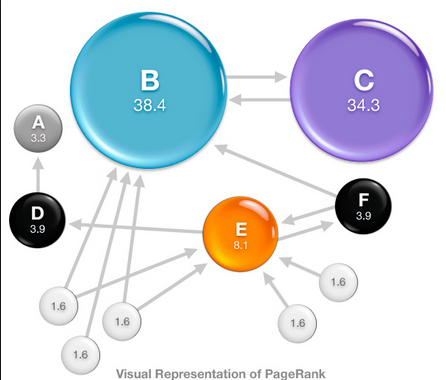
One of the significant application involving Markov chains is PageRank. As demonstrated in the picture, it is a simulation of the Probability that surfer will visit each webpage at time t. Actually, the process is more complicated. To simplify it, we just consider the basic idea of Markov Chain, we assume that for each step, the surfer can either follow the links on the current website or jump randomly to another website in the network(the number of website is constant n). Namely, with probability P, the surfer will follow the link on the current website, and with chance of (1-P), he will jump to websites which have no link on the current website.
In order to have a glimpse of how it works. We attach the codes of our team member's CS class as follows.
Suppose P = 0.75 and n = 5
web1 has link on web4,
web2 has link on web1,
web3 has link on web1,
web4 has links on web2, web3 and web5,
web5 has link on web3
numsims = 5000; % Parameter controlling the number of simulations
G = [0 0 0 1 0; 1 0 0 0 0; 1 0 0 0 0; 0 1 1 0 1; 0 0 1 0 0];
n = length(G); % size of network
state = 1; % initial state of the system
p = 0.75; % probability of following link on web page
M = zeros(n,n); % create the matrix of probabilities
for i = 1:n;
for j = 1:n;
M(i,j) = p*G(i,j)/sum(G(i,:)) + (1-p)/n;
end
end
pages = zeros(1,n); % vector to hold number of times page visited
% Simulate a surfer's session for i=1:numsims
prob = rand;
if prob < M(state,1)
state = 1;
elseif prob < M(state,1) + M(state,2)
state = 2;
elseif prob < M(state,1) + M(state,2) + M(state,3)
state = 3;
elseif prob < M(state,1) + M(state,2) + M(state,3) + M(state,4)
state = 4;
else state = 5;
end;
pages(state) = pages(state) + 1;
if ~mod(i,numsims/5)
fprintf('%6d %5.3f %5.3f %5.3f %5.3f %5.3f \n',i,pages/sum(pages));
end
end 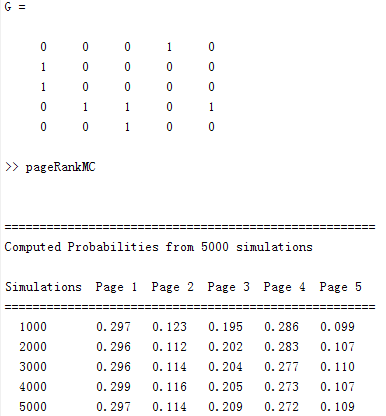
If we increase the number of simulation to 500000, we can see a more stable pattern.
The results is
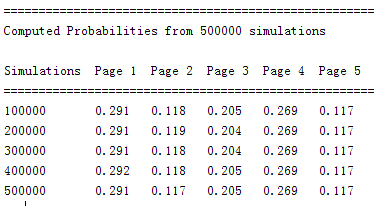
This shows an important concept within Markov Chains: steady-state probabilities. After a significant number of transitions, the process will fall into a general pattern and the initial state will no longer have an affect on the final state. Rather, each final state will be given a probability that is independent of the initial state. This can be clearly seen in the Page Rank code output above with the increasingly large number of transitions.
Discussion: Even Markov Chain is great idea in this PageRank simulation example, there are still some challenge things we need to improve. First, the number of pages on the internet is not constant. Secondly, the links of on each webpage will change. Thirdly, the probability actually is really hard to be a constant. That is why we need other theories to improve our strategy, like Time Series and Stochastic Process.
The weather model and PageRank made by us are very simple examples of the real applications of Markov Chains. Many other models, such as prediction on genetic illness, also use Markov Chains. Yet they are too complex to show on this webpage.
In addition to the previous discrete applications of Markov Chain, continuous applications are just as important. Continuous Markov Chains are frequently used within queuing theory. Frequently service systems are modeled as a Markov Chain where the states are the number of customers in the system. Customer interarrival times are often modeled as an exponential variable where λ is the rate at which the number of customers (system state) increases by 1. Then the model can specify the number of servers and the various distributions of service times where a completed service will reduce the number of customers in the system by one. A Markov Chain model is very powerful because through using matrix calculations, one can extract very important properties of their modeled system crucial to decision making. A user will be able to determine average time that customers are in the system, time they are in the queue, and the average number of busy servers (just to name a few). From there, important decisions can be made regarding how to manage the modeled system such as how many servers to have (staffing decision) or how large to make a waiting room (queue size).
This project was originally conducted by Office Word, a link for the PDF file (already uploaded to this site) can be found
Courses which group members have taken that are relevant to this project: IE336 (Operations Research – Stochastic Modeling), MA416(Probability), STAT417(Statistical Inference), MA 353 (Linear Algebra II), CS 314 (Numerical Methods), IE581(Simulation Design & Analysis). These courses have provided a large range of knowledge ranging from direct applications of Markov Chains to computing necessary matrix calculations important to Markov Chains.
References and Theorems & knowledge Sources:
- Morris H. Degroot, Mark J. Schervish, Probability and Statistics, 4th edition
- Michael J. Evans, Jeffery S. Rosenthal, Probability and Statistics: The Science of Uncertainty, 2nd edition
- Stephen H. Friedberg, Arnold J. Insel, Linear Algebra, 4th edition
- Anne Greenbaum & Timothy P. Chartier, Numerical Methods, 1st edition

