(104 intermediate revisions by 5 users not shown)
Line 1: Line 1:
−
<h1>
+
= Ballots: what is out there? =
−
Ballots: what is out there?
+
−
</h1>
+
  
−
<p>
+
A team project for [[2013 Fall MA 279 Walther|MA279, Fall 2013]]  
−
A team project for [[2013 Fall MA 279 Walther|MA279, Fall 2013]]
+
−
</p>
+
  
−
<p>
+
Team members: Qianyu Deng, Sui Fang, Weichen Gai, Chenkai Wang, Bolun Zhang  
−
Team members: Qianyu Deng, Sui Fang, Weichen Gai, Chenkai Wang, Bolun Zhang
+
−
</p>
+
  
−
<hr>
+
----
  
−
<h2>
+
== Introduction (Chenkai Wang)  ==
−
Introduction
+
−
</h2>
+
  
−
<p>
+
The main purpose of using ballots in an election is to record the opinions of electorates and their preferences of the candidates. The goal is to determine a winner from the candidates. Ballots come in many physical forms, such as a piece of paper or a digital document stored in a computer. The actual format of a ballot is called voting system or voting method. A voting system has several built-in rules in order to ensure fair voting during the election. Another functionality of a voting system is counting the voting from ballots to determine a final winner. So to specify a valid voting system, we have to describe two key ingredients: allowable votes, i.e., ballots and the algorithms of collecting votes. In this study, we will study how various voting systems are designed and reveal the mathematical reasons in designing these voting systems. <!--There’s other voting ballots that have been used. (i.e., Approval voting, Copeland Method, Kemeny-Young method…) Body(We introduce 3 or 4 method in this part)-->  
−
According to Wikipedia, a ballot is a device used to cast votes in an election. The main purpose of using ballots is to record the opinions of electorates and their preferences of the candidates. The goal is to determine a winner from the candidates. Ballots come in many physical forms, such as a piece of paper or a digital document stored in a computer. The actual format of a ballot is called voting system or voting method. In this study, we will study how various voting systems are designed and reveal the mathematical reasons in designing these voting systems.
+
−
</p>
+
−
<!--There’s other voting ballots that have been used. (i.e., Approval voting, Copeland Method, Kemeny-Young method…) Body(We introduce 3 or 4 method in this part)-->
+
  
−
<h2>
+
== Fairness Criteria ==
−
Fairness Criteria
+
−
</h2>
+
  
−
<p>
+
In order to minimize biased opinions in a voting system, we use fairness criteria to measure the "fairness" of a particular voting system. A fairness criteria is a mathematical description of the rules a voting systems uses. In a formal mathematical treatment, we can define the mathematical meaning of the word "fairness" according to these criteria. Here we describe three important criteria and end with Arrow's impossibility theorem. First, we have the following definition.
−
In order to minimize biased opinions in a voting system, we use fairness criteria to measure the "fairness" of a particular voting system. In a formal mathematical treatment, we can define the mathematical meaning of the word "fairness" according to these criteria.
+
−
</p>
+
  
−
<h3>
+
<u>Definition</u> Let <span class="texhtml">''C''</span> be the finite set of candidates and <span class="texhtml">''N''</span> be the finite set of voters. Let <span class="texhtml">''L''</span> be the set of all total (linear) ordering on <span class="texhtml">''C''</span>, i.e., it's the space of all possible ballots submitted by voters. Note since all underlying sets are finite, there is no difference between total ordering and well ordering. Each total ordering assigns a unique natural number <math>1\leq\mathrm{rank}(a)\leq|C|</math> to all candidates <math>a\in C</math> since a finite well ordering is isomorphic to a unique finite ordinal number. A social welfare function is a function <math>f:L^N\rightarrow L</math>. The domain of <span class="texhtml">''f''</span> is called the set of preference profiles. A generic element of <span class="texhtml">''L''<sup>''N''</sup></span> has the form <math>\langle \leq_1, \leq_2,\cdots,\leq_N \rangle</math>, where <math>\leq_i</math> are total ordering on <span class="texhtml">''C''</span>, i.e., one generic element (preference profile) represents a possible outcome of all voters. A social welfare function represents the process of choosing the winner from one generic preference profile, i.e., giving the final total ordering of the candidates. Let's denote <math>f(\leq_1,\cdots,\leq_N)</math> by the single symbol <math>\leq</math>.
−
Transitivity
+
−
</h3>
+
  
−
<hr>
+
=== Unanimity  ===
  
−
<h2>
+
<u>Definition</u> Let <math>a,b\in C</math>, if <math>\forall i\in N(a<_ib)</math>, then <span class="texhtml">''a'' &lt; ''b''</span>. In words, if every voters prefer one candidate to another, this order should be preserved in the final decision.
−
Method 1
+
−
</h2>
+
  
−
<ol>
+
=== Independence of Irrelevant Alternatives  ===
−
<li>Background
+
  
−
<p>
+
<u>Definition</u> Let <math>r,s\in L^N</math> and <math>a\in C</math>, if <span class="texhtml">rank<sub>''r''</sub>(''a'') = rank<sub>''s''</sub>(''a'')</span>, then <span class="texhtml">rank<sub>''f''(''r'')</sub>(''a'') = rank<sub>''f''(''s'')</sub>(''a'')</span>. In other words, if one candidate has the same ranks in two preference profiles, the rank should also be the same in two corresponding final decisions.
  
−
</p>
+
=== Non-dictatorship  ===
  
−
<li>Method
+
<u>Definition</u> There is no <math>i\in N</math> such that if <math>\langle\leq_1,\cdots,\leq_N\rangle\in L^N</math>, we have <math>f(\leq_1,\cdots,\leq_N)=\leq_i</math>. In words, the final decision should be different from all elements in a preference profile.
−
<li>Abortion reason
+
−
</ol>
+
  
−
<hr>
+
=== Arrow's Impossibility Theorem  ===
  
−
<h2>
+
<u>Theorem</u> ''There is no social welfare function satisfies the criteria of unanimity, independence of Irrelevant Alternatives, and non-dictatorship for candidates of size greater than three.''
−
Method 2
+
−
</h2>
+
  
−
<ol>
+
This theorem imposes a strong constraint on all possible voting systems. In layman's term, there can not be a perfect fair voting system if we need the above three fairness criteria. In the following study, we introduce some actual voting systems which are not on the textbook and demonstrate how they work and how Arrow's Impossibility Theorem applies on them.
−
<li>Background
+
−
<li>Method
+
−
<li>Abortion reason
+
−
</ol>
+
  
−
<hr>
+
----
  
−
<h2>
+
== Copeland Method (Sui Fang)  ==
−
Method 3
+
−
</h2>
+
  
−
<ol>
+
=== History  ===
−
<li>Background
+
−
<li>Method
+
−
<li>Abortion reason
+
−
</ol>
+
  
−
<h2>
+
Copeland method is a Condorcet method to elect winners by using pairwise comparison that the order of candidates is ranked by the difference between the number of pairwise wins and the number of pairwise loses. Supporters argue that this method is fairly understandable and practical in our daily life. Moreover, it is easy for us to calculate data and get results. However, others believe that this method cannot deal with all cases. “When there is Condorcet winner, Copeland method usually meets ties.”—(Wiki) In addition, opponents think this method pay too much attention to the number of rounds’ victories and defeats instead of quantities of voters for candidates. Then I will use an example from website to show how to apply this method and what criterion it fails.
−
Conclusion
+
−
</h2>
+
  
−
<hr>
+
=== How it works?  ===
  
−
<h2>
+
'''step1''' Find preference by voters
−
Bibliography
+
−
</h2>
+
  
−
<ol>
+
'''step2''' Pairwise Comparison
−
<li><i>Ballots</i>. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Ballot
+
−
<li>
+
−
</ol>
+
  
−
<hr>
+
'''step3''' Calculate (The # of wins – The # of loses)
−
[[2013_Fall_MA_279_Walther|Back to MA279 Fall 2013]]
+
  
−
[[Category:MA279Fall2013Walther]]
+
'''step4''' Ranking
−
[[Category:math]]
+
 
−
[[Category:project]]
+
Example:
 +
 
 +
“Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.”—(Wiki)
 +
 
 +
<br>Step1:Find preference by voters
 +
 
 +
{| border="1"
 +
|-
 +
! 42% of voters(close to Memphis)
 +
! 26% of voters(close to Nashville)
 +
! 15% of voters(close to Chattanooga)
 +
! 17% of voters(close to Knoxville)
 +
|-
 +
|
 +
#Memphis
 +
#Nashville
 +
#Chattanooga
 +
#Knoxville
 +
 
 +
|
 +
#Nashville
 +
#Chattanooga
 +
#Knoxville
 +
#Memphis
 +
 
 +
|
 +
#Chattanooga
 +
#Knoxville
 +
#Nashville
 +
#Memphis
 +
 
 +
|
 +
#Knoxville
 +
#Chattanooga
 +
#Nashville
 +
#Memphis
 +
 
 +
|}
 +
 
 +
<br>Step2:Pairwise Comparison
 +
 
 +
{| border="1"
 +
|-
 +
! Comparison
 +
! Result
 +
! Winner
 +
|-
 +
| Memphis vs Nashville
 +
| 42vs58
 +
| Nashville
 +
|-
 +
| Memphis vs Knoxville
 +
| 42vs58
 +
| Knoxville
 +
|-
 +
| Memphis vs Chattanooga
 +
| 42 vs 58
 +
| Chattanooga
 +
|-
 +
| Nashville vs Knoxville
 +
| 68 vs 32
 +
| Nashville
 +
|-
 +
| Nashville vs Chattanooga
 +
| 68 vs 32
 +
| Nashville
 +
|-
 +
| Knoxville vs Chattanooga
 +
| 17 vs 83
 +
| Chattanooga
 +
|}
 +
 
 +
<br>Step3:Calculate (The # of wins – The # of loses)
 +
 
 +
{| border="1"
 +
|-
 +
! Candidate
 +
! Wins
 +
! Losses
 +
! Wins-Losses
 +
|-
 +
| Memphis
 +
| 0
 +
| 3
 +
| -3
 +
|-
 +
| Nashville
 +
| 3
 +
| 0
 +
| 3
 +
|-
 +
| Knoxville
 +
| 1
 +
| 2
 +
| -1
 +
|-
 +
| Chattanooga
 +
| 2
 +
| 1
 +
| 1
 +
|}
 +
 
 +
<br>Step4:Ranking
 +
 
 +
{| border="1"
 +
|-
 +
! Rank
 +
|-
 +
| 1.Nashville
 +
|-
 +
| 2.Chattanooga
 +
|-
 +
| 3.Knoxville
 +
|-
 +
| 4.Memphis
 +
|}
 +
 
 +
According to result we get, we find that the order of candidates is the same as the table column2 (26% of voters close to Nashville) in step1. Hence, it doesn't satisfy the Non-dictator criteria.
 +
 
 +
----
 +
 
 +
== Kemeny-Young Method (Qianyu Deng)  ==
 +
 
 +
=== History  ===
 +
 
 +
Kemeny-Young method is a voting system first developed by John Kemeny in 1959 and showed as the unique neutral method satisfying reinforcement and the Condorcet Criterion by Peyton Young and Arthur Levenglick in 1978. It uses preferential ballots and pairwise comparison to find the most popular ranking in an election. This method satisfying Condorcet Criterion since if there is a Condorcet winner, then it is always the most popular one.
 +
 
 +
<br>
 +
 
 +
=== How it works?  ===
 +
 
 +
'''step1''' pairwise comparison
 +
 
 +
'''step2''' Create a tally table of the pairwise comparison
 +
 
 +
'''step3''' Count ranking score
 +
 
 +
'''step4''' Find the ranking which gets the highest ranking score
 +
 
 +
Now,let's look at the previous example of the election on the location of capital of Tennessee we use before to see how it works.
 +
 
 +
<br>
 +
 
 +
=== Example  ===
 +
 
 +
{| border="1"
 +
|-
 +
! 42% of voters(close to Memphis)
 +
! 26% of voters(close to Nashville)
 +
! 15% of voters(close to Chattanooga)
 +
! 17% of voters(close to Knoxville)
 +
|-
 +
|
 +
#Memphis
 +
#Nashville
 +
#Chattanooga
 +
#Knoxville
 +
 
 +
|
 +
#Nashville
 +
#Chattanooga
 +
#Knoxville
 +
#Memphis
 +
 
 +
|
 +
#Chattanooga
 +
#Knoxville
 +
#Nashville
 +
#Memphis
 +
 
 +
|
 +
#Knoxville
 +
#Chattanooga
 +
#Nashville
 +
#Memphis
 +
 
 +
|}
 +
 
 +
'''Step1''':Find the pairwise comparison in terms of the population percentage
 +
 
 +
{| border="1"
 +
|-
 +
|
 +
| over Memphis
 +
| over Nashville
 +
| over Chattanooga
 +
| over Knoxville
 +
|-
 +
| prefer Memphis
 +
| \
 +
| 42%
 +
| 42%
 +
| 42%
 +
|-
 +
| prefer Nashville
 +
| 58%
 +
| \
 +
| 68%
 +
| 68%
 +
|-
 +
| prefer Chattanooga
 +
| 58%
 +
| 32%
 +
| \
 +
| 83%
 +
|-
 +
| prefer Knoxville
 +
| 58%
 +
| 32%
 +
| 17%
 +
| \
 +
|}
 +
 
 +
'''Step 2''': Create a tally table of the pairwise comparison
 +
 
 +
{| border="1"
 +
|-
 +
|
 +
| prefer X over Y
 +
| equal preference
 +
| prefer Y over X
 +
|-
 +
| X = Memphis,Y = Nashville
 +
| 42%
 +
| 0
 +
| 58%
 +
|-
 +
| X = Memphis,Y = Chattanooga
 +
| 42%
 +
| 0
 +
| 58%
 +
|-
 +
| X = Memphis,Y = Knoxville
 +
| 42%
 +
| 0
 +
| 58%
 +
|-
 +
| X = Nashville,Y = Chattanooga
 +
| 68%
 +
| 0
 +
| 32%
 +
|-
 +
| X = Nashville,Y = Knoxville
 +
| 68%
 +
| 0
 +
| 32%
 +
|-
 +
| X = ChattanoogaY = Knoxville
 +
| 83%
 +
| 0
 +
| 17%
 +
|}
 +
 
 +
'''Step3''': Count ranking score <br>Suppose we want to calculate the ranking score of the following ranking:
 +
 
 +
{| border="1"
 +
|-
 +
| 1st
 +
| Memphis
 +
|-
 +
| 2nd
 +
| Nashville
 +
|-
 +
| 3rd
 +
| Chattanooga
 +
|-
 +
| 4th
 +
| Knoxville
 +
|}
 +
 
 +
This ranking satisfies the preferences Memphis&gt;Nashville, Memphis&gt;Chattanooga, Memphis&gt;Knoxville, Nashville&gt;Chattanooga, Nashville&gt; Knoxville, Chattanooga&gt;Knoxville.The respective score, according to the tally table, are: <br>Memphis&gt;Nashville&nbsp;: 42 <br>Memphis&gt;Chattanooga: 42 <br>Memphis&gt;Knoxville: 42 <br>Nashville&gt;Chattanooga: 68 <br>Nashville&gt; Knoxville: 68 <br>Chattanooga&gt;Knoxville: 83 <br>So, 42+42+42+68+68+83 = 345. <br>Continuing calculating in this way, we can get the following table of all possible ranking score:
 +
<br>Here, we denote Memphis as M, Nashville as N, Chattanooga as C, and Knoxville as K in abbreviation.
 +
 
 +
{| border="1"
 +
|-
 +
! 1st Choice
 +
! 2nd Choice
 +
! 3rd Choice
 +
! 4th Choice
 +
! ranking score
 +
|-
 +
| M
 +
| N
 +
| C
 +
| K
 +
| 345
 +
|-
 +
| M
 +
| N
 +
| K
 +
| C
 +
| 279
 +
|-
 +
| M
 +
| C
 +
| N
 +
| K
 +
| 309
 +
|-
 +
| M
 +
| C
 +
| K
 +
| N
 +
| 273
 +
|-
 +
| M
 +
| K
 +
| N
 +
| C
 +
| 243
 +
|-
 +
| M
 +
| K
 +
| C
 +
| N
 +
| 207
 +
|-
 +
| N
 +
| M
 +
| C
 +
| K
 +
| 361
 +
|-
 +
| N
 +
| M
 +
| K
 +
| C
 +
| 295
 +
|-
 +
| N
 +
| C
 +
| M
 +
| K
 +
| 377
 +
|-
 +
| N
 +
| C
 +
| K
 +
| M
 +
| 393
 +
|-
 +
| N
 +
| K
 +
| M
 +
| C
 +
| 311
 +
|-
 +
| N
 +
| K
 +
| C
 +
| M
 +
| 327
 +
|-
 +
| C
 +
| M
 +
| N
 +
| K
 +
| 325
 +
|-
 +
| C
 +
| M
 +
| K
 +
| N
 +
| 289
 +
|-
 +
| C
 +
| N
 +
| M
 +
| K
 +
| 341
 +
|-
 +
| c
 +
| N
 +
| K
 +
| M
 +
| 357
 +
|-
 +
| C
 +
| K
 +
| M
 +
| N
 +
| 305
 +
|-
 +
| C
 +
| K
 +
| N
 +
| M
 +
| 321
 +
|-
 +
| K
 +
| M
 +
| N
 +
| C
 +
| 259
 +
|-
 +
| K
 +
| M
 +
| C
 +
| N
 +
| 223
 +
|-
 +
| K
 +
| N
 +
| M
 +
| C
 +
| 275
 +
|-
 +
| K
 +
| N
 +
| C
 +
| M
 +
| 291
 +
|-
 +
| K
 +
| C
 +
| M
 +
| N
 +
| 239
 +
|-
 +
| K
 +
| C
 +
| N
 +
| M
 +
| 255
 +
|}
 +
 
 +
'''Step4''': Find the ranking which gets the highest ranking score. <br>we see that the highest ranking score is 393 which is the score of the ranking of
 +
 
 +
{| border="1"
 +
|-
 +
| 1st
 +
| Nashville
 +
|-
 +
| 2nd
 +
| Chattanooga
 +
|-
 +
| 3rd
 +
| Knoxville
 +
|-
 +
| 4th
 +
| Memphis
 +
|}
 +
<p> According to the ranking result, we can see that this method fails to satisfy non-dictatorship criterion like the previous method does.</p>
 +
 
 +
----
 +
 
 +
== Schulze Method (Weichen Gai)  ==
 +
 
 +
=== History  ===
 +
 
 +
The Schulze method, also known as Schwartz Sequential Dropping (SSD), was developed in 1997 by Markus Schulze in order to select a single winner but can also apply to select a list of winners. It was first used in public mailing list in 1997-1998 and then widely adpoted.
 +
 
 +
=== How it works?  ===
 +
 
 +
'''step 1''' Pairwise comparison
 +
 
 +
'''step 2''' Create a matrix of pairwise preferences. (We can color the cell with green if d[X,Y]&gt;d[Y,X], otherwise color it with red for better visualization.)
 +
 
 +
'''step 3''' Identify the strongest paths and the strengths of each paths.
 +
 
 +
'''step 4''' Ranking.
 +
 
 +
=== Example &nbsp;  ===
 +
 
 +
In the following example 45 voters rank 5 candidates.
 +
 
 +
*5 ACBED
 +
*5 ADECB
 +
*8 BEDAC
 +
*3 CABED
 +
*7 CAEBD
 +
*2 CBADE
 +
*7 DCEBA
 +
*8 EBADC
 +
 
 +
'''Step 1.&nbsp;'''Pairwise comparison
 +
 
 +
For example, when comparing B and C, there are 8+8=16 voters who prefer B to C. So d[B,C]=16.
 +
 
 +
'''Step 2:'''&nbsp;Create a matrix of pairwise preferences
 +
 
 +
{| width="200" border="1" cellpadding="1" cellspacing="1"
 +
|+ Matrix of Pairwise Preferences
 +
|-
 +
| <br>
 +
| d[*,A]
 +
| d[*,B]
 +
| d[*,C]
 +
| d[*,D]
 +
| d[*,E]
 +
|-
 +
| d[A,*]
 +
|
 +
| 20
 +
| 26
 +
| 30
 +
| 22
 +
|-
 +
| d[B,*]
 +
| 25
 +
|
 +
| 16
 +
| 33
 +
| 18
 +
|-
 +
| d[C,*]
 +
| 19
 +
| 29
 +
|
 +
| 17
 +
| 24
 +
|-
 +
| d[D,*]
 +
| 15
 +
| 12
 +
| 28
 +
|
 +
| 14
 +
|-
 +
| d[E,*]
 +
| 23
 +
| 27
 +
| 21
 +
| 31
 +
|
 +
|}
 +
 
 +
'''Step 3:'''&nbsp;Identify the strongest paths and the strengths of each paths.
 +
 
 +
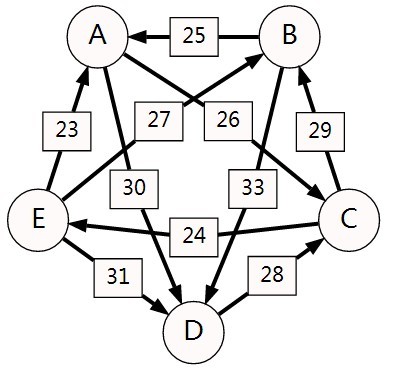
[[Image:Schulze.jpg]]<br>
 +
 
 +
Each direction of an arrow is determined the value of d[X,Y] and d[Y,X]. The arrow points at X if d[X,Y]&gt;d[Y,X] and vice versa.
 +
 
 +
From the picture we can see that, for instance, if we want to determine the strongest path from A to C, we have two options, A-C or A-D-C. The strength of each path is the value of its weakest link. In this case, the strongest path from A to C is A-D-C that has strenth 28&gt; that of A-C, which has strenth 26.
 +
 
 +
'''Step 4:''' Ranking
 +
 
 +
From step 3 we have the strength of each strongest path.
 +
 
 +
{| width="200" border="1" cellpadding="1" cellspacing="1"
 +
|+ Strengths of the strongest paths
 +
|-
 +
|
 +
| p[*,A]
 +
| p[*,B]
 +
| p[*,C]
 +
| p[*,D]
 +
| p[*,E]
 +
|-
 +
| p[A,*]
 +
|
 +
| 28
 +
| 28
 +
| 28
 +
| 30
 +
|-
 +
| p[B,*]
 +
| 25
 +
|
 +
| 28
 +
| 33
 +
| 24
 +
|-
 +
| p[C,*]
 +
| 25
 +
| 29
 +
|
 +
| 29
 +
| 24
 +
|-
 +
| p[D,*]
 +
| 25
 +
| 28
 +
| 28
 +
|
 +
| 24
 +
|-
 +
| p[E,*]
 +
| 25
 +
| 28
 +
| 28
 +
| 31
 +
|
 +
|}
 +
 
 +
The winner is X between X and Y if p[X,Y]&gt;p[Y,X]. For example, the winner is C since p[C,D]=29&gt;p[D,C]=28.
 +
 
 +
As a result, the Schulze ranking is E&gt;A&gt;C&gt;B&gt;D.
 +
 
 +
----
 +
 
 +
== Instant-runoff Voting Method (Bolun Zhang)  ==
 +
 
 +
=== History  ===
 +
 
 +
Instant runoff voting was devised in 1871 by American architect William Robert Ware, although it is, in effect, a special case of the single transferable vote system, which emerged independently in the 1850s. Unlike the single transferable vote in multi-seat elections, however, the only ballot transfers are from backers of candidates who have been eliminated.
 +
 
 +
<br>
 +
 
 +
=== How it works?  ===
 +
 
 +
'''step1''' Count the first-place votes for each candidate.
 +
 
 +
'''step2''' Eliminate the candidate with the fewest first-place votes.
 +
 
 +
'''step3''' Count ranking score
 +
 
 +
'''step4''' Repeat the process until there is a candidate with a majority of first-place votes.
 +
 
 +
<br>
 +
 
 +
=== Example  ===
 +
 
 +
{| border="1"
 +
|-
 +
! 42% of voters(close to Memphis)
 +
! 26% of voters(close to Nashville)
 +
! 15% of voters(close to Chattanooga)
 +
! 17% of voters(close to Knoxville)
 +
|-
 +
|
 +
#Memphis
 +
#Nashville
 +
#Chattanooga
 +
#Knoxville
 +
 
 +
|
 +
#Nashville
 +
#Chattanooga
 +
#Knoxville
 +
#Memphis
 +
 
 +
|
 +
#Chattanooga
 +
#Knoxville
 +
#Nashville
 +
#Memphis
 +
 
 +
|
 +
#Knoxville
 +
#Chattanooga
 +
#Nashville
 +
#Memphis
 +
 
 +
|}
 +
 
 +
<br> '''Step1''': Count the first place votes for each candidate. Memphis 42%<br> Nashville 26%<br> Chattanooga 15%<br> Knoxville 17%<br><br> '''Step2''': Eliminate the candidate with the fewest first-place votes.<br> Chattanooga is eliminated
 +
 
 +
'''Rearrange the ballots''':
 +
 
 +
{| border="1"
 +
|-
 +
! 42% of voters(close to Memphis)
 +
! 26% of voters(close to Nashville)
 +
! 32% of voters(close to Knoxville)
 +
|-
 +
|
 +
#Memphis
 +
#Nashville
 +
#Knoxville
 +
 
 +
|
 +
#Nashville
 +
#Knoxville
 +
#Memphis
 +
 
 +
|
 +
#Knoxville
 +
#Nashville
 +
#Memphis
 +
 
 +
|}
 +
 
 +
<br> '''Step3''': Repeat the process: Count the first place votes for each candidate.<br> Memphis 42%<br> Nashville 26%<br> Knoxville 32%<br> Nashville gets the fewest first-place votes and is eliminated.
 +
 
 +
'''Rearrange the ballot''':
 +
 
 +
{| border="1"
 +
|-
 +
! 42% of voters (close to Memphis)
 +
! 32% of voters (close to Knoxville)
 +
|-
 +
|
 +
#Memphis
 +
#Knoxville
 +
 
 +
|
 +
#Knoxville
 +
#Memphis
 +
 
 +
|}
 +
 
 +
<br>Count the first-place votes for each candidates.<br> Memphis 42%<br> Knoxville 58%<br><br> Knoxville gets 58% votes over a half, which means Knoxville has a majority of first-place votes.<br><br> '''Knoxville is the winner'''.<br> <br> Therefore it does not satisfy Independence of Irrelevant Alternatives criteria.<br>
 +
 
 +
<br>
 +
 
 +
 
 +
 
 +
----
 +
 
 +
== Bibliography  ==
 +
 
 +
#''Ballots''. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Ballot
 +
#''Copeland''. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Copeland's_method
 +
#''Schulze Method''. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Schulze_method
 +
#''Instant-runoff voting''. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Instant-runoff_voting
 +
 
 +
----
 +
 
 +
[[2013 Fall MA 279 Walther|Back to MA279 Fall 2013]]
 +
 
 +
[[Category:MA279Fall2013Walther]] [[Category:Math]] [[Category:Project]]

Latest revision as of 17:36, 1 December 2013

Ballots: what is out there?

A team project for MA279, Fall 2013

Team members: Qianyu Deng, Sui Fang, Weichen Gai, Chenkai Wang, Bolun Zhang

Introduction (Chenkai Wang)

The main purpose of using ballots in an election is to record the opinions of electorates and their preferences of the candidates. The goal is to determine a winner from the candidates. Ballots come in many physical forms, such as a piece of paper or a digital document stored in a computer. The actual format of a ballot is called voting system or voting method. A voting system has several built-in rules in order to ensure fair voting during the election. Another functionality of a voting system is counting the voting from ballots to determine a final winner. So to specify a valid voting system, we have to describe two key ingredients: allowable votes, i.e., ballots and the algorithms of collecting votes. In this study, we will study how various voting systems are designed and reveal the mathematical reasons in designing these voting systems.

Fairness Criteria

In order to minimize biased opinions in a voting system, we use fairness criteria to measure the "fairness" of a particular voting system. A fairness criteria is a mathematical description of the rules a voting systems uses. In a formal mathematical treatment, we can define the mathematical meaning of the word "fairness" according to these criteria. Here we describe three important criteria and end with Arrow's impossibility theorem. First, we have the following definition.

Definition Let C be the finite set of candidates and N be the finite set of voters. Let L be the set of all total (linear) ordering on C, i.e., it's the space of all possible ballots submitted by voters. Note since all underlying sets are finite, there is no difference between total ordering and well ordering. Each total ordering assigns a unique natural number $ 1\leq\mathrm{rank}(a)\leq|C| $ to all candidates $ a\in C $ since a finite well ordering is isomorphic to a unique finite ordinal number. A social welfare function is a function $ f:L^N\rightarrow L $. The domain of f is called the set of preference profiles. A generic element of LN has the form $ \langle \leq_1, \leq_2,\cdots,\leq_N \rangle $, where $ \leq_i $ are total ordering on C, i.e., one generic element (preference profile) represents a possible outcome of all voters. A social welfare function represents the process of choosing the winner from one generic preference profile, i.e., giving the final total ordering of the candidates. Let's denote $ f(\leq_1,\cdots,\leq_N) $ by the single symbol $ \leq $.

Unanimity

Definition Let $ a,b\in C $, if $ \forall i\in N(a<_ib) $, then a < b. In words, if every voters prefer one candidate to another, this order should be preserved in the final decision.

Independence of Irrelevant Alternatives

Definition Let $ r,s\in L^N $ and $ a\in C $, if rankr(a) = ranks(a), then rankf(r)(a) = rankf(s)(a). In other words, if one candidate has the same ranks in two preference profiles, the rank should also be the same in two corresponding final decisions.

Non-dictatorship

Definition There is no $ i\in N $ such that if $ \langle\leq_1,\cdots,\leq_N\rangle\in L^N $, we have $ f(\leq_1,\cdots,\leq_N)=\leq_i $. In words, the final decision should be different from all elements in a preference profile.

Arrow's Impossibility Theorem

Theorem There is no social welfare function satisfies the criteria of unanimity, independence of Irrelevant Alternatives, and non-dictatorship for candidates of size greater than three.

This theorem imposes a strong constraint on all possible voting systems. In layman's term, there can not be a perfect fair voting system if we need the above three fairness criteria. In the following study, we introduce some actual voting systems which are not on the textbook and demonstrate how they work and how Arrow's Impossibility Theorem applies on them.

Copeland Method (Sui Fang)

History

Copeland method is a Condorcet method to elect winners by using pairwise comparison that the order of candidates is ranked by the difference between the number of pairwise wins and the number of pairwise loses. Supporters argue that this method is fairly understandable and practical in our daily life. Moreover, it is easy for us to calculate data and get results. However, others believe that this method cannot deal with all cases. “When there is Condorcet winner, Copeland method usually meets ties.”—(Wiki) In addition, opponents think this method pay too much attention to the number of rounds’ victories and defeats instead of quantities of voters for candidates. Then I will use an example from website to show how to apply this method and what criterion it fails.

How it works?

step1 Find preference by voters

step2 Pairwise Comparison

step3 Calculate (The # of wins – The # of loses)

step4 Ranking

Example:

“Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.”—(Wiki)


Step1:Find preference by voters

42% of voters(close to Memphis) 26% of voters(close to Nashville) 15% of voters(close to Chattanooga) 17% of voters(close to Knoxville)
  1. Memphis
  2. Nashville
  3. Chattanooga
  4. Knoxville
  1. Nashville
  2. Chattanooga
  3. Knoxville
  4. Memphis
  1. Chattanooga
  2. Knoxville
  3. Nashville
  4. Memphis
  1. Knoxville
  2. Chattanooga
  3. Nashville
  4. Memphis


Step2:Pairwise Comparison

Comparison Result Winner
Memphis vs Nashville 42vs58 Nashville
Memphis vs Knoxville 42vs58 Knoxville
Memphis vs Chattanooga 42 vs 58 Chattanooga
Nashville vs Knoxville 68 vs 32 Nashville
Nashville vs Chattanooga 68 vs 32 Nashville
Knoxville vs Chattanooga 17 vs 83 Chattanooga


Step3:Calculate (The # of wins – The # of loses)

Candidate Wins Losses Wins-Losses
Memphis 0 3 -3
Nashville 3 0 3
Knoxville 1 2 -1
Chattanooga 2 1 1


Step4:Ranking

Rank
1.Nashville
2.Chattanooga
3.Knoxville
4.Memphis

According to result we get, we find that the order of candidates is the same as the table column2 (26% of voters close to Nashville) in step1. Hence, it doesn't satisfy the Non-dictator criteria.

Kemeny-Young Method (Qianyu Deng)

History

Kemeny-Young method is a voting system first developed by John Kemeny in 1959 and showed as the unique neutral method satisfying reinforcement and the Condorcet Criterion by Peyton Young and Arthur Levenglick in 1978. It uses preferential ballots and pairwise comparison to find the most popular ranking in an election. This method satisfying Condorcet Criterion since if there is a Condorcet winner, then it is always the most popular one.


How it works?

step1 pairwise comparison

step2 Create a tally table of the pairwise comparison

step3 Count ranking score

step4 Find the ranking which gets the highest ranking score

Now,let's look at the previous example of the election on the location of capital of Tennessee we use before to see how it works.


Example

42% of voters(close to Memphis) 26% of voters(close to Nashville) 15% of voters(close to Chattanooga) 17% of voters(close to Knoxville)
  1. Memphis
  2. Nashville
  3. Chattanooga
  4. Knoxville
  1. Nashville
  2. Chattanooga
  3. Knoxville
  4. Memphis
  1. Chattanooga
  2. Knoxville
  3. Nashville
  4. Memphis
  1. Knoxville
  2. Chattanooga
  3. Nashville
  4. Memphis

Step1:Find the pairwise comparison in terms of the population percentage

over Memphis over Nashville over Chattanooga over Knoxville
prefer Memphis \ 42% 42% 42%
prefer Nashville 58% \ 68% 68%
prefer Chattanooga 58% 32% \ 83%
prefer Knoxville 58% 32% 17% \

Step 2: Create a tally table of the pairwise comparison

prefer X over Y equal preference prefer Y over X
X = Memphis,Y = Nashville 42% 0 58%
X = Memphis,Y = Chattanooga 42% 0 58%
X = Memphis,Y = Knoxville 42% 0 58%
X = Nashville,Y = Chattanooga 68% 0 32%
X = Nashville,Y = Knoxville 68% 0 32%
X = ChattanoogaY = Knoxville 83% 0 17%

Step3: Count ranking score
Suppose we want to calculate the ranking score of the following ranking:

1st Memphis
2nd Nashville
3rd Chattanooga
4th Knoxville

This ranking satisfies the preferences Memphis>Nashville, Memphis>Chattanooga, Memphis>Knoxville, Nashville>Chattanooga, Nashville> Knoxville, Chattanooga>Knoxville.The respective score, according to the tally table, are:
Memphis>Nashville : 42
Memphis>Chattanooga: 42
Memphis>Knoxville: 42
Nashville>Chattanooga: 68
Nashville> Knoxville: 68
Chattanooga>Knoxville: 83
So, 42+42+42+68+68+83 = 345.
Continuing calculating in this way, we can get the following table of all possible ranking score:
Here, we denote Memphis as M, Nashville as N, Chattanooga as C, and Knoxville as K in abbreviation.

1st Choice 2nd Choice 3rd Choice 4th Choice ranking score
M N C K 345
M N K C 279
M C N K 309
M C K N 273
M K N C 243
M K C N 207
N M C K 361
N M K C 295
N C M K 377
N C K M 393
N K M C 311
N K C M 327
C M N K 325
C M K N 289
C N M K 341
c N K M 357
C K M N 305
C K N M 321
K M N C 259
K M C N 223
K N M C 275
K N C M 291
K C M N 239
K C N M 255

Step4: Find the ranking which gets the highest ranking score.
we see that the highest ranking score is 393 which is the score of the ranking of

1st Nashville
2nd Chattanooga
3rd Knoxville
4th Memphis

According to the ranking result, we can see that this method fails to satisfy non-dictatorship criterion like the previous method does.

Schulze Method (Weichen Gai)

History

The Schulze method, also known as Schwartz Sequential Dropping (SSD), was developed in 1997 by Markus Schulze in order to select a single winner but can also apply to select a list of winners. It was first used in public mailing list in 1997-1998 and then widely adpoted.

How it works?

step 1 Pairwise comparison

step 2 Create a matrix of pairwise preferences. (We can color the cell with green if d[X,Y]>d[Y,X], otherwise color it with red for better visualization.)

step 3 Identify the strongest paths and the strengths of each paths.

step 4 Ranking.

Example  

In the following example 45 voters rank 5 candidates.

  • 5 ACBED
  • 5 ADECB
  • 8 BEDAC
  • 3 CABED
  • 7 CAEBD
  • 2 CBADE
  • 7 DCEBA
  • 8 EBADC

Step 1. Pairwise comparison

For example, when comparing B and C, there are 8+8=16 voters who prefer B to C. So d[B,C]=16.

Step 2: Create a matrix of pairwise preferences

Matrix of Pairwise Preferences

d[*,A] d[*,B] d[*,C] d[*,D] d[*,E]
d[A,*] 20 26 30 22
d[B,*] 25 16 33 18
d[C,*] 19 29 17 24
d[D,*] 15 12 28 14
d[E,*] 23 27 21 31

Step 3: Identify the strongest paths and the strengths of each paths.

Schulze.jpg

Each direction of an arrow is determined the value of d[X,Y] and d[Y,X]. The arrow points at X if d[X,Y]>d[Y,X] and vice versa.

From the picture we can see that, for instance, if we want to determine the strongest path from A to C, we have two options, A-C or A-D-C. The strength of each path is the value of its weakest link. In this case, the strongest path from A to C is A-D-C that has strenth 28> that of A-C, which has strenth 26.

Step 4: Ranking

From step 3 we have the strength of each strongest path.

Strengths of the strongest paths
p[*,A] p[*,B] p[*,C] p[*,D] p[*,E]
p[A,*] 28 28 28 30
p[B,*] 25 28 33 24
p[C,*] 25 29 29 24
p[D,*] 25 28 28 24
p[E,*] 25 28 28 31

The winner is X between X and Y if p[X,Y]>p[Y,X]. For example, the winner is C since p[C,D]=29>p[D,C]=28.

As a result, the Schulze ranking is E>A>C>B>D.

Instant-runoff Voting Method (Bolun Zhang)

History

Instant runoff voting was devised in 1871 by American architect William Robert Ware, although it is, in effect, a special case of the single transferable vote system, which emerged independently in the 1850s. Unlike the single transferable vote in multi-seat elections, however, the only ballot transfers are from backers of candidates who have been eliminated.


How it works?

step1 Count the first-place votes for each candidate.

step2 Eliminate the candidate with the fewest first-place votes.

step3 Count ranking score

step4 Repeat the process until there is a candidate with a majority of first-place votes.


Example

42% of voters(close to Memphis) 26% of voters(close to Nashville) 15% of voters(close to Chattanooga) 17% of voters(close to Knoxville)
  1. Memphis
  2. Nashville
  3. Chattanooga
  4. Knoxville
  1. Nashville
  2. Chattanooga
  3. Knoxville
  4. Memphis
  1. Chattanooga
  2. Knoxville
  3. Nashville
  4. Memphis
  1. Knoxville
  2. Chattanooga
  3. Nashville
  4. Memphis


Step1: Count the first place votes for each candidate. Memphis 42%
Nashville 26%
Chattanooga 15%
Knoxville 17%

Step2: Eliminate the candidate with the fewest first-place votes.
Chattanooga is eliminated

Rearrange the ballots:

42% of voters(close to Memphis) 26% of voters(close to Nashville) 32% of voters(close to Knoxville)
  1. Memphis
  2. Nashville
  3. Knoxville
  1. Nashville
  2. Knoxville
  3. Memphis
  1. Knoxville
  2. Nashville
  3. Memphis


Step3: Repeat the process: Count the first place votes for each candidate.
Memphis 42%
Nashville 26%
Knoxville 32%
Nashville gets the fewest first-place votes and is eliminated.

Rearrange the ballot:

42% of voters (close to Memphis) 32% of voters (close to Knoxville)
  1. Memphis
  2. Knoxville
  1. Knoxville
  2. Memphis


Count the first-place votes for each candidates.
Memphis 42%
Knoxville 58%

Knoxville gets 58% votes over a half, which means Knoxville has a majority of first-place votes.

Knoxville is the winner.

Therefore it does not satisfy Independence of Irrelevant Alternatives criteria.



Bibliography

  1. Ballots. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Ballot
  2. Copeland. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Copeland's_method
  3. Schulze Method. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Schulze_method
  4. Instant-runoff voting. Retrieved from Wikipedia: http://en.wikipedia.org/wiki/Instant-runoff_voting

Back to MA279 Fall 2013

Retrieved from "https://www.projectrhea.org/rhea/index.php?title=Walther279Fall13_Topic3&oldid=61276"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

ECE462 Survivor

Seraj Dosenbach