(New page: == Intro to Public Key Cryptography == Public key cryptography also known as asymmetric cryptography refers to a cryptographic algorithm which requires two separate keys one of which is ...) |
|||
| Line 1: | Line 1: | ||
== Intro to Public Key Cryptography == | == Intro to Public Key Cryptography == | ||
| − | Public key cryptography also known as asymmetric cryptography refers to a cryptographic algorithm which requires two separate keys one of which is secret and one of which is public. Although different, the two parts of this key pair are mathematically linked. The public key is used to encrypt plaintext or to verify a digital signature; whereas the private key is used to decrypt ciphertext or to create a digital signature. The term "asymmetric" stems from the use of different keys to perform these opposite functions, each the inverse of the other.<br> <br>Cryptography is a way for two people, commonly referred to as Alice (A) and Bob (B), to communicate over an insecure communications channel without an opponent, Eve (E), intercepting what is being said. It provides the foundation for key management and digital signatures, both integral parts of any cryptosystem. Below is a pictorial representation illustrating the general idea of key exchange. | + | Public key cryptography also known as asymmetric cryptography refers to a cryptographic algorithm which requires two separate keys one of which is secret and one of which is public. Although different, the two parts of this key pair are mathematically linked. The public key is used to encrypt plaintext or to verify a digital signature; whereas the private key is used to decrypt ciphertext or to create a digital signature. The term "asymmetric" stems from the use of different keys to perform these opposite functions, each the inverse of the other.<br> <br>Cryptography is a way for two people, commonly referred to as Alice (A) and Bob (B), to communicate over an insecure communications channel without an opponent, Eve (E), intercepting what is being said. It provides the foundation for key management and digital signatures, both integral parts of any cryptosystem. Below is a pictorial representation illustrating the general idea of key exchange.<br> |
| − | + | ||
| − | <br> | + | |
[[Image:Alice bob.png]] | [[Image:Alice bob.png]] | ||
| Line 21: | Line 19: | ||
<u></u> <u>Principle of Operation</u> | <u></u> <u>Principle of Operation</u> | ||
| − | <u></u> Public and private keys:<br>Alice and Bob each have a key, some number or mathematical procedure that can be applied to messages, composed of a public piece and a private piece. The private pieces of these keys are never transmitted, while the public pieces are accessible to everyone.<br> <br>Based on mathematics:<br>Public-key algorithms are based on mathematical problems which currently admit no efficient solution that are inherent in certain integer factorization, discrete logarithm, and elliptic curve relationships.<br> <br>Authentication:<br>Alice and Bob may also have public and private signatures, which work similarly to the keys. If Alice wants Bob to know that the message he receives from her is authentic, she’ll apply a private signature to some authentication message before sending it; when Bob wants to know that it’s hers, he’ll apply the easily accessible public part of her signature to that, which will return the authentication.<u></u> <u> | + | <u></u> Public and private keys:<br>Alice and Bob each have a key, some number or mathematical procedure that can be applied to messages, composed of a public piece and a private piece. The private pieces of these keys are never transmitted, while the public pieces are accessible to everyone.<br> <br>Based on mathematics:<br>Public-key algorithms are based on mathematical problems which currently admit no efficient solution that are inherent in certain integer factorization, discrete logarithm, and elliptic curve relationships.<br> <br>Authentication:<br>Alice and Bob may also have public and private signatures, which work similarly to the keys. If Alice wants Bob to know that the message he receives from her is authentic, she’ll apply a private signature to some authentication message before sending it; when Bob wants to know that it’s hers, he’ll apply the easily accessible public part of her signature to that, which will return the authentication.<u></u><u></u><br> |
| − | <u></u> | + | <u>Asymmetric </u><u></u><u></u><u>Cryptography Systems</u><u></u><br> |
| − | + | First Generation:<br>Internet communications have been secured by the first generation of public key cryptographic algorithms developed in the mid-1970's. Notably, they form the basis for key management and authentication for IP encryption (IKE/IPSEC), web traffic (SSL/TLS) and secure electronic mail. Examples of such are the Diffie – Hellman and RSA methods.<br> <br>Diffie-Hellman:<br>Diffie–Hellman key exchange (D–H) is a specific method of exchanging cryptographic keys. It is a first generation of key exchange implemented within the field of cryptography. The Diffie–Hellman key exchange method allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure communications channel. This key can then be used to encrypt subsequent communications using a symmetric key cipher, so that a third party cannot intercept the message. The Diffie-Hellman method makes use of certain one-way functions called trap-door functions, to make it almost impossible to decipher encrypted data without a key.<br> <br>RSA:<br>Known as one of the first practicable public-key cryptosystems and is yet widely used for secure data transmission. In RSA, this asymmetry is based on the practical difficulty of factoring the product of two large prime numbers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described the algorithm in 1977.<br> | |
== <br> '''Intro to elliptic curves in public key crypto''' == | == <br> '''Intro to elliptic curves in public key crypto''' == | ||
| Line 32: | Line 30: | ||
[[Image:Key size.png]] | [[Image:Key size.png]] | ||
| − | |||
| − | |||
Also, in another paper The Advantages of Elliptic Curve Cryptography For Wireless Security written by K. Lauter in February 2004, she wrote “Wireless devices are rapidly becoming more dependent on security features such as the ability to do secure email, secure Web browsing, and virtual private networking to corporate networks, and ECC allows more efficient implementation of all of these features.” So ECC is particularly crucial in small cards or portable devices where CPU consumption, battery life and memory usage are limited. In this high-technology era, ECC is extremely wild used. | Also, in another paper The Advantages of Elliptic Curve Cryptography For Wireless Security written by K. Lauter in February 2004, she wrote “Wireless devices are rapidly becoming more dependent on security features such as the ability to do secure email, secure Web browsing, and virtual private networking to corporate networks, and ECC allows more efficient implementation of all of these features.” So ECC is particularly crucial in small cards or portable devices where CPU consumption, battery life and memory usage are limited. In this high-technology era, ECC is extremely wild used. | ||
Revision as of 16:26, 24 November 2013
Intro to Public Key Cryptography
Public key cryptography also known as asymmetric cryptography refers to a cryptographic algorithm which requires two separate keys one of which is secret and one of which is public. Although different, the two parts of this key pair are mathematically linked. The public key is used to encrypt plaintext or to verify a digital signature; whereas the private key is used to decrypt ciphertext or to create a digital signature. The term "asymmetric" stems from the use of different keys to perform these opposite functions, each the inverse of the other.
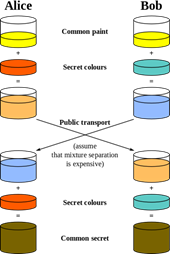
Cryptography is a way for two people, commonly referred to as Alice (A) and Bob (B), to communicate over an insecure communications channel without an opponent, Eve (E), intercepting what is being said. It provides the foundation for key management and digital signatures, both integral parts of any cryptosystem. Below is a pictorial representation illustrating the general idea of key exchange.
Usage / Current Applications
Key Management:
Key Management entails the generation, exchange, storage, use, and replacement of keys. It includes cryptographic protocol design, key servers, user procedures, and other relevant protocols. Successful key management is critical to the security of a cryptosystem.
Digital Signatures:
A digital signature is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, such that the sender cannot deny having sent the message and that the message was not altered in transit.
Principle of Operation
Public and private keys:
Alice and Bob each have a key, some number or mathematical procedure that can be applied to messages, composed of a public piece and a private piece. The private pieces of these keys are never transmitted, while the public pieces are accessible to everyone.
Based on mathematics:
Public-key algorithms are based on mathematical problems which currently admit no efficient solution that are inherent in certain integer factorization, discrete logarithm, and elliptic curve relationships.
Authentication:
Alice and Bob may also have public and private signatures, which work similarly to the keys. If Alice wants Bob to know that the message he receives from her is authentic, she’ll apply a private signature to some authentication message before sending it; when Bob wants to know that it’s hers, he’ll apply the easily accessible public part of her signature to that, which will return the authentication.
Asymmetric Cryptography Systems
First Generation:
Internet communications have been secured by the first generation of public key cryptographic algorithms developed in the mid-1970's. Notably, they form the basis for key management and authentication for IP encryption (IKE/IPSEC), web traffic (SSL/TLS) and secure electronic mail. Examples of such are the Diffie – Hellman and RSA methods.
Diffie-Hellman:
Diffie–Hellman key exchange (D–H) is a specific method of exchanging cryptographic keys. It is a first generation of key exchange implemented within the field of cryptography. The Diffie–Hellman key exchange method allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure communications channel. This key can then be used to encrypt subsequent communications using a symmetric key cipher, so that a third party cannot intercept the message. The Diffie-Hellman method makes use of certain one-way functions called trap-door functions, to make it almost impossible to decipher encrypted data without a key.
RSA:
Known as one of the first practicable public-key cryptosystems and is yet widely used for secure data transmission. In RSA, this asymmetry is based on the practical difficulty of factoring the product of two large prime numbers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described the algorithm in 1977.
Intro to elliptic curves in public key crypto
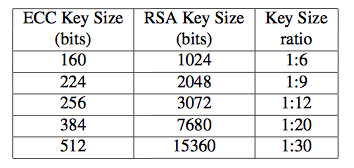
In 1985, two American mathematician Neal Koblitz and Victor S. Miller suggested the use of elliptic curves in cryptography for the first time independently. Before this, another algorithm called Rivest-Shamir-Adleman (RSA) is already published in 1970s. RSA is the very first well-established public key cryptosystem and it is wildly used after publishing. Elliptic Curve Cryptography (ECC) often used to compare with RSA after Koblitz and Miller suggested it. According to an IEEE article Performance Analysis of Identity Management in the Session Initiation Protocol by Rebahi, Pallares, Nguyen and etc, ECC encryption only need 160-bit keys to provide equivalent level of security while RSA encryption needs 1024 bits. More details for the key size is shown in the following table:
Also, in another paper The Advantages of Elliptic Curve Cryptography For Wireless Security written by K. Lauter in February 2004, she wrote “Wireless devices are rapidly becoming more dependent on security features such as the ability to do secure email, secure Web browsing, and virtual private networking to corporate networks, and ECC allows more efficient implementation of all of these features.” So ECC is particularly crucial in small cards or portable devices where CPU consumption, battery life and memory usage are limited. In this high-technology era, ECC is extremely wild used.
Even though ECC is efficient, it has a few drawbacks just like other algorithms. ECC requires more complicated operation than RSA, so it is harder to verify whether a specific implementation is correct or not. Therefore ECC has higher possibility of operation errors. However, ECC is still one of the most efficient and popular cryptography so far.