| Line 129: | Line 129: | ||
Compute the following expression: | Compute the following expression: | ||
| − | <font size=4><math> \ | + | <font size=4><math> \iint(x^2+y^2)dA </math></font> |
| − | where dA is the region bounded by | + | where dA is the region bounded by y<sup>2</sup>-x<sup>2</sup>=9, y<sup>2</sup>-x<sup>2</sup>=16, 2xy=14, 2xy=6. |
====Solution:==== | ====Solution:==== | ||
| Line 139: | Line 139: | ||
[[Image:JacobianPic3.png]] | [[Image:JacobianPic3.png]] | ||
| − | let <math> | + | let <math>v=2xy, ~~~~ u=y^2-x^2</math>. |
| − | Why do we do this? Let's look at the bounds: they're from | + | Why do we do this? Let's look at the bounds: they're from y<sup>2</sup>-x<sup>2</sup> =9 to y<sup>2</sup> -x<sup>2</sup>=16 and 2xy=6 and 2xy=14.It'd be quite a simple task if the integral looked something like this: |
<math> \int^{16}_9 \int^{14}_6 k(u,v)\mathrm{d}u\mathrm{d}v</math> | <math> \int^{16}_9 \int^{14}_6 k(u,v)\mathrm{d}u\mathrm{d}v</math> | ||
| Line 150: | Line 150: | ||
<math>u=2xy\longrightarrow \frac{\partial u}{\partial x}= 2y , \; \frac{\partial u}{\partial y} = 2x</math> | <math>u=2xy\longrightarrow \frac{\partial u}{\partial x}= 2y , \; \frac{\partial u}{\partial y} = 2x</math> | ||
| − | <math>v= | + | <math>v=y^2-x^2\longrightarrow \frac{\partial v}{\partial x}= -2x , \; \frac{\partial v}{\partial y} =2y</math> |
</font> | </font> | ||
| Line 159: | Line 159: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
2y & 2x \\ | 2y & 2x \\ | ||
| − | 2x & | + | -2x & 2y\end{bmatrix} |
</math> | </math> | ||
| − | <math> dxdy=\left|J(u,v)\right| | + | <math> dxdy=\left|J(u,v)\right| *dudv |
| + | =\left|\begin{bmatrix} | ||
| + | 2y & 2x \\ | ||
| + | 2x & -2y\end{bmatrix}\right|*dudv=(4y^2+4x^2)dudv </math> | ||
| + | Therefore, the new region looks like this: | ||
| + | [[Image: JacobianPic4.png]] | ||
| + | Therefore, | ||
| + | <math>\iint(x^2+y^2)dA=\int^{16}_9 \int^{14}_6 (x^2+y^2)/(4y^2+4x^2)\mathrm{d}u\mathrm{d}v=\int^{16}_9 \int^{14}_6 1/4\mathrm{d}u\mathrm{d}v=(16-9)*(14-6)*1/4=7/2. | ||
| + | |||
| + | ====Example #5:==== | ||
| + | Compute the following expression: | ||
| + | |||
| + | <font size=4><math> \iint(sqrt(4x^2+9y^2))dA </math></font> | ||
| + | |||
| + | where dA is the region bounded by (2x)<sup>2</sup>+(3y)<sup>2</sup>=36. | ||
| + | |||
| + | ====Solution:==== | ||
| + | Again, let's graph the region. | ||
| + | [[Image: JacobianPic5.png]] | ||
Revision as of 09:13, 9 May 2013
Contents
Jacobians and their applications
by Joseph Ruan, proud Member of the Math Squad.
Basic Definition
The Jacobian Matrix is just a matrix that takes the partial derivatives of each element of a transformation. In general, the Jacobian Matrix of a transformation F, looks like this:
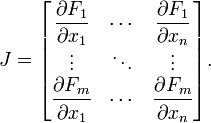 F1,F2, F3... are each of the elements of the output vector and x1,x2, x3 ... are each of the elements of the input vector.
F1,F2, F3... are each of the elements of the output vector and x1,x2, x3 ... are each of the elements of the input vector.
So for example, in a 2 dimensional case, let T be a transformation such that T(u,v)=<x,y> then the Jacobian matrix of this function would look like this:
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} $
This Jacobian matrix noticably holds all of the partial derivatives of the transformation with respect to each of the variables. Therefore each row contains how a particular output element changes with respect to each of the input elements. This means that the Jacobian matrix contains vectors that help describe how a change in any of the input elements affects the output elements.
To help illustrate making Jacobian matrices, let's do some examples:
Example #1:
What would be the Jacobian Matrix of this Transformation? $ T(u,v) = <u\times \cos v, u\times \sin v> $ .
Solution:
$ x=u \times \cos v \longrightarrow \frac{\partial x}{\partial u}= \cos v , \; \frac{\partial x}{\partial v} = -u\times \sin v $
$ y=u\times\sin v \longrightarrow \frac{\partial y}{\partial u}= \sin v , \; \frac{\partial y}{\partial v} = u\times \cos v $
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} \cos v & -u\times \sin v \\ \sin v & u\times \cos v \end{bmatrix} $
Example #2:
What would be the Jacobian Matrix of this Transformation?
$ T(u,v) = <u, v, u^v>,u>0 $ .
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=u \longrightarrow \frac{\partial x}{\partial u}= 1 , \; \frac{\partial x}{\partial v} = 0 $
$ y=v \longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} = 1 $
$ z=u^v \longrightarrow \frac{\partial y}{\partial u}= u^{v-1}\times v, \; \frac{\partial y}{\partial v} = u^v\times ln(u) $
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ u^{v-1}\times v & u^v\times ln(u)\end{bmatrix} $
Example #3:
What would be the Jacobian Matrix of this Transformation?
$ T(u,v) = <\tan (uv)> $ .
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=\tan(uv) \longrightarrow \frac{\partial x}{\partial u}= \sec^2(uv)\times v, \; \frac{\partial x}{\partial v} = sec^2(uv)\times u $
$ J(u,v)= \begin{bmatrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \end{bmatrix}=\begin{bmatrix}\sec^2(uv)\times v & sec^2(uv)\times u \end{bmatrix} $
Application: Jacaobian Determinants
The determinant of Example #1 gives:
$ \left|\begin{matrix} \cos v & -u \times \sin v \\ \sin v & u \times \cos v \end{matrix}\right|=~~ u \cos^2 v + u \sin^2 v =~~ u $
Notice that, in an integral when changing from cartesian coordinates (dxdy) to polar coordinates $ (drd\theta) $, the equation is as such:
$ dxdy=r\times drd\theta=u\times dudv $
It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely
$ dC1=det(J(T))dC2 $
where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates.
It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible. This makes sense because when changing coordinates, it should be possible to change back.
Moreover, recall from linear algebra that, in a two dimensional case, the determinant of a matrix of two vectors describes the area of the parallelogram drawn by it, or more accurately, it describes the scale factor between the unit square and the area of the parallelogram. If we extend the analogy, the determinant of the Jacobian would describe some sort of scale factor change from one set of coordinates to the other. Here is a picture that should help:
This is the general idea behind change of variables. It is easy to that the jacobian method matches up with one-dimensional change of variables:
$ T(u)=\begin{matrix}u^2\end{matrix}=\begin{matrix}x\end{matrix} $ $ ~~~,~~~~~~~~ J(u)=\begin{bmatrix}\frac{\partial x}{\partial u}\end{bmatrix}=\begin{bmatrix}2u\end{bmatrix} $$ ,~~~~~~~ dx=\left|J(u)\right|\times du=2u\times du $
Example #4:
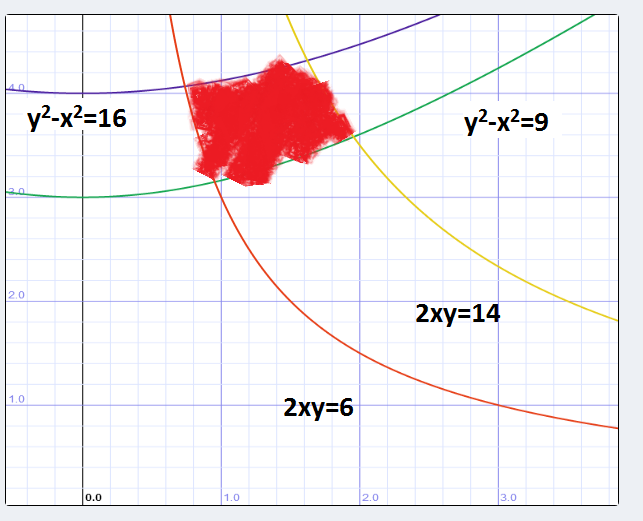
Compute the following expression:
$ \iint(x^2+y^2)dA $
where dA is the region bounded by y2-x2=9, y2-x2=16, 2xy=14, 2xy=6.
Solution:
First, let's graph the region.
let $ v=2xy, ~~~~ u=y^2-x^2 $.
Why do we do this? Let's look at the bounds: they're from y2-x2 =9 to y2 -x2=16 and 2xy=6 and 2xy=14.It'd be quite a simple task if the integral looked something like this:
$ \int^{16}_9 \int^{14}_6 k(u,v)\mathrm{d}u\mathrm{d}v $
Now, let's do the Jacobian.
$ u=2xy\longrightarrow \frac{\partial u}{\partial x}= 2y , \; \frac{\partial u}{\partial y} = 2x $
$ v=y^2-x^2\longrightarrow \frac{\partial v}{\partial x}= -2x , \; \frac{\partial v}{\partial y} =2y $
$ J(u,v)=\begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix}= \begin{bmatrix} 2y & 2x \\ -2x & 2y\end{bmatrix} $
$ dxdy=\left|J(u,v)\right| *dudv =\left|\begin{bmatrix} 2y & 2x \\ 2x & -2y\end{bmatrix}\right|*dudv=(4y^2+4x^2)dudv $
Therefore, the new region looks like this:

Therefore,
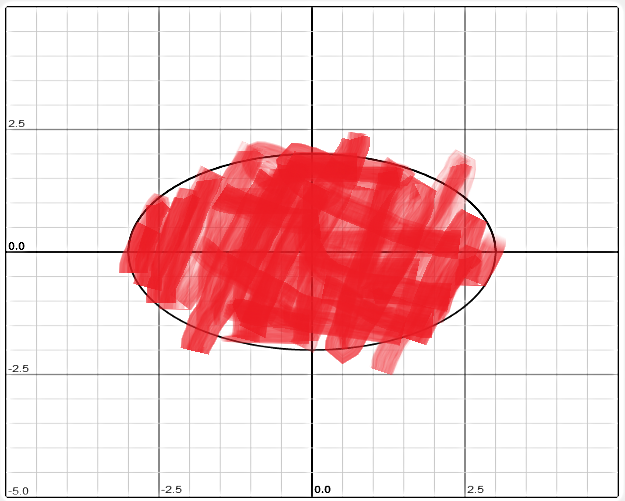
$ \iint(x^2+y^2)dA=\int^{16}_9 \int^{14}_6 (x^2+y^2)/(4y^2+4x^2)\mathrm{d}u\mathrm{d}v=\int^{16}_9 \int^{14}_6 1/4\mathrm{d}u\mathrm{d}v=(16-9)*(14-6)*1/4=7/2. ====Example #5:==== Compute the following expression: <font size=4><math> \iint(sqrt(4x^2+9y^2))dA $</font>
where dA is the region bounded by (2x)2+(3y)2=36.
Solution:
Again, let's graph the region.
Sources:
Rhea's Summer 2013 Math Squad was supported by an anonymous gift. If you enjoyed reading this tutorial, please help Rhea "help students learn" with a donation to this project. Your contribution is greatly appreciated.