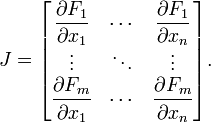| Line 16: | Line 16: | ||
[[Image:JacobianGen.png]] | [[Image:JacobianGen.png]] | ||
| − | <math> F_1,~~F_2,~~ F_3 </math>... are each of the elements of the output vector. | + | <math> F_1,~~F_2,~~ F_3 </math>... are each of the elements of the output vector. |
| − | <math> x_1,~~x_2,~~ x_3 </math> ... are each of the elements of the input vector. | + | <math> x_1,~~x_2,~~ x_3 </math> ... are each of the elements of the input vector. |
| − | + | So for example, in a 2 dimensional case, let T be a transformation such that | |
| − | + | ||
<font size=4><math>T(u,v)=<x,y> </math></font> | <font size=4><math>T(u,v)=<x,y> </math></font> | ||
| − | |||
then the Jacobian matrix of this function would look like this: | then the Jacobian matrix of this function would look like this: | ||
| Line 32: | Line 30: | ||
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}</math> | \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}</math> | ||
| − | + | To help illustrate making Jacobian matrices, let's do some examples: | |
| − | + | ||
| − | To help illustrate | + | |
==== Example #1: ==== | ==== Example #1: ==== | ||
Let's take the Transformation: | Let's take the Transformation: | ||
| + | |||
<font size=4><math>T(u,v) = <u * \cos v,r * \sin v> </math> </font>. | <font size=4><math>T(u,v) = <u * \cos v,r * \sin v> </math> </font>. | ||
| + | |||
What would be the Jacobian Matrix of this Transformation? | What would be the Jacobian Matrix of this Transformation? | ||
| Line 67: | Line 65: | ||
==== Example #2: ==== | ==== Example #2: ==== | ||
Let's take the Transformation: | Let's take the Transformation: | ||
| + | |||
<font size=4><math>T(u,v) = <u, v, u+v> </math> </font>. | <font size=4><math>T(u,v) = <u, v, u+v> </math> </font>. | ||
| + | |||
What would be the Jacobian Matrix of this Transformation? | What would be the Jacobian Matrix of this Transformation? | ||
| Line 92: | Line 92: | ||
1 & 1\end{bmatrix} | 1 & 1\end{bmatrix} | ||
</math> | </math> | ||
| + | |||
| + | |||
| + | ==== Example #3: ==== | ||
| + | Let's take the Transformation: | ||
| + | |||
| + | <font size=4><math>T(u,v) = <uv> </math> </font>. | ||
| + | |||
| + | What would be the Jacobian Matrix of this Transformation? | ||
| + | |||
| + | ===Solution:=== | ||
| + | Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective. | ||
| + | |||
| + | <font size = 4> | ||
| + | <math>x=u \longrightarrow \frac{\partial x}{\partial u}= v , \; \frac{\partial x}{\partial v} = u</math> | ||
| + | |||
| + | |||
| + | </font> | ||
| + | |||
| + | Therefore the Jacobian matrix is | ||
| + | |||
| + | <math>\begin{bmatrix} | ||
| + | \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \end{bmatrix}= | ||
| + | \begin{bmatrix} | ||
| + | v & u \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| Line 116: | Line 142: | ||
where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates. | where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates. | ||
| − | It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible. | + | It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible. This makes sense because |
| + | |||
| − | |||
---- | ---- | ||
| + | Sources: | ||
| + | |||
| + | # [[http://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant|Wikipedia]] | ||
Revision as of 09:27, 8 May 2013
Contents
Jacobians and their applications
by Joseph Ruan
Basic Definition
The Jacobian Matrix is just a matrix that takes the partial derivatives of each element of a transformation. In general, the Jacobian Matrix of a transformation F, looks like this:
$ F_1,~~F_2,~~ F_3 $... are each of the elements of the output vector.
$ x_1,~~x_2,~~ x_3 $ ... are each of the elements of the input vector.
So for example, in a 2 dimensional case, let T be a transformation such that
$ T(u,v)=<x,y> $
then the Jacobian matrix of this function would look like this:
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} $
To help illustrate making Jacobian matrices, let's do some examples:
Example #1:
Let's take the Transformation:
$ T(u,v) = <u * \cos v,r * \sin v> $ .
What would be the Jacobian Matrix of this Transformation?
Solution:
$ x=u*\cos v \longrightarrow \frac{\partial x}{\partial u}= \cos v , \; \frac{\partial x}{\partial v} = -u*\sin v $
$ y=u*\sin v \longrightarrow \frac{\partial y}{\partial u}= \sin v , \; \frac{\partial y}{\partial v} = u*\cos v $
Therefore the Jacobian matrix is
$ \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} \cos v & -u*\sin v \\ \sin v & u*\cos v \end{bmatrix} $
This example actually showcased the transformation "T" as the change from polar coordinates into Cartesian coordinates.
Let's do another example.
Example #2:
Let's take the Transformation:
$ T(u,v) = <u, v, u+v> $ .
What would be the Jacobian Matrix of this Transformation?
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=u \longrightarrow \frac{\partial x}{\partial u}= 1 , \; \frac{\partial x}{\partial v} = 0 $
$ y=v \longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} = 1 $
$ z=u+v \longrightarrow \frac{\partial y}{\partial u}= 1 , \; \frac{\partial y}{\partial v} = 1 $
Therefore the Jacobian matrix is
$ \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1\end{bmatrix} $
Example #3:
Let's take the Transformation:
$ T(u,v) = <uv> $ .
What would be the Jacobian Matrix of this Transformation?
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=u \longrightarrow \frac{\partial x}{\partial u}= v , \; \frac{\partial x}{\partial v} = u $
Therefore the Jacobian matrix is
$ \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \end{bmatrix}= \begin{bmatrix} v & u \end{bmatrix} $
Application: Jacaobian Determinants
The determinant of Example #1 gives:
$ \left|\begin{matrix} \cos v & -u * \sin v \\ \sin v & u * \cos v \end{matrix}\right|=~~ u \cos^2 v + u \sin^2 v =~~ u $
Notice that, in an integral when changing from cartesian coordinates (dxdy) to polar coordinates $ (drd\theta) $, the equation is as such:
$ dxdy=r*drd\theta $
in this case, since $ u =r $ and $ v = \theta $, then
$ dxdy=u*dudv $
It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely
$ dC1=det(J(T))dC2 $
where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates.
It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible. This makes sense because
Sources:
- [[1]]