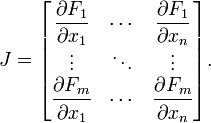| Line 55: | Line 55: | ||
This example actually showcased the transformation "T" as the change from polar coordinates into Cartesian coordinates. | This example actually showcased the transformation "T" as the change from polar coordinates into Cartesian coordinates. | ||
| + | |||
Let's do another example. | Let's do another example. | ||
| − | ===Example #2:=== Let | + | ==== Example #2: ==== |
| + | Let's take the Transformation: | ||
| + | <font size=4><math>T(u,v) = <u, v, u+v> </math> </font>. | ||
| + | What would be the Jacobian Matrix of this Transformation? | ||
| + | |||
| + | ===Solution:=== | ||
| + | Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective. | ||
| + | |||
| + | <font size = 4> | ||
| + | <math>x=u \longrightarrow \frac{\partial x}{\partial u}= 1 , \; \frac{\partial x}{\partial v} = 0</math> | ||
| + | |||
| + | <math>y=v \longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} = 1</math> | ||
| + | |||
| + | <math>z=u+v \longrightarrow \frac{\partial y}{\partial u}= 1 , \; \frac{\partial y}{\partial v} = 1</math> | ||
| + | </font> | ||
| + | |||
| + | Therefore the Jacobian matrix is | ||
| + | |||
| + | <math>\begin{bmatrix} | ||
| + | \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ | ||
| + | \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ | ||
| + | \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix}= | ||
| + | \begin{bmatrix} | ||
| + | 1 & 0 \\ | ||
| + | 0 & 1 \\ | ||
| + | 1 & 1\end{bmatrix} | ||
| + | </math> | ||
Revision as of 10:21, 8 May 2013
Contents
[hide]Jacobians and their applications
by Joseph Ruan
Basic Definition
The Jacobian Matrix is just a matrix that takes the partial derivatives of each element of a transformation (which is in the form of a vector. Let T be a transformation such that
$ T(u,v)=<x,y> $
then the Jacobian matrix of this function would look like this:
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} $
In general, the Jacobian Matrix of a Transformation F, looks like this:
To help illustrate this, let's do an example:
Example #1:
Let's take the Transformation: $ T(u,v) = <u * \cos v,r * \sin v> $ . What would be the Jacobian Matrix of this Transformation?
Solution:
$ x=u*\cos v \longrightarrow \frac{\partial x}{\partial u}= \cos v , \; \frac{\partial x}{\partial v} = -u*\sin v $
$ y=u*\sin v \longrightarrow \frac{\partial y}{\partial u}= \sin v , \; \frac{\partial y}{\partial v} = u*\cos v $
Therefore the Jacobian matrix is
$ \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} \cos v & -u*\sin v \\ \sin v & u*\cos v \end{bmatrix} $
This example actually showcased the transformation "T" as the change from polar coordinates into Cartesian coordinates.
Let's do another example.
Example #2:
Let's take the Transformation: $ T(u,v) = <u, v, u+v> $ . What would be the Jacobian Matrix of this Transformation?
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=u \longrightarrow \frac{\partial x}{\partial u}= 1 , \; \frac{\partial x}{\partial v} = 0 $
$ y=v \longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} = 1 $
$ z=u+v \longrightarrow \frac{\partial y}{\partial u}= 1 , \; \frac{\partial y}{\partial v} = 1 $
Therefore the Jacobian matrix is
$ \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1\end{bmatrix} $
Application: Jacaobian Determinants
The determinant of Example #1 gives:
$ \left|\begin{matrix} \cos v & -u * \sin v \\ \sin v & u * \cos v \end{matrix}\right|=~~ u \cos^2 v + u \sin^2 v =~~ u $
Notice that, in an integral when changing from cartesian coordinates (dxdy) to polar coordinates $ (drd\theta) $, the equation is as such:
$ dxdy=r*drd\theta $
in this case, since $ u =r $ and $ v = \theta $, then
$ dxdy=u*dudv $
It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely
$ dC1=det(J(T))dC2 $
where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates.
It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible.
For integrals, changing variables is quite useful. The most obvious case is that of u-substitution. However, for larger dimensions, this gets slightly trickier. Suppose we wanted to change