| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Linear | + | [[Category:bonus point project]] |
| + | [[Category:MA265]] | ||
| + | [[Category:linear algebra]] | ||
| + | |||
| + | <center><font size= 4> | ||
| + | '''Linear Programming''' | ||
| + | </font size> | ||
| + | |||
| + | Student project for [[MA265]] | ||
| + | </center> | ||
| + | ---- | ||
---- | ---- | ||
| | ||
'''What is linear programing?''' | '''What is linear programing?''' | ||
| + | ---- | ||
Linear programing is a mathematical method you can apply to find best possible results such as maximum profit or minimum cost. Linear programing practically use as one of the optimization problem solvers. In general, to solve a optimization problem, you need to have an objective (what do you want to solve? Do you want to maximize or minimize your function?) and constraints related to your function. Putting objective and constraints function together on a graph will generate a feasible region. | Linear programing is a mathematical method you can apply to find best possible results such as maximum profit or minimum cost. Linear programing practically use as one of the optimization problem solvers. In general, to solve a optimization problem, you need to have an objective (what do you want to solve? Do you want to maximize or minimize your function?) and constraints related to your function. Putting objective and constraints function together on a graph will generate a feasible region. | ||
For example, | For example, | ||
| + | |||
| + | Objective function | ||
| + | max -1/2x + 7 | ||
| + | |||
| + | Constraints | ||
| + | y=3x | ||
| + | y=x-2 | ||
[[Image:Linprog03.gif]] | [[Image:Linprog03.gif]] | ||
| + | (source: http://www.purplemath.com/modules/linprog.htm) | ||
| + | |||
| + | The shade area is the feasible region | ||
| Line 17: | Line 38: | ||
'''GAMS''' | '''GAMS''' | ||
| − | + | ---- | |
GAMS can be accessed through ITAP software remote (https://goremote.itap.purdue.edu/Citrix/XenApp/auth/login.aspx) | GAMS can be accessed through ITAP software remote (https://goremote.itap.purdue.edu/Citrix/XenApp/auth/login.aspx) | ||
| − | variables | + | GAMS is a software that we can use to solve optimization problems. It is simple yet powerful software. |
| + | The following is a sample of how the code will look like on GAMS. The code before is trying to minimize the cost of a recycling company. There are methods to recycling and company wants to find the optimized way to operate. | ||
| + | |||
| + | We need to define our variables in this section | ||
| + | |||
| + | '''variables | ||
objval "objective function value" | objval "objective function value" | ||
x1 "new wood pulp" | x1 "new wood pulp" | ||
| Line 28: | Line 54: | ||
y2 "# of products produced by method 2" | y2 "# of products produced by method 2" | ||
y3 "# of products produced by method 3" | y3 "# of products produced by method 3" | ||
| − | y4 "# of products produced by method 4" | + | y4 "# of products produced by method 4"''' |
| − | free variables | + | We define the type of variables here |
| + | |||
| + | '''free variables | ||
objval; | objval; | ||
| Line 42: | Line 70: | ||
method_3 "produce from method 3" | method_3 "produce from method 3" | ||
rest_80 "process 1 has to bw lesser than or equal to 80" | rest_80 "process 1 has to bw lesser than or equal to 80" | ||
| − | atleast_100 "the # of products must be at least 100"; | + | atleast_100 "the # of products must be at least 100";''' |
| − | obj .. | + | This is where we code our objective function and constraints |
| + | |||
| + | '''obj .. | ||
objval =e= 100*x1+50*x2+20*x3; | objval =e= 100*x1+50*x2+20*x3; | ||
| Line 61: | Line 91: | ||
atleast_100 .. | atleast_100 .. | ||
| − | y1+y2+y3+y4 =g= 100; | + | y1+y2+y3+y4 =g= 100;''' |
| − | + | Since our goal is to minimize the cost, we use "lp minimizing" function to minimize our 'objval' | |
| − | + | '''model absmall /all/; | |
| − | + | solve absmall using lp minimizing objval;''' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
'''My experience with linear programing''' | '''My experience with linear programing''' | ||
| − | + | ---- | |
| − | I have learned linear programing from a class in school of industrial engineering, IE335 | + | I have learned linear programing from a class in school of industrial engineering, IE335. When the data is very big, for instance, calculations involving in traveling in the outer space, we need linear programing to help us break down huge problems to smaller problems. Linear programing and non-linear programming is still a very active area of research. We always want to find a quickest possible ways to optimize our operations. I found that linear programming is very useful and interesting. |
| − | + | ||
| − | + | ||
| − | + | ||
'''Courses for linear programing''' | '''Courses for linear programing''' | ||
| + | ---- | ||
| + | If you are interested more in Linear programing and would like to take a course. I have listed the courses that relates to Linear programming. | ||
| − | + | IE 335 - Operation Research - Optimization | |
| + | Introduction to deterministic optimization modeling and algorithms in operations research. Emphasis on formulation and solution of linear programs, networks flows, and integer programs. Typically offered Fall Spring. | ||
CS 51500 - Numerical Linear Algebra. (was CS 515: Numerical Analysis of Linear Systems till 2009) | CS 51500 - Numerical Linear Algebra. (was CS 515: Numerical Analysis of Linear Systems till 2009) | ||
| Line 97: | Line 121: | ||
'''Further studies''' | '''Further studies''' | ||
| − | + | ---- | |
If you are interested in reading about Linear programming this link will give you the list of textbooks you can look at. | If you are interested in reading about Linear programming this link will give you the list of textbooks you can look at. | ||
[https://engineering.purdue.edu/~engelb/abe565/lpbooks.html List of textbooks] | [https://engineering.purdue.edu/~engelb/abe565/lpbooks.html List of textbooks] | ||
| − | ---- | + | |
| + | |||
| + | Stapel, Elizabeth. "Linear Programming: Introduction." Purplemath. Available from | ||
| + | http://www.purplemath.com/modules/linprog.htm. Accessed 11 December 2011 | ||
| + | |||
| + | ----- | ||
Go back to previous page [[2011_Fall_MA_265_Walther]] | Go back to previous page [[2011_Fall_MA_265_Walther]] | ||
[[Category:MA265Fall2011Walther]] | [[Category:MA265Fall2011Walther]] | ||
Latest revision as of 08:14, 11 April 2013
Linear Programming
Student project for MA265
What is linear programing?
Linear programing is a mathematical method you can apply to find best possible results such as maximum profit or minimum cost. Linear programing practically use as one of the optimization problem solvers. In general, to solve a optimization problem, you need to have an objective (what do you want to solve? Do you want to maximize or minimize your function?) and constraints related to your function. Putting objective and constraints function together on a graph will generate a feasible region.
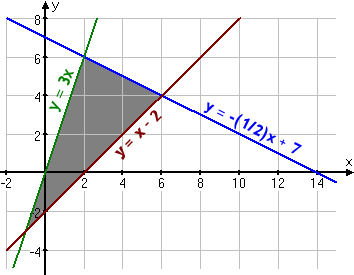
For example,
Objective function max -1/2x + 7
Constraints y=3x y=x-2
(source: http://www.purplemath.com/modules/linprog.htm)
The shade area is the feasible region
There are many software that help you solve optimization problems. In this page, I will focus on how to use GAMS.
GAMS
GAMS can be accessed through ITAP software remote (https://goremote.itap.purdue.edu/Citrix/XenApp/auth/login.aspx)
GAMS is a software that we can use to solve optimization problems. It is simple yet powerful software. The following is a sample of how the code will look like on GAMS. The code before is trying to minimize the cost of a recycling company. There are methods to recycling and company wants to find the optimized way to operate.
We need to define our variables in this section
variables objval "objective function value" x1 "new wood pulp" x2 "recycled office paper" x3 "recycled newsprint" y1 "# of products produced by method 1" y2 "# of products produced by method 2" y3 "# of products produced by method 3" y4 "# of products produced by method 4"
We define the type of variables here
free variables
objval;
positive variables
x1,x2,x3,y1,y2,y3,y4;
equations
obj "total cost" method_1 "produce from method 1" method_2 "produce from method 2" method_3 "produce from method 3" rest_80 "process 1 has to bw lesser than or equal to 80" atleast_100 "the # of products must be at least 100";
This is where we code our objective function and constraints
obj ..
objval =e= 100*x1+50*x2+20*x3;
method_1 ..
x1 =e= 3*y1+y2+y3;
method_2 ..
x2 =e= 4*y2+8*y4;
method_3 ..
x3 =e= 12*y3;
rest_80 ..
x1 =l= 80;
atleast_100 ..
y1+y2+y3+y4 =g= 100;
Since our goal is to minimize the cost, we use "lp minimizing" function to minimize our 'objval'
model absmall /all/;
solve absmall using lp minimizing objval;
My experience with linear programing
I have learned linear programing from a class in school of industrial engineering, IE335. When the data is very big, for instance, calculations involving in traveling in the outer space, we need linear programing to help us break down huge problems to smaller problems. Linear programing and non-linear programming is still a very active area of research. We always want to find a quickest possible ways to optimize our operations. I found that linear programming is very useful and interesting.
Courses for linear programing
If you are interested more in Linear programing and would like to take a course. I have listed the courses that relates to Linear programming.
IE 335 - Operation Research - Optimization Introduction to deterministic optimization modeling and algorithms in operations research. Emphasis on formulation and solution of linear programs, networks flows, and integer programs. Typically offered Fall Spring.
CS 51500 - Numerical Linear Algebra. (was CS 515: Numerical Analysis of Linear Systems till 2009) Computational aspects of linear algebra; linear equations and matrices, direct and iterative methods; eigenvalues and eigenvectors of matrices; error analysis.
ECE 580 - Optimization Methods for Systems and Control. Introduction to various methods of obtaining the extremum of a nondynamic or a dynamic system and their use in control system design. Linear programming, various search methods, nonlinear programming and dynamic programming. Various real-life applications are discussed, and appropriate case studies are investigated.
IE 535 - Linear Programming. Optimization of linear objective functions subject to linear constraints. Development of theory and algorithmic strategies for solving linear programming problems.
Further studies
If you are interested in reading about Linear programming this link will give you the list of textbooks you can look at.
Stapel, Elizabeth. "Linear Programming: Introduction." Purplemath. Available from
http://www.purplemath.com/modules/linprog.htm. Accessed 11 December 2011
Go back to previous page 2011_Fall_MA_265_Walther