| Line 95: | Line 95: | ||
e) Quantization artifacts in the dark area. | e) Quantization artifacts in the dark area. | ||
| + | ---- | ||
| + | ===Related Problem=== | ||
| + | Consider a color imaging device that takes input values of <math> (r,g,b) </math> and produces ouput <math> (X,Y,Z)</math> values given by | ||
| + | |||
| + | <math> | ||
| + | \left[ {\begin{array}{*{20}{c}} | ||
| + | X\\ | ||
| + | Y\\ | ||
| + | Z | ||
| + | \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} | ||
| + | a&b&c\\ | ||
| + | d&e&f\\ | ||
| + | g&h&i | ||
| + | \end{array}} \right]\left[ {\begin{array}{*{20}{c}} | ||
| + | r^\alpha\\ | ||
| + | g^\alpha\\ | ||
| + | b^\alpha | ||
| + | \end{array}} \right] | ||
| + | </math> | ||
| + | |||
| + | a) Calculate the white point of the device in chromaticity coordinates. | ||
| + | |||
| + | b) What are the primaries associated with the r,g, and b components respectively? | ||
| + | |||
| + | c) What is the gamma of the device? | ||
| + | |||
| + | d) Draw the region on the chromaticity diagram corresponding to <math> r < 0, g > 0, b > 0</math>. | ||
---- | ---- | ||
[[ECE_PhD_Qualifying_Exams|Back to ECE QE page]]: | [[ECE_PhD_Qualifying_Exams|Back to ECE QE page]]: | ||
Revision as of 06:17, 21 March 2013
Contents
ECE Ph.D. Qualifying Exam in Communication Networks Signal and Image processing (CS), Question 5, August 2012
- Problem 1 , 2
Problem 1
Consider the emissive display device which is accurately modeled by the equation
$ \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b&c\\ d&e&f\\ g&h&i \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R\\ G\\ B \end{array}} \right] $
where R, G and B are the red, green, and blue inputs in the range 0 to 255 that are used to modulate physically realizable color primaries.
a) What is the gamma of the device?
b) What are the chromaticity components $ (x_r,y_r), (x_g,y_g) $ and $ (x_b,y_b) $ of the device's three primaries.
c) What are the chromaticity components $ (x_w,y_w) $ of the device's white point.
d) If $ (X,Y,Z)=(0,1/2,1/2) $, then what can you say about the values of $ (R,G,B) $? (Hint: Draw a chromaticity diagram to find the answer.)
e) Imagine that the values of $ (R,G,B) $ are quantized to 8 bits, and that you view a smooth gradient from black to white on this device. What artifact are you likely to see, and where in the gradient will you see it?
Solution:
a) $ \gamma=1 $
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d)
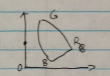
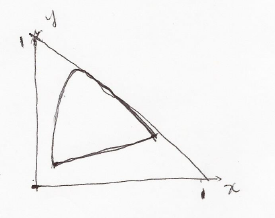
If $ (X,Y,Z)=(0,1/2,1/2) $, then $ (x,y)=(0,1/2) $.
In the chromaticity diagram, this point is outside the horse shoe shape, so its RGB values are not all larger than 0 ($ R<0,G>0,B>0 $).
e) We are likely to see quantization artifact in dark region.
Solution From Another Student:
a) The gamma is 1
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d) This color is imaginary. At least one of R,G,B values must be negative. Cannot be produced by this device.
The student can be more specific about the positive or negative of each R,G,B value of this color.
e) Quantization artifacts in the dark area.
Related Problem
Consider a color imaging device that takes input values of $ (r,g,b) $ and produces ouput $ (X,Y,Z) $ values given by
$ \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b&c\\ d&e&f\\ g&h&i \end{array}} \right]\left[ {\begin{array}{*{20}{c}} r^\alpha\\ g^\alpha\\ b^\alpha \end{array}} \right] $
a) Calculate the white point of the device in chromaticity coordinates.
b) What are the primaries associated with the r,g, and b components respectively?
c) What is the gamma of the device?
d) Draw the region on the chromaticity diagram corresponding to $ r < 0, g > 0, b > 0 $.