| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == Fun and Challenging Games Directly Related to Discrete Mathematics == | + | == Fun and Challenging Games Directly Related to [[MA375|Discrete Mathematics]] == |
'''For interactive games''' relating to our Discrete Mathematics class, check out these games that may help in understanding some of the chapters within our book, coming from our book, Discrete Mathematics and Its Applications: See [http://highered.mcgraw-hill.com/sites/0073383090/student_view0/interactive_demonstration_applets.html# Interactive Demonstration Applets] for more games. | '''For interactive games''' relating to our Discrete Mathematics class, check out these games that may help in understanding some of the chapters within our book, coming from our book, Discrete Mathematics and Its Applications: See [http://highered.mcgraw-hill.com/sites/0073383090/student_view0/interactive_demonstration_applets.html# Interactive Demonstration Applets] for more games. | ||
| Line 19: | Line 19: | ||
The answer may be surprising since one may think by using your intuition that the chance is 50-50 since you think there is an equal chance a car is behind each door. However, this is not the case. You should always change and pick the final door since the chances are 2 in 3 there is a car behind that door. There are at least two ways to show this: | The answer may be surprising since one may think by using your intuition that the chance is 50-50 since you think there is an equal chance a car is behind each door. However, this is not the case. You should always change and pick the final door since the chances are 2 in 3 there is a car behind that door. There are at least two ways to show this: | ||
| − | First, let the doors be called X,Y, and Z. Let Cx be the | + | First, let the doors be called X,Y, and Z. Let Cx, Cy, Cz be the events that the car is behind door X, Y, Z respectively. Let Dx, Dy, Dz be the events that the host opens door X, Y, Z respectively. Choosing door X, the possibility you win a car if you switch the choice is given by the formula: |
P(Dz ^ Cy) + P(Dy ^ Cz) | P(Dz ^ Cy) + P(Dy ^ Cz) | ||
| − | = P(Cy)*P( | + | = P(Cy)*P(Dz|Cy) + P(Cz)*(P(Dy|Cz) |
= (1/3 * 1) + (1/3 * 1) | = (1/3 * 1) + (1/3 * 1) | ||
| Line 65: | Line 65: | ||
''Question:'' | ''Question:'' | ||
| + | |||
A true-false question is to be posted to a husband and wife team on a quiz game show. Both the husband and wife will independently give the correct answer with probability p. Which of the following is a better strategy? | A true-false question is to be posted to a husband and wife team on a quiz game show. Both the husband and wife will independently give the correct answer with probability p. Which of the following is a better strategy? | ||
a) Choose one of them and let the person answer the question. | a) Choose one of them and let the person answer the question. | ||
| Line 73: | Line 74: | ||
''Answer:'' | ''Answer:'' | ||
| + | |||
Using this table (Table 1): | Using this table (Table 1): | ||
| + | When Man and Woman both answer correctly: p^2 | ||
| − | + | When Man answers correctly and Woman answers incorrectly: (1-p)p | |
| − | + | ||
| − | + | When Man answers correctly and Woman answers incorrectly: p(1-p) | |
| + | |||
| + | When Man and Woman both answer incorrectly: (1-p)^2 | ||
Table 1: The possible probabilities of agreement for the couple in the following problem. When asked a question, four possible outcomes can occur corresponding to the correctness of the mans (woman’s) answer. First row represents to the times when the husband answers the question correctly, the second row to the times when the husband answers the question incorrectly. In the same way, the first column corresponds to the times when the wife is correct and second column to the times when the wife is incorrect. | Table 1: The possible probabilities of agreement for the couple in the following problem. When asked a question, four possible outcomes can occur corresponding to the correctness of the mans (woman’s) answer. First row represents to the times when the husband answers the question correctly, the second row to the times when the husband answers the question incorrectly. In the same way, the first column corresponds to the times when the wife is correct and second column to the times when the wife is incorrect. | ||
| Line 95: | Line 100: | ||
where in computing this result we have used the joint probabilities found in Table 1 to evaluate terms like P(Cm,Cwc). Note that this result is the same as in Part (a) of this problem showing that there is no benefit to using this strategy. | where in computing this result we have used the joint probabilities found in Table 1 to evaluate terms like P(Cm,Cwc). Note that this result is the same as in Part (a) of this problem showing that there is no benefit to using this strategy. | ||
| − | |||
'''''CHALLENGE:''''' | '''''CHALLENGE:''''' | ||
| + | |||
Please post responses if you think of any way to have a winning strategy for either player. | Please post responses if you think of any way to have a winning strategy for either player. | ||
A fun and interesting game Professor Walther discussed is figuring out the best strategy to eat a chocolate bar given the certain circumstances: | A fun and interesting game Professor Walther discussed is figuring out the best strategy to eat a chocolate bar given the certain circumstances: | ||
| Line 131: | Line 136: | ||
Thanks - Carolyn --[[User:Chanes|Chanes]] 19:45, 2 February 2012 (UTC) | Thanks - Carolyn --[[User:Chanes|Chanes]] 19:45, 2 February 2012 (UTC) | ||
| + | Here are some funny images relating to math I thought everyone would enjoy as well! :) | ||
| + | |||
| + | [[Image:Whale.jpg]] | ||
| + | |||
| + | [[Image:images1.jpg]] | ||
| + | |||
| + | [[Image:images2.jpg]] | ||
| + | |||
| + | [[Image:images5.jpg]] | ||
| + | |||
| + | [[Image:JamesBond.jpg]] | ||
| + | |||
| + | Images obtained using Google: [http://www.google.com/search?hl=en&safe=off&client=safari&rls=en&biw=1099&bih=626&tbm=isch&sa=1&q=failing+math&oq=failing+math&aq=f&aqi=g1g-S8g-mS1&aql=&gs_l=img.3..0j0i24l8j0i5i24.596471.597174.0.597590.6.6.0.0.0.0.115.534.4j2.6.0...0.0.S5ABYSU-iuM] | ||
| + | |||
| + | |||
| + | ---- | ||
--- | --- | ||
| Line 140: | Line 161: | ||
My aim is to solve at least one problem per week, starting tomorrow 23 January. This pace will certainly slow down as the difficult of the problem increases, and for anyone who wants to play the game together, please let me know at lee832 at purdue dot edu | My aim is to solve at least one problem per week, starting tomorrow 23 January. This pace will certainly slow down as the difficult of the problem increases, and for anyone who wants to play the game together, please let me know at lee832 at purdue dot edu | ||
| − | + | ---- | |
| + | [[2012_Spring_MA_375_Walther|Back to MA375, Spring 2012, Prof. Walther]] | ||
[[Category:MA375Spring2010Walther]] | [[Category:MA375Spring2010Walther]] | ||
| + | [[Category:bonus point project]] | ||
| + | [[Category:MA375]] | ||
| + | [[Category:math]] | ||
| + | [[Category:discrete math]] | ||
| + | [[Category:probability]] | ||
Latest revision as of 06:52, 21 March 2013
Contents
[hide]Fun and Challenging Games Directly Related to Discrete Mathematics
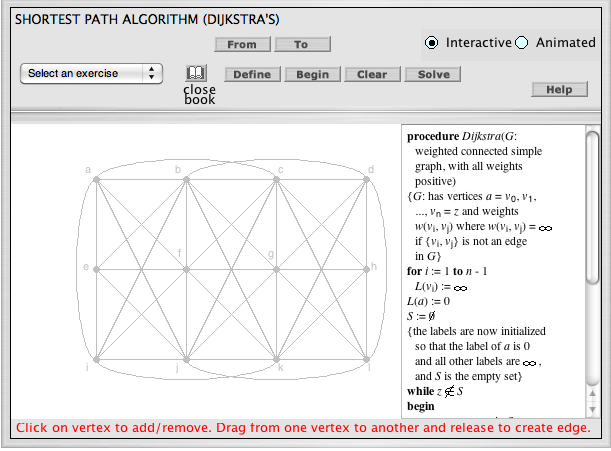
For interactive games relating to our Discrete Mathematics class, check out these games that may help in understanding some of the chapters within our book, coming from our book, Discrete Mathematics and Its Applications: See Interactive Demonstration Applets for more games. For example: In Chapter 10, we see the below picture helps demonstrate concepts involving the Shortest Path Algorithm (Dijkstra's).
There are a variety of interactive games for Chapters 1,3,8,10, and 11 to help learn different discrete mathematics concepts while playing these interactive games!
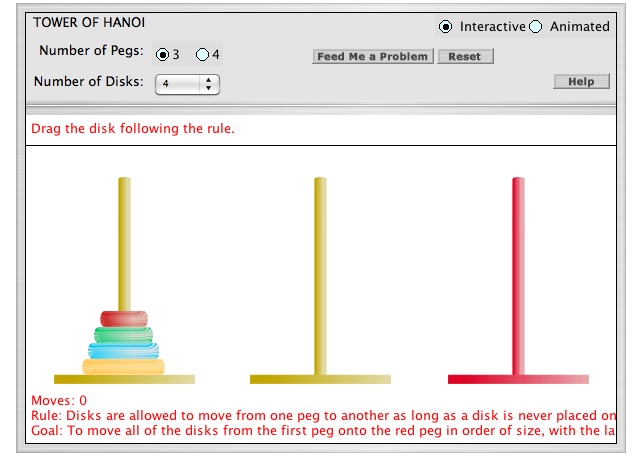
Relating one of the games available on this website to our class lectures, we discussed how to figure out the Tower of Hanoi. If you would like to refer to our notes, this lecture was on February 16th, 2012. As a refresher, the goal is to get all the washers on the last peg, but we are only allowed to move one peg at a time. Try playing this game in order to figure out the minimum number of moves. Doing this mathematically without randomly guessing, try letting An equal the minimal number of moves needed where n equals the number of washers. Follow this website to see this game with either 3 or 4 pegs and to play more games as well! Tower of Hanoi
The Monty Hall Problem
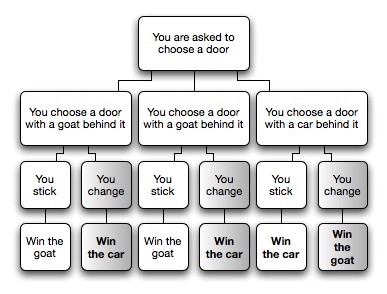
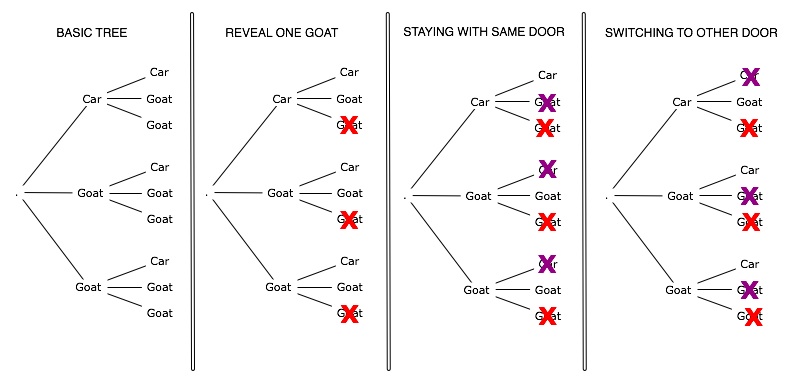
Another fact about probability and games, brings me to think about a very popular problem called The Monty Hall Problem. The basis of this problem is this: You are on a television game show where the idea is to win a car as the final prize. The host of the game show has three doors for you to pick from. You have the opportunity to win a car behind one of the doors and goats behind the other two doors. The host asks you to choose a door. Then once you pick the door, it is not opened right away. One of the doors you didn't choose is opened to reveal a goat, since the host knows what is behind each one of the doors. You are given the chance to change your mind before the doors are opened and you either get the car or the goat. So the host asks you if you want to change your mind and pick the other door instead. What should you do?
The answer may be surprising since one may think by using your intuition that the chance is 50-50 since you think there is an equal chance a car is behind each door. However, this is not the case. You should always change and pick the final door since the chances are 2 in 3 there is a car behind that door. There are at least two ways to show this: First, let the doors be called X,Y, and Z. Let Cx, Cy, Cz be the events that the car is behind door X, Y, Z respectively. Let Dx, Dy, Dz be the events that the host opens door X, Y, Z respectively. Choosing door X, the possibility you win a car if you switch the choice is given by the formula:
P(Dz ^ Cy) + P(Dy ^ Cz)
= P(Cy)*P(Dz|Cy) + P(Cz)*(P(Dy|Cz)
= (1/3 * 1) + (1/3 * 1)
= 2/3.
Second way is to work it out by drawing a picture. To help clarify this idea, let this picture below help illustrate this.
Images from Google Images.
In addition to computer interactive games, there are other ways to work our brains. An article from the publishers of the book we use in class, McGraw-Hill, points out the common mistakes made in Discrete Mathematics. The article starts out saying, In this section of the Guide we list many common mistakes that people studying discrete mathematics sometimes make. The list is organized chapter by chapter, based on when they first occur, but sometimes mistakes made early in the course perpetuate in later chapters. Also, some of these mistakes are remnants of misconceptions from high school mathematics (such as the impulse to assume that every operation distributes over every other operation). In most cases we describe the mistake, give a concrete example, and then offer advice about how to avoid it. To continue reading and working the brain to figure out why these mistakes occur, the link is: Common Mistakes in Discrete Mathematics. A few examples of the common mistakes usually made are listed:
• Overusing the term “by definition” in justifying statements in a proof. For example, Franklin Roosevelt was not the President of the United States at the start of the country’s entry into World War II in December, 1941, “by definition”; he was the President because he had been inaugurated as such early in 1941 and had not died or left office.
• Incorrectly starting a proof by assuming what is to be proved. A common occurrence of this in an earlier course is trying to prove trigonometric identities by starting with the identity and using algebra to reach A = A; this is not valid. Similarly, if we are trying to prove a set identity in Chapter 2, such as A ⊆ A ∪ B , it would be invalid to start with the statement A ⊆ A ∪ B .
• Failing to change the variable in a power series when necessary. For example, if a power series has xk−1 and you need it to be xk , you can replace k by k + 1 throughout the summation (including the limits) and simplify algebraically: ∞k=1 k xk−1 = ∞k+1=1(k + 1) x(k+1)−1 = ∞k=0(k + 1) xk .
On a different note, for those of you who believe tests or checking your knowledge are fun, there are multiple self-assessment quizzes available to you from Discrete Mathematics and Its Applications Seventh Edition - Kenneth H. Rosen: See Self-Assessments to get started now.
Slightly Easier Games:
For those of you majoring in Mathematics Education or would just like slightly easier games, here is a website which contains games for students all the way from kindergarden to eight grade. Math Playground Games For middle school and high school students, try this site for games. HotMath Games
An interesting article I found while researching was called Odds on: the maths behind game shows published by ABC Science. This article discusses how mathematics could be used on everyday game shows to put the odds of winning closer to your favor. Although it is an opinion piece, which quotes Simon Singh, about how math strategies are better than your chance instincts it shows different ways to better win prizes on game shows by switching to his methods. Game shows such as Deal or No Deal and Let's Make a Deal which were popular and are popular shows on television today are discussed.
Also, sticking with the same game show theme, John A. Rock wrote an article called Mathematics Behind Game Shows: The Best Way to Play in May 2008. There are many problems for practice involving all types of mathematics, focusing on probability mostly. The author makes the problems fun by using well known subjects in the problems; for example, The Price is Right, Jeopardy, Dodgeball, Find the Fake, Coin Flip, etc.' These problems can be done by anyone for fun on your own or in group activities in a classroom. If interested in this, be sure to see The Monty Hall Problem above.
Game Show Strategies Problem
Question:
A true-false question is to be posted to a husband and wife team on a quiz game show. Both the husband and wife will independently give the correct answer with probability p. Which of the following is a better strategy? a) Choose one of them and let the person answer the question. b) Have them both consider the question, and give common answer if they agree, or if they disagree, flip a coin to figure out which answer to give. - Problem taken from A First Course in Probability By: Sheldon Ross
Try yourself for practice/fun! If not, the answer is provided below.
Answer:
Using this table (Table 1): When Man and Woman both answer correctly: p^2
When Man answers correctly and Woman answers incorrectly: (1-p)p
When Man answers correctly and Woman answers incorrectly: p(1-p)
When Man and Woman both answer incorrectly: (1-p)^2
Table 1: The possible probabilities of agreement for the couple in the following problem. When asked a question, four possible outcomes can occur corresponding to the correctness of the mans (woman’s) answer. First row represents to the times when the husband answers the question correctly, the second row to the times when the husband answers the question incorrectly. In the same way, the first column corresponds to the times when the wife is correct and second column to the times when the wife is incorrect.
Part (a): Since each person has probability p of getting the correct answer, either one selected to represent the couple will answer correctly with probability p.
Part (b): To compute the probability that the couple answers correctly under this strategy we will condition our probability on the “agreement” matrix in Table 1 (the possible combinations of outcomes the couple may encounter when asked a question that they both answer). Define E as the event that the couple answers correctly, and let Cm (Cw) be the events that the man (women) answers the question correctly. We find that:
P(E) = P(E|Cm,Cw)P(Cm,Cw)+P(E|Cm,Cwc)P(Cm,Cwc) + P(E|Cmc ,Cw)P(Cmc ,Cw)+P(E|Cmc ,Cwc)P(Cmc ,Cwc). Now P(E|Cmc ,Cwc) = 0 since both the man and the woman agree but they both answer the question incorrectly. In that case the couple would return the incorrect answer to the question. In the same way we have that P(E|Cm,Cw) = 1.
Following the strategy of flipping a coin when the couple answers disagree we note that P(E|Cm,Cwc ) = P(E|Cmc ,Cw) = 1/2, so that the above probability when using this strategy becomes P(E)=1·p2 +1p(1−p)+1(1−p)p=p, 22 where in computing this result we have used the joint probabilities found in Table 1 to evaluate terms like P(Cm,Cwc). Note that this result is the same as in Part (a) of this problem showing that there is no benefit to using this strategy.
CHALLENGE:
Please post responses if you think of any way to have a winning strategy for either player. A fun and interesting game Professor Walther discussed is figuring out the best strategy to eat a chocolate bar given the certain circumstances: There are two players in this game, players A and B. They are given a bar of chocolate and both players are eating this bar. With player A taking a turn first, each player is to take turns eating chocolate. But, once a player chooses a piece of the chocolate, they must eat that piece plus all the other pieces that are not above it and also not to its left. Is there a winning strategy, and if so, which one would win and how?
If there are any requests for certain types of games or anything else, please let me know! Thanks, Carolyn Hanes
Opportunities Involving Math Games/Activities
Also, if anyone is interested in a fun math event to help out with then this event is for you! The Math Counts Competition is coming to Purdue and they are looking for some volunteers. Here is some information about what Math Counts is and how to get involved:
On Saturday, February 11, Purdue will be hosting the MathCOUNTS Regional competition here at Purdue University, and we are looking for volunteers to help out with the event. MathCOUNTS is a national middle school competition for students who excel in mathematics. MATHCOUNTS emphasizes fun and excitement through its signature competition program, which is entering its 29th year. Since 1983, over 6 million students have participated in MATHCOUNTS, and compiled data indicates that there is a strong correlation between participation and higher SAT scores, selection of STEM majors in college, and selection of STEM careers after college. The regional competition is a fun day where some of the brightest mathematics students in the region/state get to compete for a place in the national competition.
Volunteers will be needed from 8am to about 1pm. A volunteer can work all or a portion of the time. Their basic duties could include: helping with set-up and check-in, helping administer the tests; or help scoring the tests. Here is the schedule for the day. Volunteers will receive a free lunch and are invited to stay for the afternoon countdown round and awards. 8:30 a.m. Registration 9:00 Welcome and Introductions (10 min.) 9:10 Sprint Round (40 min.) 9:50 Break (15 min.) 10:05 Target Round (45 min.) 10:50 Break (10-15 min.) 11:00 Team Round (20 min.) 11:30 Lunch (provided - 1.5 hour) 1:00 p.m. Count Down (1 hour) in Class of 1950 Building Lecture Hall 2:00 Awards (following countdown)
Anyone who is interested in volunteering or has questions can contact Jerry Woodwar (jwoodwar@purdue.edu) or Vince Drnevich (drnevich@purdue.edu), Professor Emeritus, Civil Engineering, Purdue University.
The Math Club here at Purdue has speakers come and give talks about interesting topics related to Mathematics, check them out as well. Don't forget to participate in Project Euler if interested, which is the game posted below that was added! Thanks - Carolyn --Chanes 19:45, 2 February 2012 (UTC)
Here are some funny images relating to math I thought everyone would enjoy as well! :)
Images obtained using Google: [1]
---
Thanks for sharing info Carolyn.
I only want to add a little "game" I am beginning to play this semester- Project Euler. It is a small project initiated by Colin Hughes in which he and his peers posted mathematical challenges of all level, from novice (e.g. Problem 1:"Add all the natural numbers below one thousand that are multiples of 3 or 5." to extremely difficult (Problem 368: Kepmner Like Series).
What is interesting about project Euler is that it is like an Massive Multiplayer Online gaming experience for incredibly nerdy types (me, included)- you create an account, level up by solving more and more problems, score achievements, and share your answer to another user through problem-specific forums. Solving the problem alone is only marks the entrance to the Project Euler; the real challenge begins when you share your answer with other users to search for the most elegant (and therefore, beautiful) solution. For instance, I answered problem number 3 by writing a brute force program, thereby taking ~4-5 seconds to get my answer (any program that I write that takes more than a second to execute is an ill-written program). But I found another user who wrote a more efficient program that could do the same task in less than fraction of a second because he actually used his brain to recognize and craft a more efficient approach to the solution.
My aim is to solve at least one problem per week, starting tomorrow 23 January. This pace will certainly slow down as the difficult of the problem increases, and for anyone who wants to play the game together, please let me know at lee832 at purdue dot edu