(New page: == Sorting floating numbers == by Daniel Lee Last Edit: 27 January 2013 ---- '''Introduction''' It's well known that the comparison sorting algorithms have a theoretical lower bound of <m...) |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == Sorting floating numbers == | + | [[Category:tutorial]] |
| − | by Daniel Lee | + | [[Category:sort]] |
| − | + | ||
| + | == Sorting floating numbers == | ||
| + | |||
| + | by [[user:lee832|Daniel Lee]] | ||
| + | |||
---- | ---- | ||
| − | ''' | + | '''INTRODUCTION''' |
| − | It's well known that the comparison sorting algorithms have a theoretical lower bound of < | + | |
| + | During a CS251: Data Structure & Algorithms lecture about various sorting algorithms, Professor Aliaga mentioned a sorting algorithm of linear running time - radix sort. While showing us how radix sort can be used to sort binary numbers, he added that radix sort is not a general-purpose sorting algorithm, and our lower-bound for comparison sorts are still set at O(nlogn). But I wonder - all digital objects are represented as 0/1 in memory. Can I use radix sort to sort objects like floating point number whose binary structure is well defined? | ||
| + | |||
| + | <br> '''PRELIMINARIES''' | ||
| + | |||
| + | '''Radix Sort''' | ||
| + | |||
| + | It's well known that the comparison sorting algorithms have a theoretical lower bound of <span class="texhtml">''n''log''n''</span>. Therefore, we can have something radix sort, which fall outside the category of of comparison sort, that attains status of linear time sorting algorithm. To illustrate the maneuvers of radix sort, I first introduce bucket sort with an illustrative example: | ||
| + | <blockquote>Suppose you have a collection of marbles. You want to sort the marbles out categorically, say its color. You can easily sort out the marbles by going through each marble and placing them inside a "bucket" labeled blue, red, orange, yellow, etc, and Viola! your marbles are sorted. </blockquote> | ||
| + | I concede that the above example is incredibly simple, but it is only so because radix sort itself stems from a simple method. Now consider an example of radix sort: | ||
| + | <blockquote>Say you would like to sort 4 numbers, each represented by 4 binary digits: 0101 0111 1011 1000 We prepare two buckets, labeled "1" and "0" and do the following: </blockquote><blockquote> | ||
| + | '''1. Look at the 1st digit (count from the least significant) and throw the number into corresponding bucket''' | ||
| + | |||
| + | "0" = (1000) "1" = (0101, 0111, 1011) ''Note that the order in which the numbers are stored is of importance (I chose (-) instead of {-} or [-] to emphasize this)'' | ||
| + | |||
| + | '''2. Repeat 1 for kth digit from k = 1:4, maintaining its relative order. Elements in bucket "0" is given the lower ordering than the items in bucket "1".''' | ||
| + | |||
| + | '''k = 2: '''"0" = (1000, 0101) "1" = (0111, 1011) | ||
| + | |||
| + | '''k = 3: '''"0" = (1000, 1011) "1" = (0101, 0111) | ||
| + | |||
| + | '''k = 4:''' "0" = (0101, 0111) "1" = (1000, 1011) | ||
| + | |||
| + | '''3. Collect the elements, starting from bucket "0" and maintaining its relative order. Viola! The numbers are now sorted.''' | ||
| + | </blockquote> | ||
| + | Since it takes n*constant steps to categorize and throw each item into a bucket for each bit, the total time it takes to sort n number is given by n*constant *k where k = number of bits. Since k is usually 32 or 64 bits and therefore a constant, radix sort can sort n integers in O(n). | ||
| + | |||
| + | <br> | ||
| + | |||
| + | '''Floating Point Numbers''' | ||
| + | |||
| + | Integers can be represented as binary pretty readily (think two's complement), but how can we represent decimal numbers? Fixing the decimal point greatly limits the range and the precision of decimal point numbers we can represent. Hence the formulation of floating point numbers. Because floating point number is incredibly delicate and dangerous subject to touch upon, I leave the explanation to the experts- there are many articles written about floating point numbers [1][2], and I conclude my discussion with the following diagram from Professor Comer's textbook, Essentials of Computer Architecture[3]. The diagram outlines how floating point numbers are stored in memory. | ||
| + | |||
| + | [[Image:Comer.PNG]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | '''PROJECT OUTLINE''' | ||
| + | |||
| + | Since I know how floating point numbers are represented in memory, can I tweak general implementation of radix sort to sort floating point numbers? | ||
| + | |||
| + | '''Tasks''' | ||
| + | |||
| + | 1. Implement radix sort for integers (CHECK) | ||
| + | |||
| + | 2. Investigate how floating point is represented in memory and device a method to sort floating point numbers | ||
| + | |||
| + | 3. Implement modified radix sort for floating point numbers | ||
| + | |||
| + | 4. Naive analysis of running time? | ||
| + | |||
| + | '''RESULTS''' | ||
| + | |||
| + | '''Task 1: Building myFirstRadixSort.c''' | ||
| + | |||
| + | I elected to build a queue with linked list to implement bucket. My first attempt at radix sort takes in an array of short ints. Download the source code here (upload coming this weekend). Compile using the command: | ||
| + | <blockquote>>> make myFirstRadix.o </blockquote> | ||
| + | Input file should be a list of short ints, each number separated by a space. Simply run: | ||
| + | <blockquote>>> ./myfirstRadix < input.txt </blockquote> | ||
| + | The program will print out the sorted list. | ||
| + | |||
| + | '''Task 2: Manipulating floating-point number in memory''' | ||
| + | |||
| + | Since bit-wise operators that proved to be so useful in manipulating integer number is no longer in my toolkit (compiler treats bit-wise operator on floating point numbers as explicit compile-time error). Since I do not know much about compilers (yet), I needed to work with the C language to access the binary representation of floating point numbers in memory. | ||
| + | |||
| + | I defined a new data type called bitFloat as follows: | ||
| + | |||
| + | <br> | ||
| + | |||
| + | typdef union { | ||
| + | |||
| + | float num; | ||
| + | struct { | ||
| + | unsigned char lsb: 4; | ||
| + | unsigned char msb: 4; | ||
| + | } bit[4]; | ||
| + | |||
| + | } bitFloat; | ||
| + | |||
| + | |||
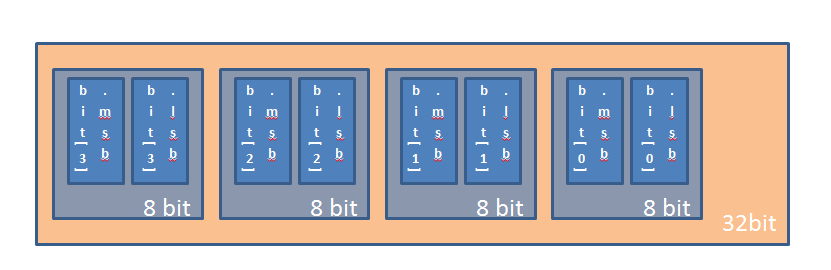
| + | "bitFloat" stores "float num", and its binary representation is stored in memory in the following way: | ||
| + | |||
| + | [[Image:FloatBit.PNG]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | And the following code | ||
| + | |||
| + | <br> | ||
| + | |||
| + | int main(void) { | ||
| + | bitFloat bF1, bF2; | ||
| + | bF1.num = 1; | ||
| + | bF2.num = -1; | ||
| + | printf("sign bit of %2.0f:\t%d\n", bF1.num, bF1.bit[3].msb >> 3); | ||
| + | printf("sign bit of %2.0f:\t%d\n", bF2.num, bF2.bit[3].msb >> 3); | ||
| + | } | ||
| + | |||
| + | produces | ||
| + | |||
| + | <br> | ||
| + | |||
| + | >> sign bit of 1: 0 | ||
| + | >> sign bit of -1: 1 | ||
| + | |||
| + | </br> | ||
| + | |||
| + | which is exactly what I sought after. | ||
| + | |||
| + | '''Task 3: Implement modified radix sort for floating point numbers ''' | ||
| + | |||
| + | My strategy reduces to three steps: | ||
| + | <blockquote> | ||
| + | |||
| + | 1. Do radix sort according to the binary value of each number's mantissa <br> | ||
| + | |||
| + | 2. Do radix sort according to the binary value of each number's exponent <br> | ||
| + | |||
| + | 3. Separate negative and positive numbers, and print accordingly | ||
| + | </blockquote> | ||
| + | To briefly explain what I mean by "print accordingly" in step 3, consider that <span class="texhtml">1000 > 100</span> while -1000 < -100. Then, if I define a function to print the positive numbers in a particular order, I need call the function in the reverse fashion for the negative numbers. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ''This project is taking too long! Will return later'' | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''REFERENCE''' | ||
| + | |||
| + | [1] Smith, Steven W. The Scientist and Engineer's Guide to Digital Signal Processing. <http://www.dspguide.com/ch4/3.htm> | ||
| + | |||
| + | [2] Schmalz, M.S. Organization of Computer Systems. http://www.cise.ufl.edu/~mssz/CompOrg/CDA-arith.html | ||
| + | |||
| + | [3] Comer, Douglas. Essentials of Computer Architecture. | ||
| + | |||
| + | Last Edit: 2 February 2013 | ||
| − | [[ | + | [[User:Lee832|back to Daniel Lee's Profile Page]] |
Latest revision as of 10:27, 18 March 2013
Sorting floating numbers
by Daniel Lee
INTRODUCTION
During a CS251: Data Structure & Algorithms lecture about various sorting algorithms, Professor Aliaga mentioned a sorting algorithm of linear running time - radix sort. While showing us how radix sort can be used to sort binary numbers, he added that radix sort is not a general-purpose sorting algorithm, and our lower-bound for comparison sorts are still set at O(nlogn). But I wonder - all digital objects are represented as 0/1 in memory. Can I use radix sort to sort objects like floating point number whose binary structure is well defined?
PRELIMINARIES
Radix Sort
It's well known that the comparison sorting algorithms have a theoretical lower bound of nlogn. Therefore, we can have something radix sort, which fall outside the category of of comparison sort, that attains status of linear time sorting algorithm. To illustrate the maneuvers of radix sort, I first introduce bucket sort with an illustrative example:
Suppose you have a collection of marbles. You want to sort the marbles out categorically, say its color. You can easily sort out the marbles by going through each marble and placing them inside a "bucket" labeled blue, red, orange, yellow, etc, and Viola! your marbles are sorted.
I concede that the above example is incredibly simple, but it is only so because radix sort itself stems from a simple method. Now consider an example of radix sort:
Say you would like to sort 4 numbers, each represented by 4 binary digits: 0101 0111 1011 1000 We prepare two buckets, labeled "1" and "0" and do the following:
1. Look at the 1st digit (count from the least significant) and throw the number into corresponding bucket
"0" = (1000) "1" = (0101, 0111, 1011) Note that the order in which the numbers are stored is of importance (I chose (-) instead of {-} or [-] to emphasize this)
2. Repeat 1 for kth digit from k = 1:4, maintaining its relative order. Elements in bucket "0" is given the lower ordering than the items in bucket "1".
k = 2: "0" = (1000, 0101) "1" = (0111, 1011)
k = 3: "0" = (1000, 1011) "1" = (0101, 0111)
k = 4: "0" = (0101, 0111) "1" = (1000, 1011)
3. Collect the elements, starting from bucket "0" and maintaining its relative order. Viola! The numbers are now sorted.
Since it takes n*constant steps to categorize and throw each item into a bucket for each bit, the total time it takes to sort n number is given by n*constant *k where k = number of bits. Since k is usually 32 or 64 bits and therefore a constant, radix sort can sort n integers in O(n).
Floating Point Numbers
Integers can be represented as binary pretty readily (think two's complement), but how can we represent decimal numbers? Fixing the decimal point greatly limits the range and the precision of decimal point numbers we can represent. Hence the formulation of floating point numbers. Because floating point number is incredibly delicate and dangerous subject to touch upon, I leave the explanation to the experts- there are many articles written about floating point numbers [1][2], and I conclude my discussion with the following diagram from Professor Comer's textbook, Essentials of Computer Architecture[3]. The diagram outlines how floating point numbers are stored in memory.
PROJECT OUTLINE
Since I know how floating point numbers are represented in memory, can I tweak general implementation of radix sort to sort floating point numbers?
Tasks
1. Implement radix sort for integers (CHECK)
2. Investigate how floating point is represented in memory and device a method to sort floating point numbers
3. Implement modified radix sort for floating point numbers
4. Naive analysis of running time?
RESULTS
Task 1: Building myFirstRadixSort.c
I elected to build a queue with linked list to implement bucket. My first attempt at radix sort takes in an array of short ints. Download the source code here (upload coming this weekend). Compile using the command:
>> make myFirstRadix.o
Input file should be a list of short ints, each number separated by a space. Simply run:
>> ./myfirstRadix < input.txt
The program will print out the sorted list.
Task 2: Manipulating floating-point number in memory
Since bit-wise operators that proved to be so useful in manipulating integer number is no longer in my toolkit (compiler treats bit-wise operator on floating point numbers as explicit compile-time error). Since I do not know much about compilers (yet), I needed to work with the C language to access the binary representation of floating point numbers in memory.
I defined a new data type called bitFloat as follows:
typdef union {
float num;
struct {
unsigned char lsb: 4;
unsigned char msb: 4;
} bit[4];
} bitFloat;
"bitFloat" stores "float num", and its binary representation is stored in memory in the following way:
And the following code
int main(void) {
bitFloat bF1, bF2;
bF1.num = 1;
bF2.num = -1;
printf("sign bit of %2.0f:\t%d\n", bF1.num, bF1.bit[3].msb >> 3);
printf("sign bit of %2.0f:\t%d\n", bF2.num, bF2.bit[3].msb >> 3);
}
produces
>> sign bit of 1: 0 >> sign bit of -1: 1
</br>
which is exactly what I sought after.
Task 3: Implement modified radix sort for floating point numbers
My strategy reduces to three steps:
1. Do radix sort according to the binary value of each number's mantissa
2. Do radix sort according to the binary value of each number's exponent
3. Separate negative and positive numbers, and print accordingly
To briefly explain what I mean by "print accordingly" in step 3, consider that 1000 > 100 while -1000 < -100. Then, if I define a function to print the positive numbers in a particular order, I need call the function in the reverse fashion for the negative numbers.
This project is taking too long! Will return later
REFERENCE
[1] Smith, Steven W. The Scientist and Engineer's Guide to Digital Signal Processing. <http://www.dspguide.com/ch4/3.htm>
[2] Schmalz, M.S. Organization of Computer Systems. http://www.cise.ufl.edu/~mssz/CompOrg/CDA-arith.html
[3] Comer, Douglas. Essentials of Computer Architecture.
Last Edit: 2 February 2013