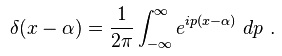| Line 1: | Line 1: | ||
[[Category:ECE301Spring2013JVK]] [[Category:ECE]] [[Category:ECE301]] [[Category:signalandsystems]] [[Category:problem solving]] | [[Category:ECE301Spring2013JVK]] [[Category:ECE]] [[Category:ECE301]] [[Category:signalandsystems]] [[Category:problem solving]] | ||
[[Category:Impulse Response]] | [[Category:Impulse Response]] | ||
| − | '''1.Impulse response''' | + | '''1.Impulse response'''<br> |
| − | Joseph Fourier first represented Fourier integral theorem in the following DOE: | + | Joseph Fourier first represented Fourier integral theorem in the following DOE:<br> |
[[Image:DOE1.jpg]][1] | [[Image:DOE1.jpg]][1] | ||
| − | Which is then introduced into the first delta function as following: | + | Which is then introduced into the first delta function as following:<br> |
[[Image:DOE2.jpg]][1] | [[Image:DOE2.jpg]][1] | ||
| − | And the end end up with what mathematicians called Dirac delta function: | + | And the end end up with what mathematicians called Dirac delta function:<br> |
[[Image:DOE3.jpg]] [1] | [[Image:DOE3.jpg]] [1] | ||
| Line 22: | Line 22: | ||
[[Image:n=100.jpg]] | [[Image:n=100.jpg]] | ||
[[Category:FFT]] | [[Category:FFT]] | ||
| + | <br> | ||
'''3.Filters''' | '''3.Filters''' | ||
Revision as of 10:29, 11 March 2013
1.Impulse response
Joseph Fourier first represented Fourier integral theorem in the following DOE:
![]() [1]
Which is then introduced into the first delta function as following:
[1]
Which is then introduced into the first delta function as following:
![]() [1]
And the end end up with what mathematicians called Dirac delta function:
[1]
And the end end up with what mathematicians called Dirac delta function:
The input x(t) is a function with a fundamental period x(t)= 1 from x= 0 to 1 and f(x)= -1 to 0, with a discontinuity at x=0. The following graphs from matlab represents Gibbs phenomena, as n increases the overshot decreases.
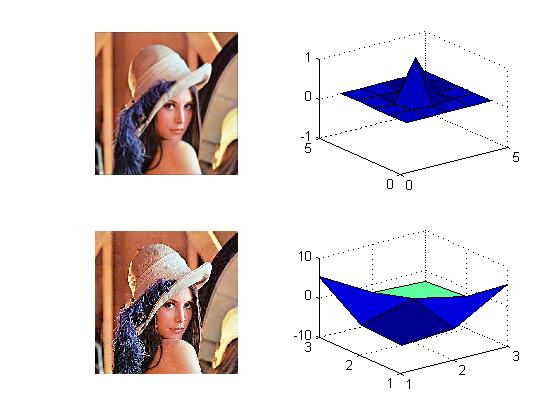
The upper is the Gaussian filter, while bottom is the unsharp.