m (Practice Question Mounty Hall ECE302S13Boutin moved to Practice Question Monty Hall ECE302S13Boutin: wrong spelling.) |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[ | + | <br> |
| + | |||
| + | = [[:Category:Problem solving|Practice Problem on]] Conditional Probability = | ||
| − | |||
---- | ---- | ||
| − | First, watch this video explaining the Mounty Hall Problem | + | |
| + | First, watch this video explaining the Mounty Hall Problem | ||
| + | |||
*<youtube>mhlc7peGlGg</youtube> | *<youtube>mhlc7peGlGg</youtube> | ||
| − | Then use the concept of conditional probability to explain why switching door leads to a probability of success equal to 2/3. | + | Then use the concept of conditional probability to explain why switching door leads to a probability of success equal to 2/3. |
| + | |||
---- | ---- | ||
| − | == Share your answers below == | + | == Share your answers below == |
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too! | You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too! | ||
| Line 15: | Line 19: | ||
---- | ---- | ||
| − | === Answer 1 === | + | === Answer 1 === |
| − | + | ||
| + | [[User:Green26|(alec green)]] | ||
| + | |||
| + | The Monty Hall problem outlined in the above video is analogous to our in-class 'Prisoner's Dilemma', where in the Monty Hall case: car = prisoner is released, goat = prisoner dies. | ||
| + | |||
| + | For the following explanation of this 'problem'/'dilemma', I assume two things: | ||
| + | |||
| + | . one door has car, other two doors have goats (three doors total) | ||
| + | . after the player selects his/her door, the game show host (GSH) will expose one door with a goat that the player has not chosen | ||
| + | |||
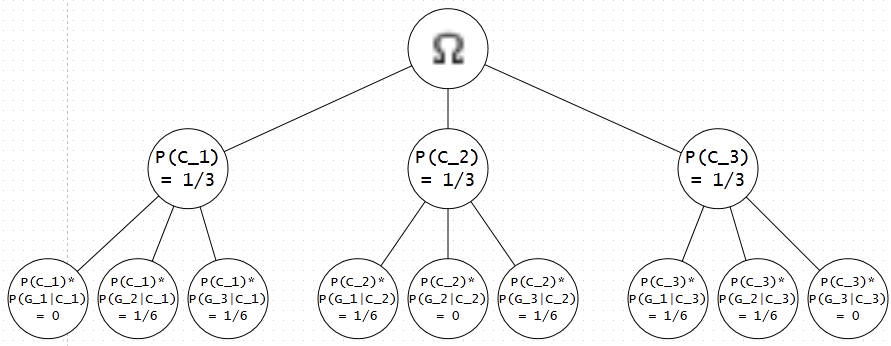
| + | Below you can see the event tree of cases, where 'C'=car and 'G'=goat. Note that all conditional probabilities of <math> P(G_i|C_i) \equiv 0</math> since the two events are mutually exclusive for the same door ''i''. | ||
| + | |||
| + | [[Image:Monty hall tree.PNG]] | ||
| + | |||
| + | '''Original Distribution of Probabilities''' | ||
| + | |||
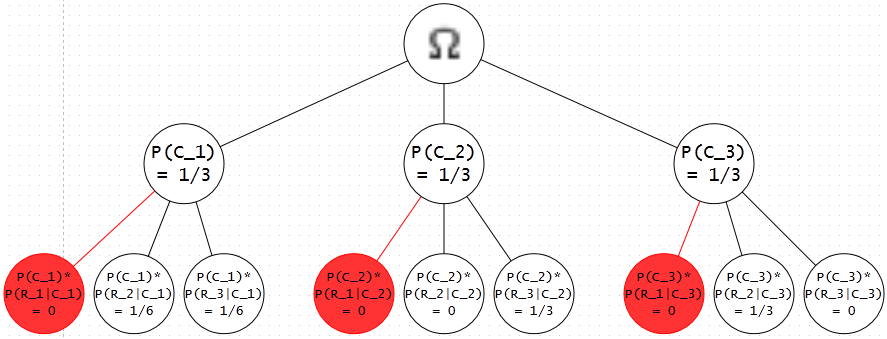
| + | Let's assume that we select door 1 in the hopes that a car sits behind it. Since the GSH is now limited to telling us which of the other two doors contain a goat, we can represent the probability of the GSH revealing ('R') which of the other two doors have a goat with a similar event tree (shown below). Note that sole the modification is that all <span class="texhtml">''P''(''G''<sub>1</sub> | ''C''<sub>''i''</sub>)</span> become <span class="texhtml">''P''(''R''<sub>1</sub> | ''C''<sub>''i''</sub>) = 0</span>. | ||
| + | |||
| + | [[Image:Monty hall tree mod.PNG]] | ||
| + | |||
| + | '''Modified Event Tree Representing the Probability GSH will 'R'eveal a Goat''' | ||
| + | |||
| + | Now, suppose the GSH reveals a goat behind door 3. This removes the possibility of door 3 having a car <span class="texhtml">(''P''(''C''<sub>3</sub>) = 0)</span>, so working backwards from the given event <span class="texhtml">''G''<sub>3</sub></span>, we can calculate the new probabilities of a car existing behind doors 1 and 2 via renormalization. We note that there are 3 possibilities that could have caused the GSH's revelation: | ||
| + | |||
| + | <math>P(R_3 \cap C_1) = P(C_1) \cdot P(R_3|C_1) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6} </math> | ||
| + | <math>P(R_3 \cap C_2) = P(C_2) \cdot P(R_3|C_2) = \frac{1}{3} \cdot 1 = \frac{1}{3} </math> | ||
| + | <math>P(R_3 \cap C_3) \equiv 0</math> | ||
| + | <math>\therefore P(C_1|R_3) = \frac{P(R_3 \cap C_1)}{P(R_3)} = \frac{\frac{1}{6}}{\frac{1}{6} + \frac{1}{3}} = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{3},</math> | ||
| + | <math>P(C_2|R_3) = \frac{P(R_3 \cap C_1)}{P(R_3)} = \frac{\frac{1}{3}}{\frac{1}{6} + \frac{1}{3}} = \frac{\frac{1}{3}}{\frac{1}{2}} = \frac{2}{3}</math> | ||
| + | |||
| + | Therefore, we observe that the probability of a car existing behind the door we originally chose remains the same (<math>\frac{1}{3}</math>) while the probability of the car existing behind the other unrevealed door has increased to <math>\frac{2}{3}</math>. We can generalize this to a 'Monty Hall Problem' with more than 3 doors: e.g., I determine the resultant probability spread for a 4-door scenario to be <math>\frac{1}{12}, \frac{1}{8},</math> and <math>\frac{1}{8}</math> 'normalized' as before to <math>\frac{1}{4}, \frac{3}{8},</math> and <math>\frac{3}{8}</math> respectively. | ||
| + | |||
| + | '''Intuitive Method for Solving this Problem''' | ||
| + | |||
| + | Because we know a goat must exist behind at least one of two doors that player did not choose (since at most one of the two goats can exist behind the chosen door), revealing where a single goat exists does not provide any more information to the chosen door's probability of hiding a car. So assuming door 1 is chosen as in the previous example: | ||
| + | |||
| + | <math>P_{initial}(C_1) = P_{final}(C_1) = \frac{1}{3}</math> | ||
| + | |||
| + | It's also evident that: | ||
| + | |||
| + | <math>P_{initial}(C_2) = P_{initial}(C_3) = \frac{1}{3}</math> | ||
| + | |||
| + | However, if door 3 is revealed to have a goat behind it as in the previous example: | ||
| + | |||
| + | <math>P_{final}(C_3) = P(C_3|G_3) \equiv 0</math> | ||
| + | |||
| + | By Axiom II: | ||
| + | |||
| + | <span class="texhtml">''P''<sub>''f''''i''''n''''a''''l''</sub>(''C''<sub>1</sub>) + ''P''<sub>''f''''i''''n''''a''''l''</sub>(''C''<sub>2</sub>) + ''P''<sub>''f''''i''''n''''a''''l''</sub>(''C''<sub>3</sub>) = ''P''<sub>''f''''i''''n''''a''''l''</sub>(Ω) = 1</span> | ||
| + | <math>\therefore 1 - P_{final}(C_1) = P_{final}(C_2) + P_{final}(C_3) = P_{final}(C_2) = \frac{2}{3}</math> | ||
| + | |||
---- | ---- | ||
| − | |||
| − | + | === Answer 2 === | |
| + | |||
| + | ''Answer Composed by [https://www.projectrhea.org/rhea/index.php/User:Lee832 Daniel Lee]'' | ||
| + | |||
| + | I attempt a laymen's solution to the Mounty Hall Problem. | ||
| + | |||
| + | We are given the following situation: | ||
| + | <blockquote> | ||
| + | ''Behind the doors ''A''<sub>1</sub>,''A''<sub>2</sub>,''A''<sub>3</sub> lie either a car or a goat; only one of the door hides behind it a car. You can choose one door and receive what is behind it. You want the car (important assumption). You've randomly select the door ''A''<sub></sub>''i''. Instead of opening the door ''A''<sub></sub>''i'', the '''host''', who knows which door hides the car, opens one of the other two doors ''you did not select'', say ''A''<sub></sub>''j'', revealing a nice fat goat behind it. Now, the host gives you an option to switch your door,''A''<sub></sub>''i'', with the other remaining door, ''A''<sub></sub>''k''. Should you switch your door?'' | ||
| + | </blockquote> | ||
| + | Intuition tells me that the switch should not matter, for the probability of choosing the door with a car is 1/3 regardless of what the host did. Right? | ||
| + | |||
| + | It is instructive to look at the situation from the host's perspective. Let's divide the situation in two cases. | ||
| + | |||
| + | <blockquote> | ||
| + | '''Case 1''': The door <span class="texhtml">''A''<sub>''i''</sub></span> hides behind it a car. | ||
| + | <br> | ||
| + | Then the doors <math>A_j, A_k</math> hides behind them bit fat goats. As a host, you simply pick one of the the remaining doors and reveal a nice fat goat behind it. In this case, if you do decide to switch, then you do not win the car. | ||
| + | <br><br> | ||
| + | '''Case 2''': The door <math>A_i</math> has a goat behind it. | ||
| + | <br> | ||
| + | Then either door <math>A_j</math> or <math>A_k</math> hides a car behind it. Let's say the door <math>A_j</math> has the car. In this case, you as a host have only one option: open door <math>A_k</math> and reveal the nice fat goat behind it. In this case, when you make the switch, you win the car. | ||
| + | </blockquote> | ||
| + | |||
| + | In summary: for case 1, if you make the switch you loose. In case 2, if you make the switch you win. | ||
| + | |||
| + | So the question of "switching" reduces to the following: what is our probability of case 1 and 2? This is simple. The probability of case 1 is the same as the probability of picking the door with a car, 1/3. The probability of case 2 is the same as the probability of picking a door with a goat, 2/3. Therefore, switching the door leads to the probability of success to 2/3. | ||
| + | |||
| + | In reflection, the probability of choosing the door with a car is 1/3 regardless of what the host did (I mean, he does it AFTER you've chosen your door). But the probability of the host choosing the door to reveal is dependent on your choice. And this makes the difference here. | ||
| + | |||
---- | ---- | ||
| − | === Answer 3 === | + | === Answer 3 === |
| − | Write it here. | + | |
| + | Write it here. | ||
---- | ---- | ||
| Line 30: | Line 113: | ||
[[2013 Spring ECE 302 Boutin|Back to ECE302 Spring 2013 Prof. Boutin]] | [[2013 Spring ECE 302 Boutin|Back to ECE302 Spring 2013 Prof. Boutin]] | ||
| − | [[ECE302|Back to ECE302]] | + | [[ECE302|Back to ECE302]] |
| + | |||
| + | [[Category:ECE302]] [[Category:ECE302Spring2013Boutin]] [[Category:Problem_solving]] [[Category:Probability]] | ||
Latest revision as of 12:49, 13 February 2013
Contents
Practice Problem on Conditional Probability
First, watch this video explaining the Mounty Hall Problem
Then use the concept of conditional probability to explain why switching door leads to a probability of success equal to 2/3.
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
The Monty Hall problem outlined in the above video is analogous to our in-class 'Prisoner's Dilemma', where in the Monty Hall case: car = prisoner is released, goat = prisoner dies.
For the following explanation of this 'problem'/'dilemma', I assume two things:
. one door has car, other two doors have goats (three doors total) . after the player selects his/her door, the game show host (GSH) will expose one door with a goat that the player has not chosen
Below you can see the event tree of cases, where 'C'=car and 'G'=goat. Note that all conditional probabilities of $ P(G_i|C_i) \equiv 0 $ since the two events are mutually exclusive for the same door i.
Original Distribution of Probabilities
Let's assume that we select door 1 in the hopes that a car sits behind it. Since the GSH is now limited to telling us which of the other two doors contain a goat, we can represent the probability of the GSH revealing ('R') which of the other two doors have a goat with a similar event tree (shown below). Note that sole the modification is that all P(G1 | Ci) become P(R1 | Ci) = 0.
Modified Event Tree Representing the Probability GSH will 'R'eveal a Goat
Now, suppose the GSH reveals a goat behind door 3. This removes the possibility of door 3 having a car (P(C3) = 0), so working backwards from the given event G3, we can calculate the new probabilities of a car existing behind doors 1 and 2 via renormalization. We note that there are 3 possibilities that could have caused the GSH's revelation:
$ P(R_3 \cap C_1) = P(C_1) \cdot P(R_3|C_1) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6} $ $ P(R_3 \cap C_2) = P(C_2) \cdot P(R_3|C_2) = \frac{1}{3} \cdot 1 = \frac{1}{3} $ $ P(R_3 \cap C_3) \equiv 0 $ $ \therefore P(C_1|R_3) = \frac{P(R_3 \cap C_1)}{P(R_3)} = \frac{\frac{1}{6}}{\frac{1}{6} + \frac{1}{3}} = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{3}, $ $ P(C_2|R_3) = \frac{P(R_3 \cap C_1)}{P(R_3)} = \frac{\frac{1}{3}}{\frac{1}{6} + \frac{1}{3}} = \frac{\frac{1}{3}}{\frac{1}{2}} = \frac{2}{3} $
Therefore, we observe that the probability of a car existing behind the door we originally chose remains the same ($ \frac{1}{3} $) while the probability of the car existing behind the other unrevealed door has increased to $ \frac{2}{3} $. We can generalize this to a 'Monty Hall Problem' with more than 3 doors: e.g., I determine the resultant probability spread for a 4-door scenario to be $ \frac{1}{12}, \frac{1}{8}, $ and $ \frac{1}{8} $ 'normalized' as before to $ \frac{1}{4}, \frac{3}{8}, $ and $ \frac{3}{8} $ respectively.
Intuitive Method for Solving this Problem
Because we know a goat must exist behind at least one of two doors that player did not choose (since at most one of the two goats can exist behind the chosen door), revealing where a single goat exists does not provide any more information to the chosen door's probability of hiding a car. So assuming door 1 is chosen as in the previous example:
$ P_{initial}(C_1) = P_{final}(C_1) = \frac{1}{3} $
It's also evident that:
$ P_{initial}(C_2) = P_{initial}(C_3) = \frac{1}{3} $
However, if door 3 is revealed to have a goat behind it as in the previous example:
$ P_{final}(C_3) = P(C_3|G_3) \equiv 0 $
By Axiom II:
Pf'i'n'a'l(C1) + Pf'i'n'a'l(C2) + Pf'i'n'a'l(C3) = Pf'i'n'a'l(Ω) = 1 $ \therefore 1 - P_{final}(C_1) = P_{final}(C_2) + P_{final}(C_3) = P_{final}(C_2) = \frac{2}{3} $
Answer 2
Answer Composed by Daniel Lee
I attempt a laymen's solution to the Mounty Hall Problem.
We are given the following situation:
Behind the doors A1,A2,A3 lie either a car or a goat; only one of the door hides behind it a car. You can choose one door and receive what is behind it. You want the car (important assumption). You've randomly select the door Ai. Instead of opening the door Ai, the host, who knows which door hides the car, opens one of the other two doors you did not select, say Aj, revealing a nice fat goat behind it. Now, the host gives you an option to switch your door,Ai, with the other remaining door, Ak. Should you switch your door?
Intuition tells me that the switch should not matter, for the probability of choosing the door with a car is 1/3 regardless of what the host did. Right?
It is instructive to look at the situation from the host's perspective. Let's divide the situation in two cases.
Case 1: The door Ai hides behind it a car.
Then the doors $ A_j, A_k $ hides behind them bit fat goats. As a host, you simply pick one of the the remaining doors and reveal a nice fat goat behind it. In this case, if you do decide to switch, then you do not win the car.
Case 2: The door $ A_i $ has a goat behind it.
Then either door $ A_j $ or $ A_k $ hides a car behind it. Let's say the door $ A_j $ has the car. In this case, you as a host have only one option: open door $ A_k $ and reveal the nice fat goat behind it. In this case, when you make the switch, you win the car.
In summary: for case 1, if you make the switch you loose. In case 2, if you make the switch you win.
So the question of "switching" reduces to the following: what is our probability of case 1 and 2? This is simple. The probability of case 1 is the same as the probability of picking the door with a car, 1/3. The probability of case 2 is the same as the probability of picking a door with a goat, 2/3. Therefore, switching the door leads to the probability of success to 2/3.
In reflection, the probability of choosing the door with a car is 1/3 regardless of what the host did (I mean, he does it AFTER you've chosen your door). But the probability of the host choosing the door to reveal is dependent on your choice. And this makes the difference here.
Answer 3
Write it here.