| Line 25: | Line 25: | ||
<span style="color:red">Instructor's note: This is really the second answer presented. It would be better if we could keep the first answer "as is", and put the correction as a second answer. Mistakes are nothing to be ashamed of! Making mistakes makes you learn! -pm</span> | <span style="color:red">Instructor's note: This is really the second answer presented. It would be better if we could keep the first answer "as is", and put the correction as a second answer. Mistakes are nothing to be ashamed of! Making mistakes makes you learn! -pm</span> | ||
| + | [[User:Green26|(alec green)]] | ||
All elements in the following union are distinct, therefore the union is a set. | All elements in the following union are distinct, therefore the union is a set. | ||
Latest revision as of 12:48, 13 February 2013
Contents
Practice Problem on set operations
Consider the following sets:
$ \begin{align} S_1 &= \left\{ \frac{1}{2}, 1, 1.4, 2 \right\}, \\ S_2 & = \left\{ 0.\bar{9}, 1.40, \frac{42}{21}, 17\right\}. \\ \end{align} $
Write $ S_1 \cup S_2 $ explicitely. Is $ S_1 \cup S_2 $ a set?
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
Instructor's note: This is really the second answer presented. It would be better if we could keep the first answer "as is", and put the correction as a second answer. Mistakes are nothing to be ashamed of! Making mistakes makes you learn! -pm
All elements in the following union are distinct, therefore the union is a set.
$ S_1 \cup S_2 = \{ \frac{1}{2}, 0{\color{red}\not}.\bar{9}, 1, 1.4, 2, 17 \} $
- WOW! That's a VERY nicely written answer. Great work. You only missed one little (somewhat tricky) detail. Can you guess what it is? MATH MAJORS: Can you help him? -pm
- Okay, answer above edited to account for the following:
- $ \frac{1}{9} = 0.\bar{1} $
- $ \frac{1}{9} * 9 = 0.\bar{9} $
- $ \frac{1}{9} * 9 = 1 $
- $ \therefore 0.\bar{9} = 1 $
- Instructor's comment: There you go! -pm
Answer 2
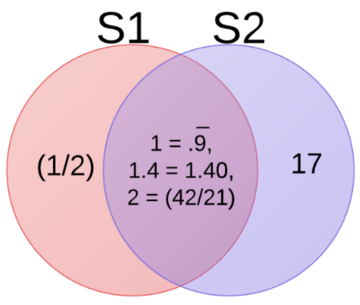
The union of S1 and S2 is all the elements in the Venn diagram: in S1, S2, and in both S1 and S2.
Answer 3
Write it here.

