| Line 1: | Line 1: | ||
[[Category:ECE301Spring2013JVK]] [[Category:ECE]] [[Category:ECE301]] [[Category:probability]] [[Category:problem solving]] | [[Category:ECE301Spring2013JVK]] [[Category:ECE]] [[Category:ECE301]] [[Category:probability]] [[Category:problem solving]] | ||
| − | 1. [[Category:LTI systems]] | + | 1. |
| + | |||
| + | [[Category:LTI systems]] | ||
Linear: <math>y[n]=x[n]+3x[n-1]</math> | Linear: <math>y[n]=x[n]+3x[n-1]</math> | ||
| Line 21: | Line 23: | ||
Time Invariant: <math>y[n]=x[n-2]^3</math> | Time Invariant: <math>y[n]=x[n-2]^3</math> | ||
| − | 2. [[Category:convolution]] | + | 2. |
| + | |||
| + | [[Category:convolution]] | ||
| + | |||
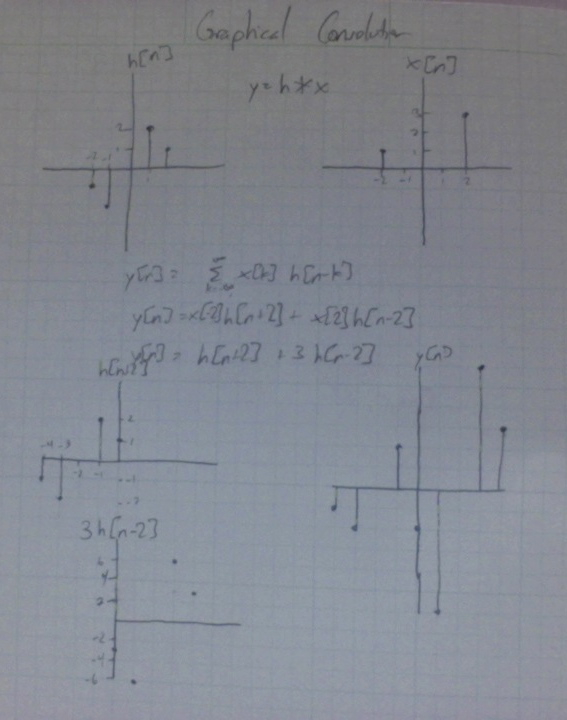
[[Image:Graphical_Convolution.jpg]] | [[Image:Graphical_Convolution.jpg]] | ||
| − | 3. [[Category:period]] | + | |
| + | 3. | ||
| + | |||
| + | [[Category:period]] | ||
| + | |||
<math>y(t)=cos(4t)</math> | <math>y(t)=cos(4t)</math> | ||
The period is <math>pi/2</math> | The period is <math>pi/2</math> | ||
[[Bonus_point_1_ECE301_Spring2013|Back to first bonus point opportunity, ECE301 Spring 2013]] | [[Bonus_point_1_ECE301_Spring2013|Back to first bonus point opportunity, ECE301 Spring 2013]] | ||
Latest revision as of 11:52, 11 February 2013
1.
Linear: $ y[n]=x[n]+3x[n-1] $ Non Linear: $ y[n]=x[n]^2+x[n] $
Causal: $ y[t]=(1/3)x[t] $ Non Causal: $ y[n]=x[n+5]+x[n-2] $
With Memory: $ y[n]=x[n-1]^2 $ Without Memory: $ y[n]=sin(x[n]) $
Invertible: $ y[t]=16x[t] $ Non Invertible: $ y[t]=|x[t]| $
Stable: $ y[n]=x[n^2]+x[n-1] $ Unstable: $ y[n]=n!x[n] $
Time Variant: $ y[n]=x[n]/(n^2+1) $ Time Invariant: $ y[n]=x[n-2]^3 $
3.
$ y(t)=cos(4t) $ The period is $ pi/2 $