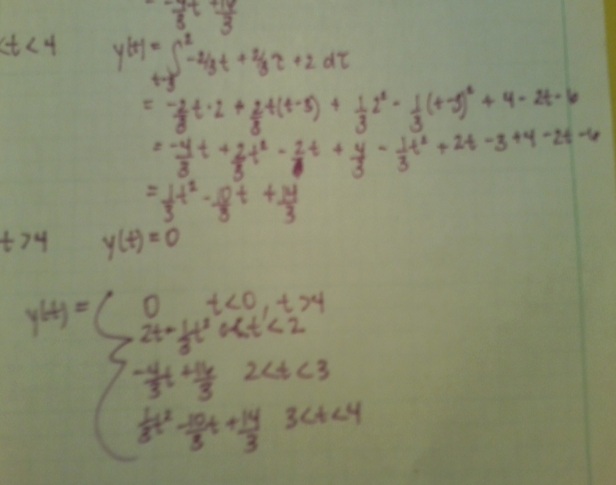| Line 5: | Line 5: | ||
Linear example <math>y[n] = 54x[n]</math>, <math>h[n] = 62x[n]</math>, <math>y[n] + h[n] = 54x[n] + 62x[n]</math> | Linear example <math>y[n] = 54x[n]</math>, <math>h[n] = 62x[n]</math>, <math>y[n] + h[n] = 54x[n] + 62x[n]</math> | ||
| + | |||
Non Linear example <math>y(t) =x^3(t)</math>, <math>h(t) = x^3(t)</math>, <math>y(t) + h(t) = (x(t)+x(t))^2</math> =\= <math>x^2(t) +x^2(t)</math> | Non Linear example <math>y(t) =x^3(t)</math>, <math>h(t) = x^3(t)</math>, <math>y(t) + h(t) = (x(t)+x(t))^2</math> =\= <math>x^2(t) +x^2(t)</math> | ||
| Line 21: | Line 22: | ||
Invertible example <math>y(t)=5x(t)</math> | Invertible example <math>y(t)=5x(t)</math> | ||
Nonivertible example <math>y(t)=x^4(t)</math> | Nonivertible example <math>y(t)=x^4(t)</math> | ||
| − | |||
Stable and Nonstable | Stable and Nonstable | ||
| Line 29: | Line 29: | ||
Time variant and Time invariant | Time variant and Time invariant | ||
| − | |||
Time variant example <math>y(t)=3tx(t)</math> | Time variant example <math>y(t)=3tx(t)</math> | ||
| Line 37: | Line 36: | ||
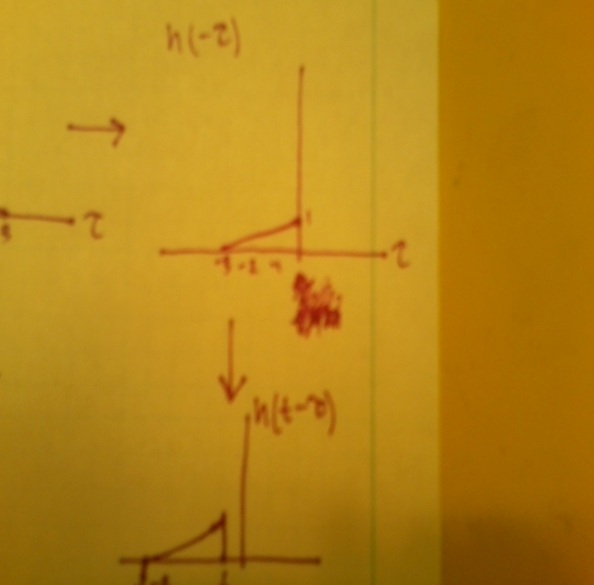
Part 1:[[Image:Convol_1.jpg]] | Part 1:[[Image:Convol_1.jpg]] | ||
| + | |||
Part 2:[[Image:Convol_2.jpg]] | Part 2:[[Image:Convol_2.jpg]] | ||
| + | |||
Part 3:[[Image:Convol_3.jpg]] | Part 3:[[Image:Convol_3.jpg]] | ||
| + | |||
Part 4:[[Image:Convol_4.jpg]] | Part 4:[[Image:Convol_4.jpg]] | ||
Revision as of 15:36, 10 February 2013
EXTRA CREDIT 1. Linear and Non Linear
Linear example $ y[n] = 54x[n] $, $ h[n] = 62x[n] $, $ y[n] + h[n] = 54x[n] + 62x[n] $
Non Linear example $ y(t) =x^3(t) $, $ h(t) = x^3(t) $, $ y(t) + h(t) = (x(t)+x(t))^2 $ =\= $ x^2(t) +x^2(t) $
Causal and Non Causal
Causal example $ y[n]=70x[n-1] $ Non Causal example $ y[n]=76x[n+1] $
Memory and Memoryless
Memory example $ y[n]=x[n]+x[n-1] $ Memoryless example $ y[n]=36x[n] $
Invertible and noninvertible
Invertible example $ y(t)=5x(t) $ Nonivertible example $ y(t)=x^4(t) $
Stable and Nonstable
Stable example $ y(t)=sin(3t) $ Nonstable example $ y(t)=4e^3x(t) $
Time variant and Time invariant
Time variant example $ y(t)=3tx(t) $ Time Invariant example $ y(t)=3x(t) $
2.