| Line 46: | Line 46: | ||
'''(b)''' [[Image:Ec1_partition.PNG | Visualization of Our Sample Space]] | '''(b)''' [[Image:Ec1_partition.PNG | Visualization of Our Sample Space]] | ||
| − | + | To solve '''b''', first we need to determine the probability that the first (red) pixel was sampled from image 1. Using the same method as in '''(a)''': | |
<math style='inline'>P(im1|R) = \frac{(\frac{1}{3})(.3)}{.5} = \frac{1}{5}</math> | <math style='inline'>P(im1|R) = \frac{(\frac{1}{3})(.3)}{.5} = \frac{1}{5}</math> | ||
| Line 53: | Line 53: | ||
'''(c)''' | '''(c)''' | ||
| + | For '''(b)''' and '''(c)''' it's important to realize that there is independence of subsequent pixel samplings within an image (intra-image, "locally"). | ||
However, if the image sampled from is not known, a sequence but dependence of subsequent pixel samplings between images (inter-image, "globally"). | However, if the image sampled from is not known, a sequence but dependence of subsequent pixel samplings between images (inter-image, "globally"). | ||
Revision as of 07:33, 27 January 2013
Pixel = 'Pic'ture 'El'ement
Above is an RGB image with a pixel color distribution of roughly the following:
red = 30% green = 10% blue = 60%
Therefore, if we were to randomly sample a pixel color from the image ('im1'), we would have the following probabilities of sampling each color:
P(R|im1) = .3 P(G|im1) = .1 P(B|im1) = .6
Given the following probabilities of two more RGB images with the same number of pixels as im1, solve (a), (b), and (c). (Note: we assume for this problem that pixels are sampled with replacement.)
P(R|im1) = .3 P(R|im2) = .8 P(R|im3) = .4 P(G|im1) = .1 P(G|im2) = .1 P(G|im3) = .2 } where R = red pixel sampled, etc, and im1 = pixel sampled is in image 1, etc. P(B|im1) = .6 P(B|im2) = .1 P(B|im3) = .4
(a) Assuming that we have an equal probability of sampling a pixel from each image, what is the probability that a sampled red
pixel came from image 3?
(b) Now, assume that after the first pixel is sampled, our remaining pixel samples must come from the same image as the first
pixel. Given that we first sampled a red pixel, then a green and blue, what is the probability that we have been sampling
from image 1? (Note that because pixels are not removed from the image after being sampled, the order of pixels sampled
after the first pixel does not matter.)
(c) Given the same {R,G,B} scenario as (b), and where pixels after the first must come from the same image, what is the
probability that our next (fourth) pixel sampled is red?
Solution
(a) We have been asked to find P(im3|R):
$ P(im3|R) = \frac{P(im3 \cap R)}{P(R)} $ from conditional probability $ = \frac{P(im3)P(R|im3)}{P(R)} $ from Bayes' rule
Because the numerators of the previous equation are both given, we are only left to find P(R). Since the sample space is partitioned into disjoint subsets im1, im2, and im3 (see graphic below), we can use the law of total probability: $ P(R) = \sum_{i=1}^{3} P(im_i)P(R|im_i) = \frac{1}{3}(.3 + .8 + .4) = .5 $
$ \therefore P(im3|R) = \frac{(\frac{1}{3})(.4)}{.5} $
(b)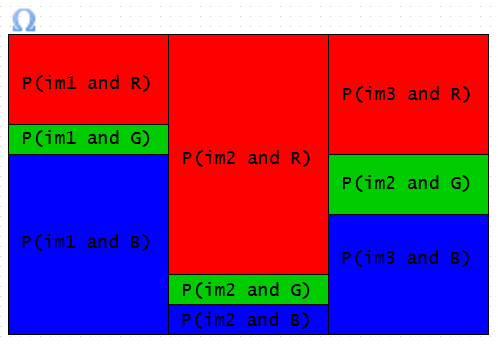
To solve b, first we need to determine the probability that the first (red) pixel was sampled from image 1. Using the same method as in (a):
$ P(im1|R) = \frac{(\frac{1}{3})(.3)}{.5} = \frac{1}{5} $
(c)
For (b) and (c) it's important to realize that there is independence of subsequent pixel samplings within an image (intra-image, "locally"). However, if the image sampled from is not known, a sequence but dependence of subsequent pixel samplings between images (inter-image, "globally").


