(New page: = Practice Problemon set operations = ---- Consider the following sets: <math> \begin{align} S_1 &= \left\{ \frac{1}{2}, 1, 1.4, 2 \right\}, \\ S_2 & = \l...) |
|||
| Line 23: | Line 23: | ||
=== Answer 1 === | === Answer 1 === | ||
| + | All elements in the following union are distinct, therefore the union is a set. | ||
| − | + | <math> S_1 \cup S_2 = \{ \frac{1}{2}, 0.\bar{9}, 1, 1.4, 2, 17 \} </math> | |
| + | |||
| + | [[Image:Lecture_3.PNG| 360x360px]] (<math class="inline"> S_1 \cup S_2</math> represented by colored region.) | ||
---- | ---- | ||
=== Answer 2 === | === Answer 2 === | ||
Revision as of 12:16, 11 January 2013
Contents
Practice Problemon set operations
Consider the following sets:
$ \begin{align} S_1 &= \left\{ \frac{1}{2}, 1, 1.4, 2 \right\}, \\ S_2 & = \left\{ 0.\bar{9}, 1.40, \frac{42}{21}, 17\right\}. \\ \end{align} $
Write $ S_1 \cup S_2 $ explicitely. Is $ S_1 \cup S_2 $ a set?
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
All elements in the following union are distinct, therefore the union is a set.
$ S_1 \cup S_2 = \{ \frac{1}{2}, 0.\bar{9}, 1, 1.4, 2, 17 \} $
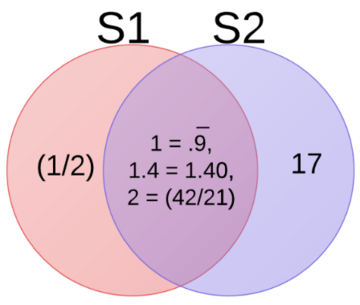
Answer 2
Write it here.
Answer 3
Write it here.

