| Line 224: | Line 224: | ||
| − | <font face="serif"><span style="font-size: 19px;"><math> | + | <font face="serif"><span style="font-size: 19px;"><math>\color{green} |
\text{therefore: } | \text{therefore: } | ||
</math></span></font> | </math></span></font> | ||
| Line 289: | Line 289: | ||
| − | <math> | + | <math>\color{green} |
| + | \text{ To make it more clear, the following form could be obtained:} | ||
| + | </math> | ||
| + | |||
| + | <math>\color{green} | ||
= \left\{\begin{matrix} | = \left\{\begin{matrix} | ||
\sqrt{1 - 4(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))^2}, &\text{ if }|r| \leq \frac{1}{2} | \sqrt{1 - 4(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))^2}, &\text{ if }|r| \leq \frac{1}{2} | ||
| Line 341: | Line 345: | ||
<font face="serif"><span style="font-size: 19px;"><math> | <font face="serif"><span style="font-size: 19px;"><math> | ||
| − | 3. \text{ Multiply step 2 by the filter } H(\rho) = |\rho| = f_c \left [ rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c}) \right ] | + | 3. \text{ Multiply step 2 by the filter } H(\rho) = |\rho| = f_c \left [ rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c}) \right ] |
</math></span></font> | </math></span></font> | ||
<font face="serif"><span style="font-size: 19px;"><math> | <font face="serif"><span style="font-size: 19px;"><math> | ||
| − | 4. \text{ Compute inverseFT of step 3 | + | 4. \text{ Compute inverseFT of step 3.} |
</math></span></font> | </math></span></font> | ||
| + | <math> \color{red} | ||
| + | \text{ This answer is not complete. We need the final step:} | ||
| + | </math> | ||
| − | <font face="serif"><span style="font-size: 19px;"><math> | + | |
| + | <font face="serif"><span style="font-size: 19px;"><math>\color{red} | ||
5. \text{ Back project } g_{\theta}(r) \text{ and get: } | 5. \text{ Back project } g_{\theta}(r) \text{ and get: } | ||
</math></span></font> | </math></span></font> | ||
| − | <font face="serif"><span style="font-size: 19px;"><math> | + | <font face="serif"><span style="font-size: 19px;"><math>\color{red} |
f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} | f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} | ||
</math></span></font> | </math></span></font> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
Revision as of 20:13, 2 August 2012
ECE Ph.D. Qualifying Exam in "Communication, Networks, Signal, and Image Processing" (CS)
Question 1, August 2011, Part 1
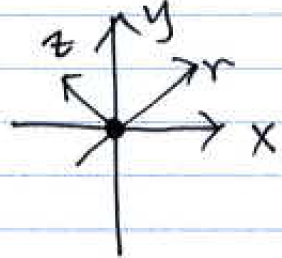
$ \color{blue}\text{Consider an image } f(x,y) \text{ with a forward projection} $
$ \color{blue} p_{\theta}(r) = \mathcal{FP}\left \{ f(x,y) \right \} $
$ \color{blue} = \int_{-\infty}^{\infty}{f \left ( r cos(\theta) - z sin(\theta),r sin(\theta) + z cos(\theta) \right )dz}. $
$ \color{blue} \text{Let } F(\mu,\nu) \text{ be the continuous-time Fourier transform of } f(x,y) \text{ given by} $
$ \color{blue} F(u,v) = \int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(x,y)e^{-j2\pi(ux,vy)}dx}dy} $
$ \color{blue} \text{and let } P_{\theta}(\rho) \text{ be the continuous-time Fourier transform of } p_{\theta}(r) \text{ given by} $
$ \color{blue} P_{\theta}(\rho) = \int_{-\infty}^{\infty}{p_{\theta}(r)e^{-j2\pi(\rho r)}dr}. $
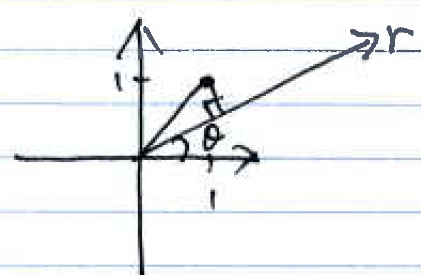
$ \color{blue}\text{a) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = \delta(x,y). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ = z \text{ when } \left\{\begin{matrix} r cos \theta - z sin \theta = 0 \\ r sin \theta + z cos \theta = 0 \end{matrix}\right. $
$ = \frac{r cos\theta}{sin \theta}, \theta > 0 $
$ {\color{red} \text{This answer is incorrect. The correct answer is as following:}} $
$ {\color{green} \text{Recall:}} $
$ {\color{green} \text{i) } \int_{-\infty}^{+\infty}{f(g(t)) \delta (t) dt} = f(g(t=0)) \int_{-\infty}^{+\infty}{\delta (t) dt} } $
$ {\color{green} \text{ii) } \int_{-\infty}^{+\infty}{\delta (\alpha t) dt} = \int_{-\infty}^{+\infty}{\delta (u) \frac{du}{|\alpha|}} = \frac{1}{|\alpha|} } $
$ {\color{green} \text{iii) } \delta() \text{ function is separable: } \delta(x,y) = \delta(x) \cdot \delta(y) } $
$ \color{green} \text{ Define } u = r cos\theta - z sin\theta $
$ \color{green} \Rightarrow dz = \frac{du}{|sin\theta|} $
$ \color{green} \text{ Now } $
$ \color{green} p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ \color{green} p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(g(u)) \delta(u) \frac{du}{|sin\theta|}} = \frac{\delta(u=0)}{|sin\theta|} $
$ \color{green} = \frac{\delta(\frac{r}{sin\theta})}{|sin\theta|} = \frac{|sin\theta|}{|sin\theta|} \delta(r) = \delta(r) $
$ \color{blue}\text{Solution 2:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ = \delta(r) $
$ {\color{green} \text{Here, the student uses the intuitive solution: in this case the answer does not depend on } \theta \text{, since the image just contains a peak at origin. } } $
$ \color{blue}\text{b) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = \delta(x-1,y-1). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{\delta(r cos\theta - z sin\theta - 1, r sin\theta + z cos \theta - 1) dz} $
$ = z \text{ when } \left\{\begin{matrix} r cos \theta - z sin \theta = 1 \\ r sin \theta + z cos \theta = 1 \end{matrix}\right. $
$ = \frac{r cos\theta - 1}{sin \theta}, \theta > 0 $
$ {\color{red} \text{This answer is incorrect. The correct answer is as following:}} $
$ \color{green} \text{ Similar to the solution 1 to part a) we define u: } u = r cos\theta - z sin\theta - 1 $
$ \color{green} \text{ Following the same logic as in part a) we obtain the final answer:} $
$ \color{green} p_{\theta}(r) = \delta(r - (cos\theta + sin \theta)) = \delta(r - \sqrt{2} cos (\theta - \frac{\pi}{4})) $
$ \color{blue}\text{Solution 2:} $
$ \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) $
$ = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $
$ = \delta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $
$ {\color{green} \text{Again, the student uses the intuitive solution: in this case the answer does depend on } \theta \text{, since the peak is shifted from the origin to the point } (1,1). } $
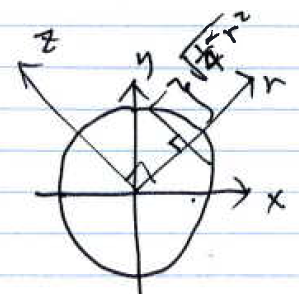
$ \color{blue}\text{c) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = rect \left(\sqrt[]{x^2+y^2} \right). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect(\sqrt{(r cos\theta - z sin\theta)^2 + (r sin\theta + z cos \theta)^2)} dz} $
$ \color{green} \text{Recall should be added:} $
$ \color{green} rect(t) = \left\{\begin{matrix} 1, for |t|\leq \frac{1}{2} \\ 0, otherwise \end{matrix}\right. $
$ \color{green} \text{therefore: } $
$ p_{\theta}(r) = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} $
$ = \left\{\begin{matrix} \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $
$ \color{blue}\text{Solution 2:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{f(r cos\theta - z sin\theta, r sin\theta + z cos \theta) dz} $
$ = \int_{-\sqrt{\frac{1}{4} - r^2}}^{\sqrt{\frac{1}{4} - r^2}}{1 dz} = \sqrt{1 - 4r^2}, \text{ if }|r| \leq \frac{1}{2} $
$ \text{ else } p_{\theta}(r) = 0 $
$ \color{blue}\text{d) Calculate the forward projection }p_{\theta}(r) \text{, for } f(x,y) = rect \left(\sqrt[]{(x-1)^2+(y-1)^2} \right). $
$ \color{blue}\text{Solution 1:} $
$ p_{\theta}(r) = \int_{-\infty}^{+\infty}{rect \left( \sqrt{(r cos\theta - z sin\theta - 1)^2 + (r sin\theta + z cos \theta - 1)^2} \right) dz} $
$ = \int_{-\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}^{\sqrt{\frac{1}{4} - (r - (cos\theta + sin\theta))^2}}{1 dz} $
$ = \left\{\begin{matrix} \sqrt{1 - 4(r - (cos\theta + sin\theta))^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $
$ \color{green} \text{ To make it more clear, the following form could be obtained:} $
$ \color{green} = \left\{\begin{matrix} \sqrt{1 - 4(r - \sqrt{2} cos (\theta - \frac{\pi}{4}))^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ otherwise} \end{matrix}\right. $
$ \color{blue}\text{Solution 2:} $
$ \tilde{p}_\theta(r) = p_{\theta}(r - \sqrt{1+1} cos(\theta - tan^{-1}(\frac{1}{1}))) $
$ = p_\theta(r - \sqrt{2} cos(\theta - \frac{\pi}{4})) $
$ \text{ where } p_\theta(r) = \left\{\begin{matrix} \sqrt{1 - 4r^2}, &\text{ if }|r| \leq \frac{1}{2} \\ 0, &\text{ else} \end{matrix}\right. $
$ {\color{green} \text{Here, the student uses the results from solutions to part b and c.} } $
$ \color{blue}\text{e) Describe in precise detail, the steps required to perform filtered back projection (FBP) reconstruction of } f(x,y). $
$ \color{blue}\text{Solution 1:} $
$ 1. \text{ Compute } \rho_{\theta}(r) $
$ 2. \text{ Compute FT of step 1.} $
$ 3. \text{ Multiply step 2 by the filter } H(\rho) = |\rho| = f_c \left [ rect(\frac{f}{2f_c}) - \Lambda(\frac{f}{f_c}) \right ] $
$ 4. \text{ Compute inverseFT of step 3.} $
$ \color{red} \text{ This answer is not complete. We need the final step:} $
$ \color{red} 5. \text{ Back project } g_{\theta}(r) \text{ and get: } $
$ \color{red} f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} $
$ \color{blue}\text{Solution 2:} $
$ 1. \text{ Measure the projections } \rho_{\theta}(r) \text{ at various angles} $
$ 2. \text{ Filter the projections } \rho_{\theta}(r) \text{ with } h(r) \text{, where } H(\rho) = |\rho| \text{ and get } g_{\theta}(r) $
$ 3. \text{ Back project } g_{\theta}(r) \text{ along } r = xcos\theta + ysin\theta \text{ and get } $
$ f(x,y) = \int_{0}^{\pi}{g_\theta(xcos\theta + ysin\theta)d\theta} $
"Communication, Networks, Signal, and Image Processing" (CS)- Question 5, August 2011
Go to
- Part 1: solutions and discussions
- Part 2: solutions and discussions