| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:honors project]] | ||
| + | [[Category:MA265]] | ||
| + | [[Category:linear algebra]] | ||
| + | |||
== On Asian Mathematics == | == On Asian Mathematics == | ||
| Line 18: | Line 22: | ||
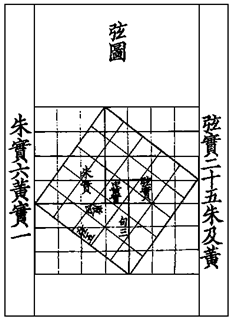
Unfortunately, no author is attributed with this monumental work of mathematics written circa 10th-2nd century BCE. The books format is not dissimilar to SAT practice-test book, as the entire content is in format of question, answer, and the method. What is implied by the “method”, however, is the depth of Asian mathematics, as it was evident that the Chinese scholars understood Gaussian method of solving linear equations (a small drawing of what appears to be matrix accompanies the solution) and Pythagorean Theorem, or as the Chinese scholars called it, Gongu rule. | Unfortunately, no author is attributed with this monumental work of mathematics written circa 10th-2nd century BCE. The books format is not dissimilar to SAT practice-test book, as the entire content is in format of question, answer, and the method. What is implied by the “method”, however, is the depth of Asian mathematics, as it was evident that the Chinese scholars understood Gaussian method of solving linear equations (a small drawing of what appears to be matrix accompanies the solution) and Pythagorean Theorem, or as the Chinese scholars called it, Gongu rule. | ||
Illsutration of the wordless Proof of Pythagoran Theorem | Illsutration of the wordless Proof of Pythagoran Theorem | ||
| − | + | ||
| + | [[Image:gongu.png]] | ||
The book also reveals the Chinese attitude for mathematics- that it is a tool for solving worldly problems. The contents of the books are organized under title of land surveing, taxes, agriculture & harvest- sorts of problems of applied mathematics rather than questions of abstract mathematics. | The book also reveals the Chinese attitude for mathematics- that it is a tool for solving worldly problems. The contents of the books are organized under title of land surveing, taxes, agriculture & harvest- sorts of problems of applied mathematics rather than questions of abstract mathematics. | ||
| Line 27: | Line 32: | ||
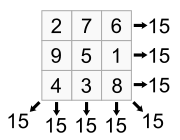
Perhaps I could best illustrate that reason for the lack of reason with one of the favored activity of Asian mathematicians – the construction of the magic squares (http://en.wikipedia.org/wiki/Magic_square). Magic squares are square arrangement of numbers is n x n dimension on which the sum of each elements in a column or row are all equal in value. An example of magic square is produced below | Perhaps I could best illustrate that reason for the lack of reason with one of the favored activity of Asian mathematicians – the construction of the magic squares (http://en.wikipedia.org/wiki/Magic_square). Magic squares are square arrangement of numbers is n x n dimension on which the sum of each elements in a column or row are all equal in value. An example of magic square is produced below | ||
| + | |||
| + | [[Image:180px-Magicsquareexample.svg.png]] | ||
Although the magic squares play little role in serious mathematics and is often introduced as mathematical puzzle, it was of great fascination for Asian mathematicians and had a legendary significance (it is told that one Chinese Emperor of a certain city beset by constant flooding found a ancient turtle with magic square engraved in its shell, and henceforth the city was “protected” from the flood). | Although the magic squares play little role in serious mathematics and is often introduced as mathematical puzzle, it was of great fascination for Asian mathematicians and had a legendary significance (it is told that one Chinese Emperor of a certain city beset by constant flooding found a ancient turtle with magic square engraved in its shell, and henceforth the city was “protected” from the flood). | ||
What I find interesting is not the magic squares themselves, but the receptions of those magic squares. Instead of devising algorithms for the construction of magic squares, as western mathematicians did, Chinese mathematicians simply marveled at the mystery of the magic squares. They interpreted it as another evidence of the mystery of the natural world, another evidence of its profound depth. The prevalent thought in the Asian philosophy (and I hope I am not authoring a new philosophy of Asian philosophy) was that the nature is supreme and that the human is only a small element in its astounding power and beauty. There was no need to understand nature- we are too little to understand nature- and that it is to our great blessing and pleasure to have the ability to perceive such beauty in nature. | What I find interesting is not the magic squares themselves, but the receptions of those magic squares. Instead of devising algorithms for the construction of magic squares, as western mathematicians did, Chinese mathematicians simply marveled at the mystery of the magic squares. They interpreted it as another evidence of the mystery of the natural world, another evidence of its profound depth. The prevalent thought in the Asian philosophy (and I hope I am not authoring a new philosophy of Asian philosophy) was that the nature is supreme and that the human is only a small element in its astounding power and beauty. There was no need to understand nature- we are too little to understand nature- and that it is to our great blessing and pleasure to have the ability to perceive such beauty in nature. | ||
| + | |||
| + | Hence, I interpret, the science of Asian culture is not concerned with the proof but the representation. It is most important that we discover and use science; explanation need not be presented since the new found truth must be the offspring of the nature, and thus is as it is. | ||
| + | |||
| + | So why no Asian mathematicians? It is probably not because ancient Asian cultures were disinclined to study mathematics but to study "mathematics" as we now define in modern sense - that art thirst for complete logical proof. | ||
| + | |||
| + | [[Honors_Project|Back to Daniel's Honor Project]] | ||
| + | |||
| + | [[2011_Fall_MA_265_Walther|Back to MA265 Fall 2011 Prof. Walther]] | ||
| + | |||
| + | [[MA265|Back to MA265]] | ||
Latest revision as of 10:46, 15 December 2011
On Asian Mathematics
On the occasions when the homage to great mathematicians of the past is sung, the gossiping of the greatest mathematician often follows (e.g. this forum). It is not a mathematical inquiry – nevertheless, it is an entertaining topic to have with fellow math person. The story of mathematics is weaved with persons of striking intelligence and insights, and although it is difficult to bestow the title of the greatest to a single individual, it is not so hard to compile a list of the brightest and the best-est. And it is, likewise, not difficult to note the dearth of Asian mathematicians among the best.
I am not particularly discouraged by this note- the age old stereotype of “Oh you Asian, so you must be good at mathematics” and the plethora of Asian mathematicians at the forefront of mathematics today would render the conclusion that Asians are inept in mathematics a premature one. I can also claim that the history of mathematics is really a history of western mathematics, that the glare of triumphs in western mathematics obscures the equivalent achievements Asian mathematics. Then, if an unbiased list of mathematics should be compiled by an omnipotent being who witnessed the history of mankind in every corner of the world, would Asians populate the list in proportion? Frankly, I am not so sure.
Asian Mathematics
First, when I talk of Asia, I talk not in strict terms of geography. Thus, I don’t plan to include India and Russia, although it would be impossible to talk about the general mathematical achievements without both countries.
What I do mean by “Asian mathematics” is the tradition of mathematics originating in China. And we begin our stories with the Asian mathematics book as foundational as Euclid’s Element- The Nine Chapters on the Mathematical Art (九章算术) http://ualr.edu/lasmoller/pythag.html
Unfortunately, no author is attributed with this monumental work of mathematics written circa 10th-2nd century BCE. The books format is not dissimilar to SAT practice-test book, as the entire content is in format of question, answer, and the method. What is implied by the “method”, however, is the depth of Asian mathematics, as it was evident that the Chinese scholars understood Gaussian method of solving linear equations (a small drawing of what appears to be matrix accompanies the solution) and Pythagorean Theorem, or as the Chinese scholars called it, Gongu rule. Illsutration of the wordless Proof of Pythagoran Theorem
The book also reveals the Chinese attitude for mathematics- that it is a tool for solving worldly problems. The contents of the books are organized under title of land surveing, taxes, agriculture & harvest- sorts of problems of applied mathematics rather than questions of abstract mathematics.
What is absent here is the rigorous study of mathematics as its own universe.
Why were Asian mathematicians, if there existed any (an individual whose sole concern was mathematics was a rare breed in Asian society), didn’t thirst for that logical completeness? That is, why do I see very little evidence of proof/justification in the mathematical works of the Asian mathematicians, an absence of that logical curiosity of why mathematical operations work in the way they do?
Perhaps I could best illustrate that reason for the lack of reason with one of the favored activity of Asian mathematicians – the construction of the magic squares (http://en.wikipedia.org/wiki/Magic_square). Magic squares are square arrangement of numbers is n x n dimension on which the sum of each elements in a column or row are all equal in value. An example of magic square is produced below
Although the magic squares play little role in serious mathematics and is often introduced as mathematical puzzle, it was of great fascination for Asian mathematicians and had a legendary significance (it is told that one Chinese Emperor of a certain city beset by constant flooding found a ancient turtle with magic square engraved in its shell, and henceforth the city was “protected” from the flood).
What I find interesting is not the magic squares themselves, but the receptions of those magic squares. Instead of devising algorithms for the construction of magic squares, as western mathematicians did, Chinese mathematicians simply marveled at the mystery of the magic squares. They interpreted it as another evidence of the mystery of the natural world, another evidence of its profound depth. The prevalent thought in the Asian philosophy (and I hope I am not authoring a new philosophy of Asian philosophy) was that the nature is supreme and that the human is only a small element in its astounding power and beauty. There was no need to understand nature- we are too little to understand nature- and that it is to our great blessing and pleasure to have the ability to perceive such beauty in nature.
Hence, I interpret, the science of Asian culture is not concerned with the proof but the representation. It is most important that we discover and use science; explanation need not be presented since the new found truth must be the offspring of the nature, and thus is as it is.
So why no Asian mathematicians? It is probably not because ancient Asian cultures were disinclined to study mathematics but to study "mathematics" as we now define in modern sense - that art thirst for complete logical proof.
Back to Daniel's Honor Project