| (6 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Question == | ==Question == | ||
| + | a) | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | y[m,n] =& -\frac{1}{8}x[m+1,n-1] + \frac{1}{2}x[m,n-1] - \frac{1}{8}x[m-1,n-1] \\ | ||
| + | & -\frac{1}{4}x[m+1,n] + x[m,n] -\frac{1}{4}x[m,n-1] \\ | ||
| + | & -\frac{1}{8}x[m+1,n+1] + \frac{1}{2}x[m,n+1] -\frac{1}{8}x[m-1,n+1] | ||
| + | \end{align}</math> | ||
| + | b) Yes. The coefficient matrix of h[m,n] can be written as product of two vectors. | ||
| + | <math> | ||
| + | \begin{pmatrix} | ||
| + | -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \\ | ||
| + | -\frac{1}{4} & 1 & -\frac{1}{4} \\ | ||
| + | -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} | ||
| + | \end{pmatrix} = | ||
| + | \begin{pmatrix} | ||
| + | \frac{1}{2} \\ | ||
| + | 1 \\ | ||
| + | \frac{1}{2} | ||
| + | \end{pmatrix} \cdot | ||
| + | \begin{pmatrix} | ||
| + | -\frac{1}{4} & 1 & -\frac{1}{4} | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | Therefore the filter can be separate into two 1-D filters. | ||
| + | |||
| + | <math>h_1[m] = -\frac{1}{4}\delta[m+1] + \delta[m] -\frac{1}{4}\delta[m-1]</math> | ||
| + | |||
| + | <math>h_2[n] = \frac{1}{2}\delta[n+1] + \delta[n] +\frac{1}{2}\delta[n-1]</math> | ||
| + | |||
| + | c) | ||
| + | |||
| + | <math>H_1(\mu) = DTFT\{h_1[m]\} = -\frac{1}{4}e^{-j\mu(-1)} + e^{-j\mu(0)} -\frac{1}{4}e^{-j\mu(1)} = 1-\frac{1}{2}cos\mu</math> | ||
| + | |||
| + | <math>H_2(\nu) = DTFT\{h_2[n]\} = \frac{1}{2}e^{-j\nu(-1)} + e^{-j\nu(0)} +\frac{1}{2}e^{-j\nu(1)} = 1+cos\nu</math> | ||
| + | |||
| + | Using the separability, | ||
| + | |||
| + | <math>H(\mu, \nu) = DSFT\{ h[m,n]\} = H_1(\mu)\cdot H_2(\nu) = (1-\frac{1}{2}cos\mu)(1+cos\nu)</math> | ||
| + | |||
| + | <math>H(\mu, 0) = 2(1-\frac{1}{2}cos\mu)</math> | ||
| + | |||
| + | [[Image:HW8Q1fig1.jpg]] | ||
| + | |||
| + | <math>H(0, \nu) = 2(1+cos\nu)</math> | ||
| + | |||
| + | [[Image:HW8Q1fig2.jpg]] | ||
| + | |||
| + | d) | ||
| + | |||
| + | <math>\begin{array}{cccccccccccc} | ||
| + | 0 & 0 & 0 & 0 & -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} & 0 & 0 & 0& 0 \\ | ||
| + | 0 & 0 & 0 & -\frac{1}{8} & \frac{1}{8} & \frac{10}{8} & \frac{1}{8} & -\frac{1}{8} & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & -\frac{1}{8} & \frac{1}{8} & \frac{7}{8} & \frac{10}{8} & \frac{7}{8} & \frac{1}{8} & -\frac{1}{8} & 0 & 0 \\ | ||
| + | 0 & -\frac{1}{8} & \frac{1}{8} & \frac{7}{8} & \frac{9}{8} & 1 & \frac{9}{8} & \frac{7}{8} & \frac{1}{8} & -\frac{1}{8} & 0 \\ | ||
| + | -\frac{1}{8} & \frac{1}{8} & \frac{7}{8} & \frac{9}{8} & 1 & 1 & 1 & \frac{9}{8} & \frac{7}{8} & \frac{1}{8} & -\frac{1}{8} \\ | ||
| + | -\frac{3}{8} & 1 & \frac{9}{8} & 1 & 1 & 1 & 1 & 1 & \frac{9}{8} & 1 & -\frac{3}{8} \\ | ||
| + | -\frac{1}{2} & \frac{3}{2} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \frac{3}{2} & -\frac{1}{2} \\ | ||
| + | -\frac{1}{2} & \frac{3}{2} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \frac{3}{2} & -\frac{1}{2} \\ | ||
| + | -\frac{1}{2} & \frac{3}{2} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \frac{3}{2} & -\frac{1}{2} \\ | ||
| + | -\frac{3}{8} & \frac{9}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{9}{8} & -\frac{3}{8} \\ | ||
| + | -\frac{1}{8} & \frac{3}{8} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{3}{8} & -\frac{1}{8} | ||
| + | \end{array}</math> | ||
---- | ---- | ||
Latest revision as of 12:42, 4 December 2011
Homework 8, ECE438, Fall 2011, Prof. Boutin
Question
a)
$ \begin{align} y[m,n] =& -\frac{1}{8}x[m+1,n-1] + \frac{1}{2}x[m,n-1] - \frac{1}{8}x[m-1,n-1] \\ & -\frac{1}{4}x[m+1,n] + x[m,n] -\frac{1}{4}x[m,n-1] \\ & -\frac{1}{8}x[m+1,n+1] + \frac{1}{2}x[m,n+1] -\frac{1}{8}x[m-1,n+1] \end{align} $
b) Yes. The coefficient matrix of h[m,n] can be written as product of two vectors.
$ \begin{pmatrix} -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \\ -\frac{1}{4} & 1 & -\frac{1}{4} \\ -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ 1 \\ \frac{1}{2} \end{pmatrix} \cdot \begin{pmatrix} -\frac{1}{4} & 1 & -\frac{1}{4} \end{pmatrix} $
Therefore the filter can be separate into two 1-D filters.
$ h_1[m] = -\frac{1}{4}\delta[m+1] + \delta[m] -\frac{1}{4}\delta[m-1] $
$ h_2[n] = \frac{1}{2}\delta[n+1] + \delta[n] +\frac{1}{2}\delta[n-1] $
c)
$ H_1(\mu) = DTFT\{h_1[m]\} = -\frac{1}{4}e^{-j\mu(-1)} + e^{-j\mu(0)} -\frac{1}{4}e^{-j\mu(1)} = 1-\frac{1}{2}cos\mu $
$ H_2(\nu) = DTFT\{h_2[n]\} = \frac{1}{2}e^{-j\nu(-1)} + e^{-j\nu(0)} +\frac{1}{2}e^{-j\nu(1)} = 1+cos\nu $
Using the separability,
$ H(\mu, \nu) = DSFT\{ h[m,n]\} = H_1(\mu)\cdot H_2(\nu) = (1-\frac{1}{2}cos\mu)(1+cos\nu) $
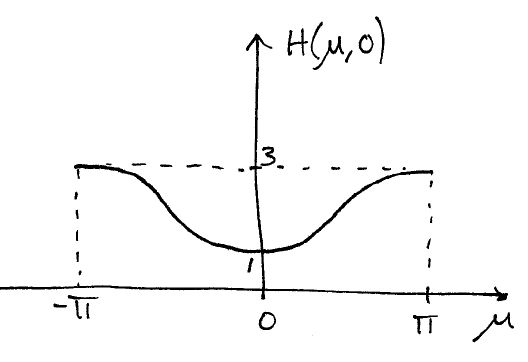
$ H(\mu, 0) = 2(1-\frac{1}{2}cos\mu) $
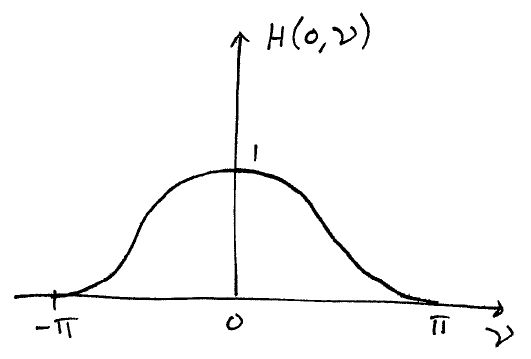
$ H(0, \nu) = 2(1+cos\nu) $
d)
$ \begin{array}{cccccccccccc} 0 & 0 & 0 & 0 & -\frac{1}{8} & \frac{1}{2} & -\frac{1}{8} & 0 & 0 & 0& 0 \\ 0 & 0 & 0 & -\frac{1}{8} & \frac{1}{8} & \frac{10}{8} & \frac{1}{8} & -\frac{1}{8} & 0 & 0 & 0 \\ 0 & 0 & -\frac{1}{8} & \frac{1}{8} & \frac{7}{8} & \frac{10}{8} & \frac{7}{8} & \frac{1}{8} & -\frac{1}{8} & 0 & 0 \\ 0 & -\frac{1}{8} & \frac{1}{8} & \frac{7}{8} & \frac{9}{8} & 1 & \frac{9}{8} & \frac{7}{8} & \frac{1}{8} & -\frac{1}{8} & 0 \\ -\frac{1}{8} & \frac{1}{8} & \frac{7}{8} & \frac{9}{8} & 1 & 1 & 1 & \frac{9}{8} & \frac{7}{8} & \frac{1}{8} & -\frac{1}{8} \\ -\frac{3}{8} & 1 & \frac{9}{8} & 1 & 1 & 1 & 1 & 1 & \frac{9}{8} & 1 & -\frac{3}{8} \\ -\frac{1}{2} & \frac{3}{2} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \frac{3}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{3}{2} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \frac{3}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{3}{2} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \frac{3}{2} & -\frac{1}{2} \\ -\frac{3}{8} & \frac{9}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{6}{8} & \frac{9}{8} & -\frac{3}{8} \\ -\frac{1}{8} & \frac{3}{8} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{3}{8} & -\frac{1}{8} \end{array} $
Back to Homework 8
Back to ECE 438 Fall 2011