(New page: Image:Monte_carlo_method.gif ) |
|||
| (5 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Image: | + | [[Category:ECE302Fall2008_ProfSanghavi]] |
| + | [[Category:probabilities]] | ||
| + | [[Category:ECE302]] | ||
| + | [[Category:problem solving]] | ||
| + | |||
| + | |||
| + | == Simple example showing how to Find Area of Circle ( THE COOL WAY!) == | ||
| + | |||
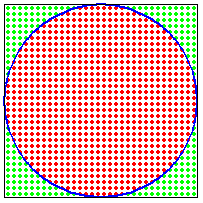
| + | Suppose we want to find the area of the circle given below. Here we can apply the '''Monte Carlo Method''' | ||
| + | |||
| + | <math>1</math> First we enclose the circle with a square. Suppose we find that the length of each side of square in this case is 2 units. Thus the radius of the circle is <br>1 unit. Hence we should look for an answer close to <math>\pi*r^{2}= \pi*1*1=3.14</math><br> | ||
| + | <math>2</math> Now first step is that we sample random points on the square. Now we calculate the number of points falling inside the circle and the number of points falling outside the circle.<br> | ||
| + | |||
| + | [[Image:Monte_carlo_method_ECE302Fall2008sanghavi.gif|Monte_carlo_method_ECE302Fall2008sanghavi.gif]] | ||
| + | |||
| + | Now, <math>p=\frac{no. of .points .inside .the .circle}{no. of .points .inside .the .circle. + no. of. points. outside. the. circle.}.</math> | ||
| + | |||
| + | Suppose we get 800 points in the circle and 200 points outside.<br> | ||
| + | Thus,<br> | ||
| + | |||
| + | <math>p=\frac{800}{800+200}.</math> | ||
| + | |||
| + | Therefore <math>p=\frac{800}{1000}=0.8.</math> | ||
| + | |||
| + | Hence, <math>the .area .of .circle = p * area. of .square</math><bR> | ||
| + | =<math>4 * 0.8</math><br> | ||
| + | =<math>3.2</math><br> | ||
| + | |||
| + | Here the value found is approximate and by taking more number of points we can get a more precise answer. | ||
| + | ---- | ||
| + | [[Main_Page_ECE302Fall2008sanghavi|Back to ECE302 Fall 2008 Prof. Sanghavi]] | ||
Latest revision as of 12:22, 22 November 2011
Simple example showing how to Find Area of Circle ( THE COOL WAY!)
Suppose we want to find the area of the circle given below. Here we can apply the Monte Carlo Method
$ 1 $ First we enclose the circle with a square. Suppose we find that the length of each side of square in this case is 2 units. Thus the radius of the circle is
1 unit. Hence we should look for an answer close to $ \pi*r^{2}= \pi*1*1=3.14 $
$ 2 $ Now first step is that we sample random points on the square. Now we calculate the number of points falling inside the circle and the number of points falling outside the circle.
Now, $ p=\frac{no. of .points .inside .the .circle}{no. of .points .inside .the .circle. + no. of. points. outside. the. circle.}. $
Suppose we get 800 points in the circle and 200 points outside.
Thus,
$ p=\frac{800}{800+200}. $
Therefore $ p=\frac{800}{1000}=0.8. $
Hence, $ the .area .of .circle = p * area. of .square $
=$ 4 * 0.8 $
=$ 3.2 $
Here the value found is approximate and by taking more number of points we can get a more precise answer.